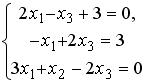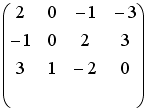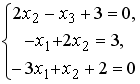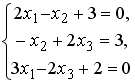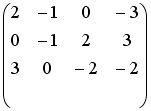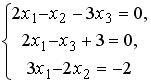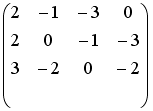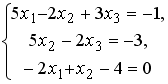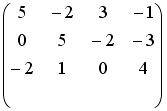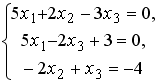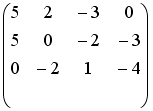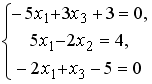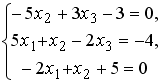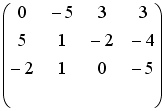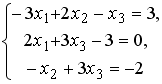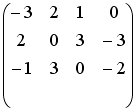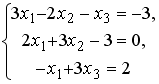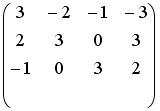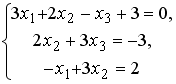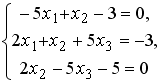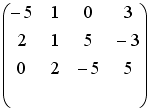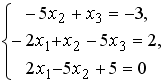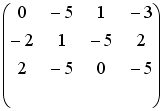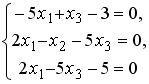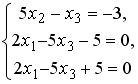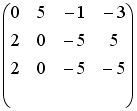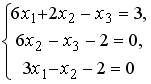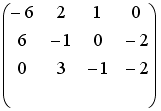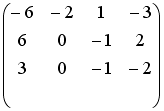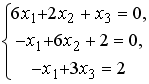- •Вычисление определителей
- •Матрицы: основные понятия и определения
- •Линейные операции над матрицами
- •Умножение матриц
- •Обратная матрица
- •Собственные значения матрицы
- •Системы линейных уравнений: основные понятия
- •Квадратичные формы
- •Функции: основные понятия и определения
- •Непрерывность функции. Точки разрыва
- •Производные первого порядка
- •Производные высших порядков
- •Асимптоты графика функции
- •Основные методы интегрирования
- •Свойства определенного интеграла
- •Приложения определенного интеграла
- •Основные понятия теории вероятностей
- •Теоремы сложения и умножения вероятностей
- •Полная вероятность. Формула байеса
- •Дискретная случайная величина
- •Характеристики вариационного ряда
- •Точечные оценки параметров распределения
- •Элементы корреляционного анализа
- •Проверка статистических гипотез
- •Линейное программирование
- •Транспортная задача
- •Сетевое планирование и управление
- •Марковские процессы
- •Функции полезности
- •Функции спроса и предложения
- •Производственные функции
- •Модели межотраслевого баланса
Обратная матрица
Установите
соответствие между двумя множествами
…
1.
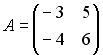 2.
2.
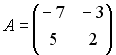 3.
3.
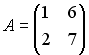
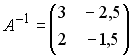 1
1
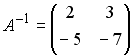 2
2
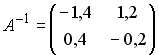 3
3
Установите
соответствие между двумя множествами
…
1.
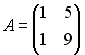 2.
2.
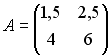 3.
3.
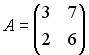
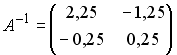 1
1
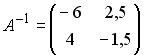 2
2
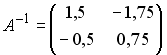 3
3
Установите
соответствие между двумя множествами
…
1.
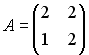 2.
2.
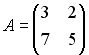 3.
3.

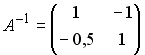 1
1
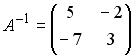 2
2
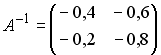 3
3
Установите
соответствие между двумя множествами
…
1.
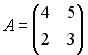 2.
2.
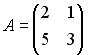 3.
3.
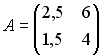
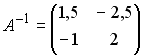 1
1
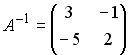 2
2
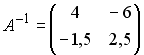 3
3
Установите
соответствие между двумя множествами
…
1.
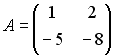 2.
2.
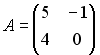 3.
3.
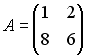
 1
1
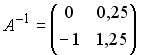 2
2
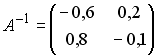 3
3
Обратная
матрица к матрице А= не
существует при
не
существует при![]() ,
равном … 0
,
равном … 0
Обратная
матрица к матрице А=
 не
существует при
,
равном … -13
не
существует при
,
равном … -13
Обратная
матрица к матрице А=
 не
существует при
,
равном
…
-11
не
существует при
,
равном
…
-11
Обратная
матрица к матрице А =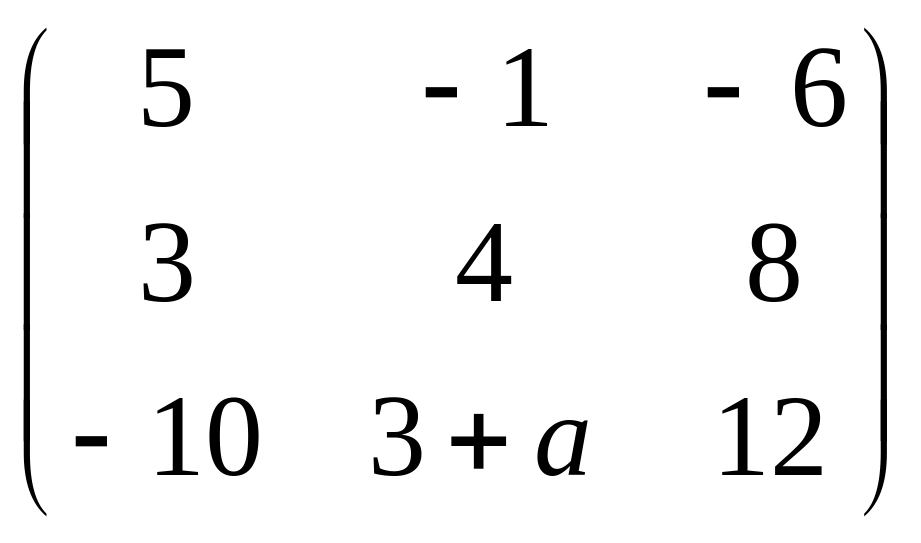 не
существует при
а ,
равном … -1
не
существует при
а ,
равном … -1
Обратная
матрица к матрице А = не
существует при
,
равном …-16
не
существует при
,
равном …-16
Собственные значения матрицы
Задано
характеристическое уравнение![]() матрицы.
Тогда матрица может иметь вид …
матрицы.
Тогда матрица может иметь вид …
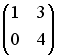
Задано
характеристическое уравнение![]() матрицы.
Тогда матрица может иметь вид …
матрицы.
Тогда матрица может иметь вид …
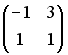
Вектор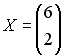 является
собственным вектором матрицы
является
собственным вектором матрицы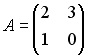 .
Тогда соответствующее собственное
значение равно … 3
.
Тогда соответствующее собственное
значение равно … 3
Вектор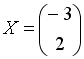 является
собственным вектором матрицы А,
соответствующий собственному значению
является
собственным вектором матрицы А,
соответствующий собственному значению![]() .
Тогда произведение AX равно
…
.
Тогда произведение AX равно
…
![]()
Вектор является
собственным вектором матрицы А,
соответствующий собственному значению
.
Тогда произведение AX равно
…
является
собственным вектором матрицы А,
соответствующий собственному значению
.
Тогда произведение AX равно
…
![]()
Системы линейных уравнений: основные понятия
Установите соответствие между системой линейных уравнений и ее расширенной матрицей.
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
Установите соответствие между системой линейных уравнений и ее расширенной матрицей. 1
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
Установите соответствие между системой линейных уравнений и ее расширенной матрицей.
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
Установите соответствие между системой линейных уравнений и ее расширенной матрицей.
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
Установите соответствие между системой линейных уравнений и ее расширенной матрицей.
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
Разность
между числом базисных и свободных
переменных системы уравнений равна
… 2
равна
… 2
Разность
между числом свободных и базисных
переменных системы уравнений![]() равна
…
2
равна
…
2
Разность
между числом свободных и базисных
переменных системы уравнений![]() равна
…
1
равна
…
1
Разность
между числом базисных и свободных
переменных системы уравнений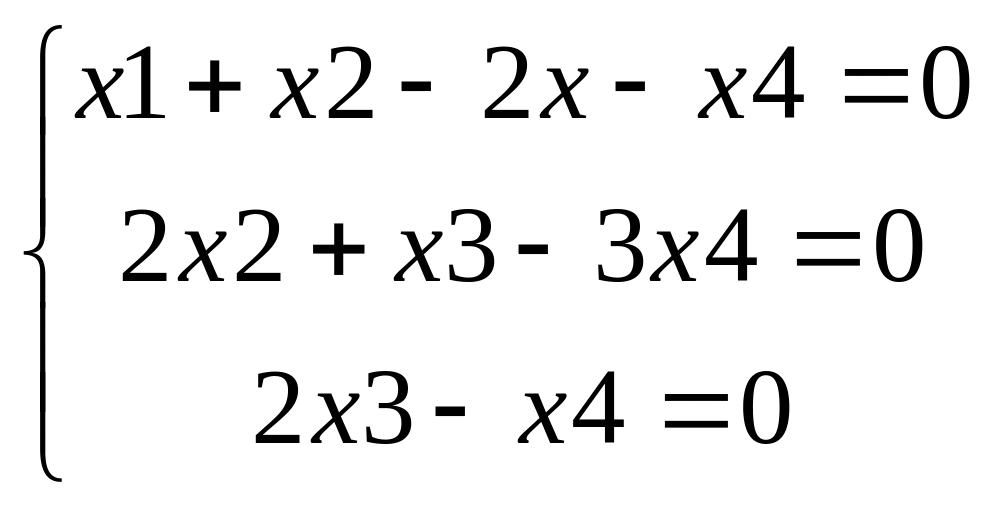 равна
… 2
равна
… 2
Разность между числом базисных и свободных переменных системы уравнений равна … 1
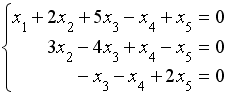
Дана
система линейных уравнений![]() .
Система не имеет решений при а
равном…
2
.
Система не имеет решений при а
равном…
2
Определитель
основной матрицы системы линейных
уравнений
![]() равен
… 15
равен
… 15
Определитель
основной матрицы системы линейных
уравнений![]() равен
… 8
равен
… 8
Если
(x0,y0) –
решение системы линейных уравнений
![]() ,
x0
-y0
тогда равно…
2,5
,
x0
-y0
тогда равно…
2,5
Определитель
основной матрицы системы линейных
уравнений![]() равен
… -
6
равен
… -
6