2. Найбільше та найменше значення функції

Функція задана і неперервна в замкненій та обмеженій області , досягає свого найбільшого і наймен­шого значень. У внутрішніх точках області диференційовна функція може набувати цих значень лише в точках локального екстремуму.

Алгоритм знаходження найбільшого і наймен­шого значень:

1) Знайти всі стаціонарні точки функції, які належать області , розв’язавши систему рівнянь і обчислити значення функції в цих точках.

2) Дослідити функцію на екстремум на межі області (знайти найбільше (найменше) значення функції на межі області ). Використовуючи рівняння межі, ця задача зводиться до знаходження абсолютного екстремуму функції однієї змінної.

3) Серед здобутих значень функції всередині і на межі області вибирають найбільше і найменше значення.

Приклад 3.

Знайти найбільше і найменше значення функції в області – трикутнику, обмеженому прямими х=0, у=0, х+у=6.

Знайдемо частинні похідні першого порядку:

Прирівнюючи похідні до нуля і скорочуючи їх на та (всередині трикутника ОАВ х≠0, у≠0) дістанемо систему рівнянь

Стаціонарна точка належить область D, тому обчислюємо значення .

Рівняннями сторін ОВ та ОА трикутника є х=0 та у=0, тому значення функції z=0 в усіх точках відрізків ОВ та ОА, зокрема z(0)= z(А)= z(В)=0.

Знайдемо стаціонарні точки на стороні АВ трикутника ОАВ. Рівняння цієї сторони у=6-х, тому z= .

Далі дістанемо:

Оскільки у=6-х, то ,

Знаходимо точки В(0;6) і С(4;2) і обчислюємо значення z(С)=-128.

Порівнюючи значення заданої функції в точках А, В, С, О, М, знаходимо найбільше й найменше значення:

Приклад 4.

Знайти екстремум функції

Знаходимо частинні похідні

Стаціонарні точки функції визначимо із системи:

Додаючи ці рівняння, знайдемо: звідки у= -х. Підставляючи у= -х в перше рівняння системи, дістанемо

тоді

Отже, функція має три стаціонарні точки: М (0;0), М ( ; - ), М (- ; ).

Знайдемо величину . Оскільки

то

Обчислимо величину в кожній стаціонарній точці: (М )=0, (М )= (М )=384>0, >0.

Таким чином, точки та - точки мінімуму. В цих точках

В точці М значення (М )=0, тому теорему 2 застосовувати не можна. Переконаємось, що в точці екстремум відсутній. Дійсно, якщо у=0, то <0 в околі точки М значення можуть бути як додатні, так і від’ємні, а це значить, що точка М не є екстремальною. Відзначимо, що інших екстремумів задана функція не має, оскільки, точки, в яких похідні і не існують, відсутні.

3. Умовний екстремум функції багатьох змінних

Нехай в області D задано функцію z = f (x, у) і лінію L, яка визначається рівнянням (х, у) = 0 та лежить в цій області.

Задача полягає в тому, щоб на лінії L знайти таку точку М (х; у), в якій значення функції f (х, у) є найбільшим або найменшим порівняно із значеннями цієї функції в інших точках лінії L. Такі точки М називають точками умовного екстремуму функції f (x, у) на лінії L. На відміну від звичайного екстремуму значення функ­ції в точці умовного екстремуму порівнюється із значеннями цієї функції не в усіх точках області D (чи - околу точки М), а лише в точках, які лежать на лінії L.

Назва «умовний екстремум» пов'язана з тим, що змінні х та у мають додаткову умову: (х, у) = 0.

Рівняння (х, у) = 0 називається рівнянням зв'язку; якщо це рівняння можна розв'язати відносно однієї змінної, наприклад у: у = (х), то підставляючи замість у значення (х) у функцію z = f (х, у), дістаємо функцію однієї змінної z = f (х, (х)). Оскіль­ки додаткова умова врахована, то задача знаходження умовного екс­тремуму зводиться до задачі на звичайний екстремум функції однієї змінної.

Проте не завжди можна розв'язати рівняння зв'язку відносно у чи х. Тоді розв'язують поставлену задачу так.

Розглянемо функцію z = f (х, у), де у= (х), як складену функ­цію. З необхідної умови екстремуму випливає, що в точках екстремуму

(1)

У цьому випадку означає похідну неявної функції, заданої рівнянням зв'язку (х, у) = 0:

, тому , тобто

Позначивши останні відношення через (- λ) (λ≠ 0) (знак мінус взято для зручності, а саме число λ може мати довільний знак), знайдемо, що в точці умовного екстремуму виконуються умови

, тобто

Отже, стаціонарні точки умовного екстремуму мають задовольняти систему рівнянь:

Аналізуючи цю систему, помічаємо, що знаходження умовного екстремуму функції z = f (х, у) звелось до знаходження звичайного екстремуму функції

Функція (3) називається функцією Лагранжа, а число – множ­ником Лагранжа.

Умови (2) є лише необхідними. Вони дають змогу знайти стаціо­нарні точки умовного екстремуму. З теореми 2 випливає, що характер умовного екстремуму (достатні умови) можна встановити за знаком диференціала другого порядку функції Лагранжа: якщо в стаціонарній точці >0

( < 0), то ця точка є точкою умов­ного мінімуму (максимуму).

Для функції U= f (х, у, z) з рівняннями зв'язку (х, у, z) = 0, (х, у, z) = 0 функція Лагранжа записується у вигляді

Стаціонарні точки умовного екстремуму знаходяться із системи рівнянь

а достатні умови існування умовного екстремуму в цих точках можна визначити за знаком диференціала .

Розглянутий метод можна поширити на дослідження умовного екстремуму функції довільного числа змінних.

Правило знаходження точок умовного екстремуму функції z = f (х, у):

1. Складаємо функцію Лагранжа:

2. Знаходимо стаціонарні точки із системи рівнянь:

3. Якщо в стаціонарній точці >0 ( < 0), то в цій точці функція має умовний мінімум (максимум).

Приклад:

Знайти найбільше і найменше значення функції z=xy, якщо x та у додатні і задовольняють рівняння зв’язку

Складемо функцію Лагранжа (3):

(

Користуючись системою (2), знаходимо стаціонарні точки цієї функції:

звідки х=2, у=1, =-2.

Отже, маємо одну стаціонарну точку М(2; 1; -2 ). Щоб визначити характер умовного екстремуму в цій точці, знайдемо за допомогою формули

другий диференціал функції Лагранжа при =-2:

Знайшовши з рівняння звязку dy(2;1)= , дістанемо

<0,

тому точка (2; 1) є точкою умовного максимуму функції z=xy. При цьому z =2.

Цей результат легко перевірити, знайшовши звичайний екстремум функції:

Приклад:

Знайти умовний екстремум функції z=x+y якщо х та у задовольняють рівняння зв'язку

Складемо функцію Лагранжа:

Користуючись системою (2), знаходимо стаціонарні точки цієї функції:

Із другого рівняння маємо , із третього . Підставляючи ці значення в перше рівняння, дістанемо Звідки

Отже, маємо дві стаеціонарні точки: М (- ; - ), М ( ; ). Далі необхідно зясувати, чи є знайдені точки точками екстремуму. Для цього обчислюємо значення другого диференціала функції у цих точках, вважаючи параметром. Знаходимо частинні похідні другого порядку

та диференціал другого порядку

при маємо >0, то в т. М (- ; - ) маємо умовний мінімум: z (- ; - ) = - - = - .

При <0, то в т. М ( ; ) маємо умовний максимум: z ( ; ) = + = .

Відповідь: z = - ,

z = .

Приклад:

Знайти умовний екстремум функції z=xy, якщо х та у задовольняють рівняння звчязку 4х-3у=12.

знаходимо стаціонарні точки:

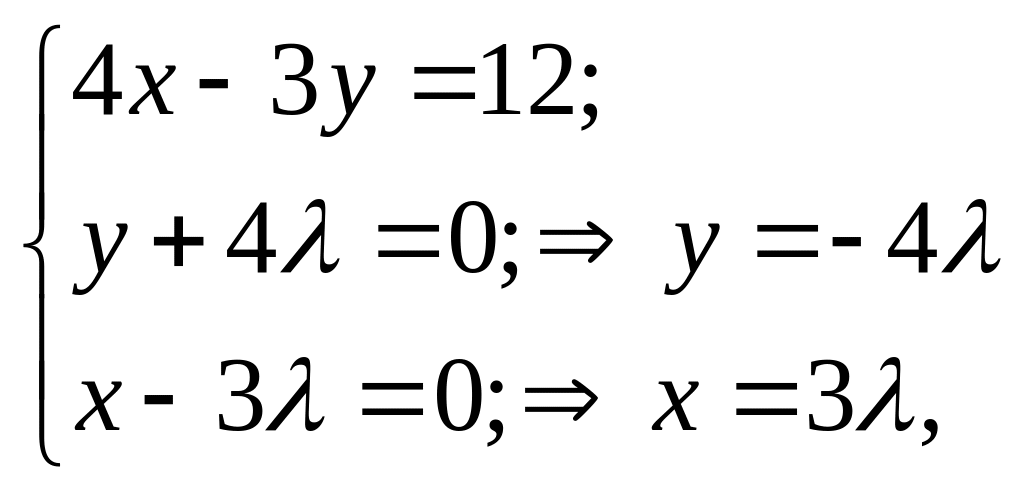
тоді 12 +12 =12; 24 =12; =

х=1,5; у=-2; z=-3.

Точка (1,5; -2; -3) – стаціонарна точка.

Знайдемо із рівняння звязку: , тоді

>0, тоді т.(1,5; -2; -3) є точкою умовного мінімуму функції z=xy.

z = -3.

ІІ спосіб

З рівняння звязку , тоді функція z=x·y при підстановці у буде функцією однієї змінної:

Знаходимо критичні точки першого роду:

z (1,5) = -3.

Можна визначити характер умовного екстремуму в точці 1,5 за допомогою частинної похідної другого порядку по змінній х: >0 х = 1,5 функція z=xy має умовний мінімум.

10