Лекція №13. Локальні екстремуми функції багатьох змінних. Умовний екстремум.

1. Локальні екстремуми функції двох змінних

2. Найбільше та найменше значення функції

3. Умовний екстремум

1. Локальні екстремуми функції двох змінних

Нехай функція z = f(х, у) визначена в області D, а точка D. Якщо існує окіл точки , який належить області D і для всіх відмінних від точок М цього околу виконується нерівність f (М)< f ( )(f (М) > f ( )), то точку називають точкою ло­кального максимуму (мінімуму) функції , а число – ло­кальним максимумом (мінімумом) цієї функції (рис. 1).

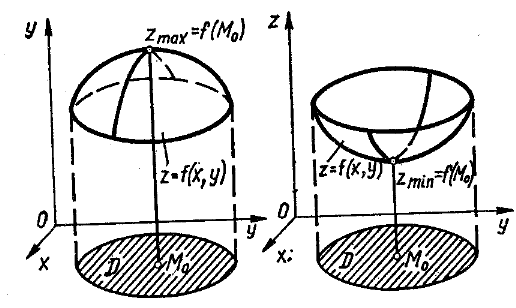
Рис. 1.

Точки максимуму та мінімуму функції називають її точками екстремуму.

Теорема 1 (необхідні умови екстремуму)

Якщо функція має в точці локальний екстремум, то в цій точці частин­ні похідні першого порядку по змінних х та у дорівнюють нулю або не існують.

Подібна теорема справедлива для функції n змінних. Точку , в якій частинні похідні першого порядку функції дорів­нюють нулю, тобто , називають стаціонарною точкою функції .

Стаціонарні точки та точки, в яких частинні похідні не існують, називаються критичними точками.

В задачах з практичним змістом, як правило, відомо, що функція має екстремум. Якщо така функція має лише одну критичну точку, то ця точка і буде точкою екстремуму.

Теорема 2 (достатні умови екстремуму)

Нехай в стаціонарній точці М (х ; у ) і деякому її околі функція має неперервні частинні похідні другого порядку. Якщо

>0,

то функція має в точці М екстремум, причому максимум при <0 і мінімум при >0. Якщо <0, то в точці М функція f (х, у) екстремуму не має.

Наслідок (другі достатні умови екстремуму)

Функція має мінімум в стаціонарній точці , якщо диференціал другого порядку в цій точці >0, і максимум – якщо <0.

Другі достатні умови екстремуму справедливі для функцій довільного числа змінних.

На основі теорем 1 і 2 дістанемо правило дослідження диференційовних функцій двох змінних на екстремум. Щоб знайти екстремум диференційовних функцій , необхідно:

1. Знайти стаціонарні точки функцій із системи рівнянь:

2. У кожній стаціонарній точці обчислити вираз , якщо >0, то – точка екстремуму функції, причому точка максимуму при <0 і мінімуму при >0; якщо <0, то точка (х ; у ) не є точкою екстремуму функції;

3. Обчислити значення функції в точках максимуму та мінімуму. Якщо =0, то ніякого висновок про характер стаціонарної точки зробити не можна і потрібне додаткове дослідження.

Приклад 1.

Знайти точки локального екстремуму функції

Знаходимо частинні похідні

Стаціонарні точки функції визначимо із системи:

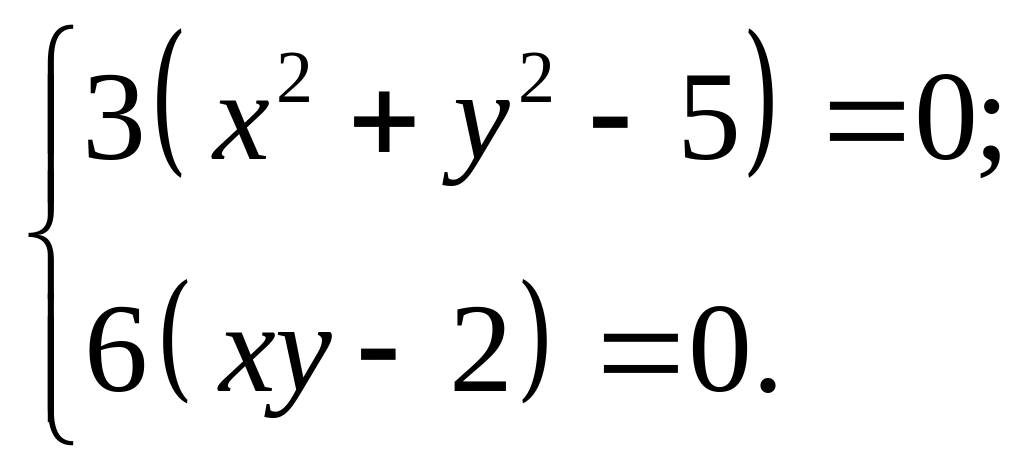
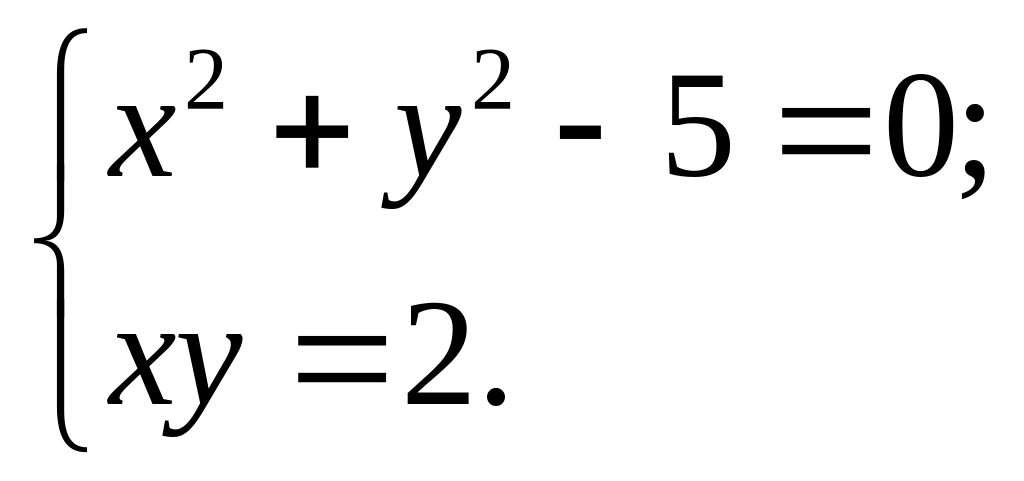
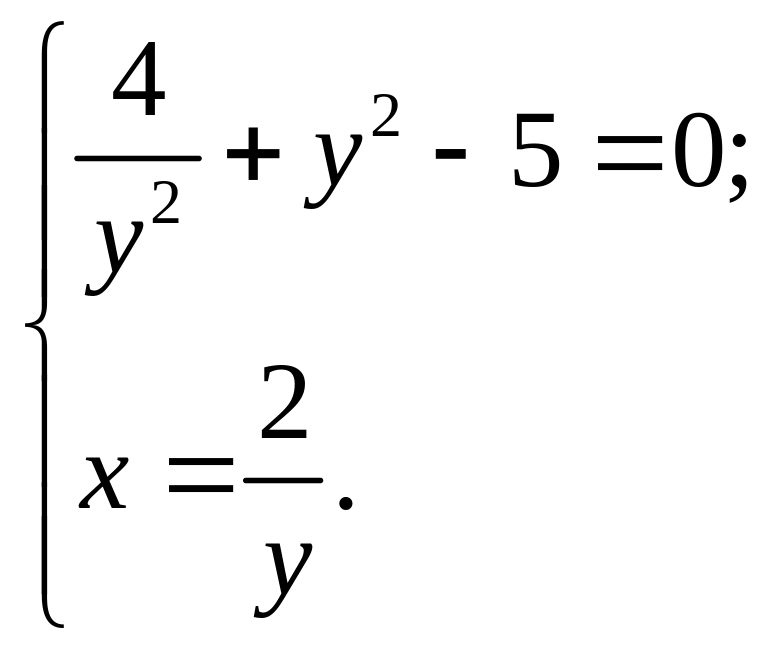
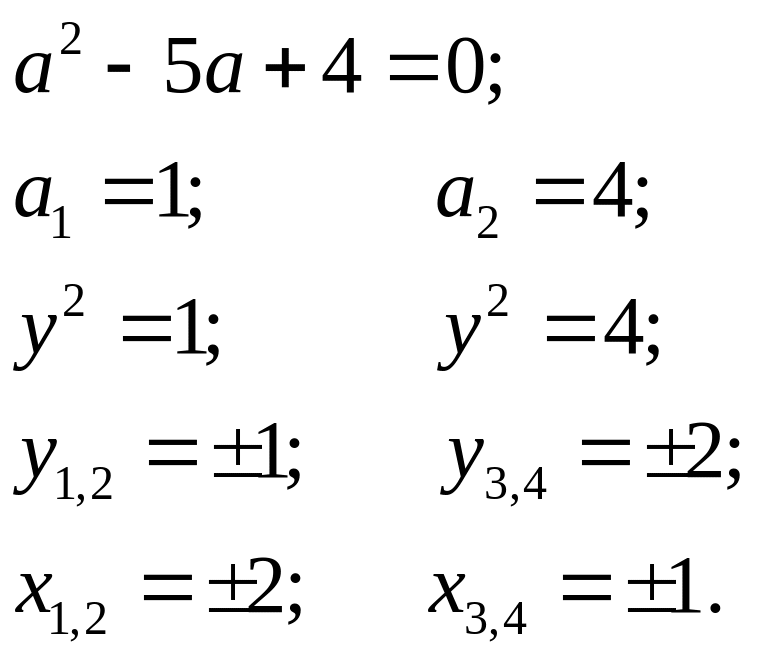
Отже, функція має 4 стаціонарні точки:

Знайдемо величину . Оскільки то

Обчислимо величину в кожній стаціонарній точці:

<0 – в т. немає екстремуму.

<0 – в т. немає екстремуму.

>0 – в т. функція має екстремум; >0, отже в т. функція має локальний мінімум:

>0 – в т. функція має екстремум; <0, отже в т. функція має локальний максимум:

Приклад 2.

Знайти стаціонарні точки функції .

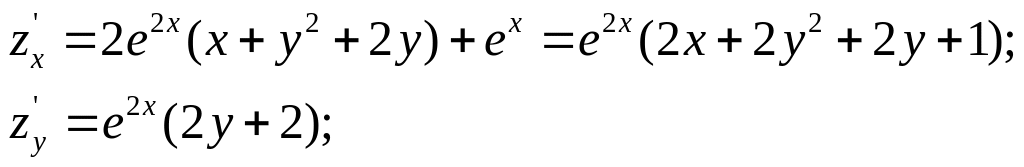
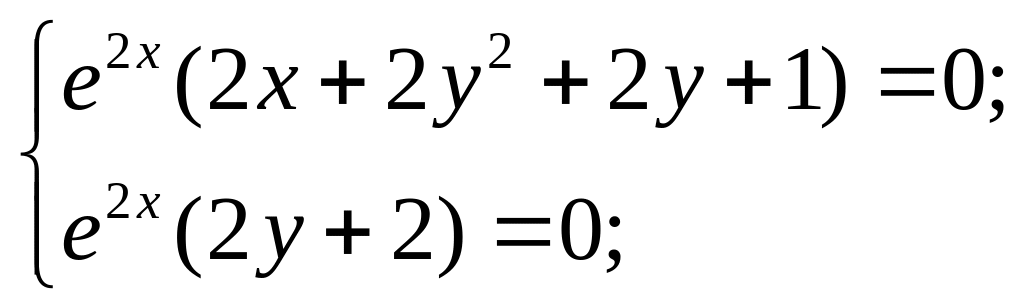
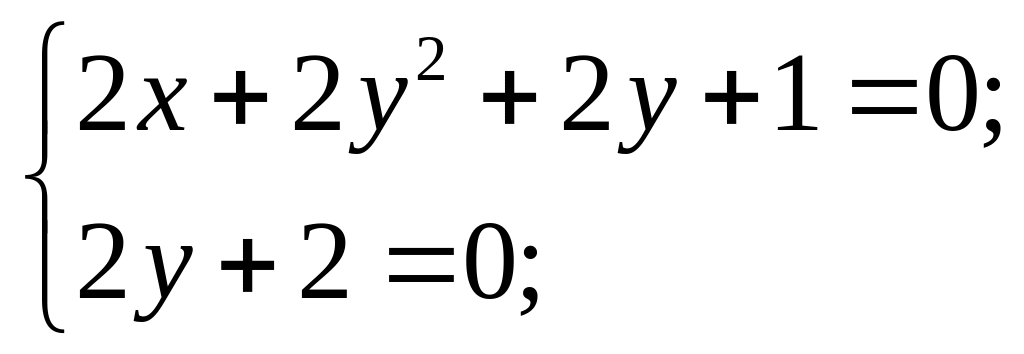
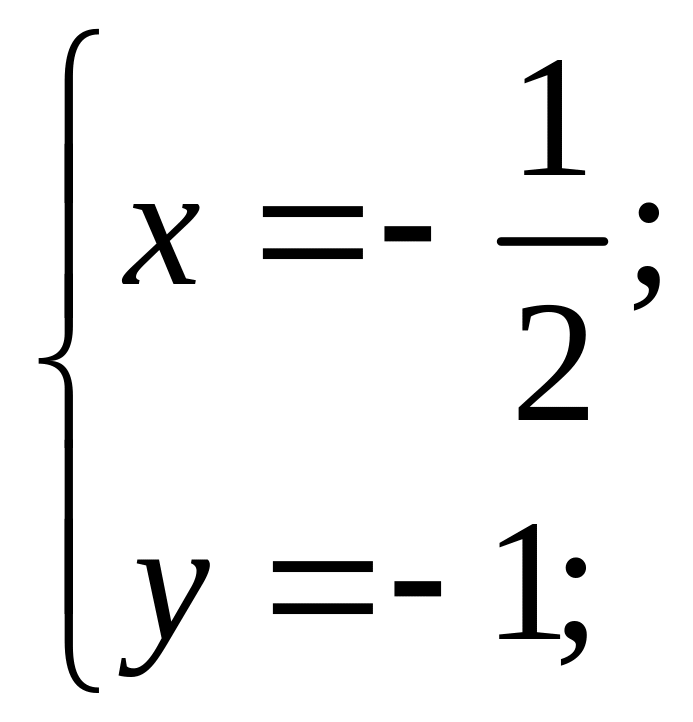
т. М(- ;-1) – стаціонарна точка.

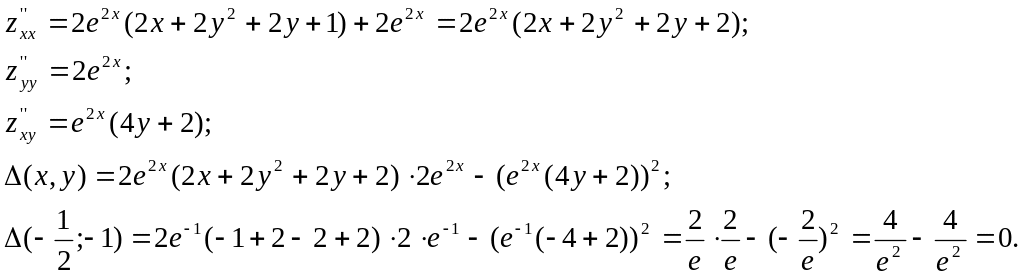
Так як =0, то ніякого висновку про характер стаціонарної точки зробити не можна і потрібне додаткове дослідження.