5) Електричне поле нескінченої рівномірно зарядженої прямої.

Р

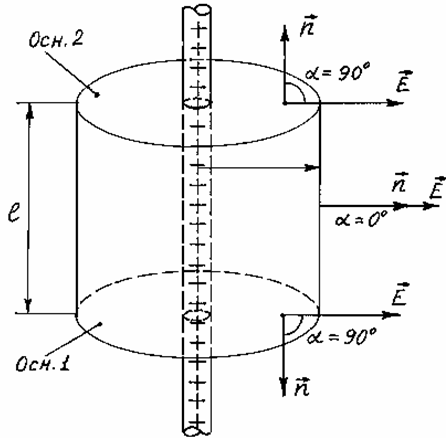
Рис.3.8.

озглянемо нескінченно довгу пряму, рівномірно заряджену електричним зарядом з лінійною густиною заряду . (3.42)

Л інійною густиною електричного заряду називається фізична величина рівна електричному зарядові одиниці довжини лінії вздовж якої він розподілений. У випадку рівномірного розподілу електричного заряду

(3.43)

де – електричний заряд який розподілений вздовж лінії довжиною .

В якості замкненої поверхні виберемо циліндричну поверхню радіусом r, висотою , вісь якої співпадає із зарядженою прямою, як зображено на рис. 3.8. Застосуємо теорему Остроградського-Гауса:

. (3.44)

І нтеграл по замкненій поверхні S запишемо як суму трьох інтегралів: по бічній поверхні, по першій і другій основах. Сумарний заряд, який охоплений поверхнею S, рівний зарядові на ділянці прямої довжиною . Із формули (3.43) цей заряд рівний:

. (3.45)

Підставимо (3.45) в (3.44):

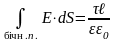
Оскільки і , то одержимо:

.

З міркувань симетрії випливає, що модуль Е є однаковим в усіх точках бічної поверхні. Тому винесемо Е за знак інтегралу:

. (3.46)

Інтеграл по бічній поверхні рівний площі цієї поверхні: (3.47)

Підставимо (3.47) у (3.46): (3.48)

З цієї формули випливає, що напруженість електричного поля, створеного нескінченою рівномірно зарядженою прямою обернено пропорційна до відстані між даною точкою простору і прямою. Ця формула справедлива також для нескінченого прямого рівномірно зарядженого циліндра.

6) Електричне поле нескінченної рівномірно зарядженої площини.

Розглянемо нескінченну площину рівномірно заряджену електричним зарядом з поверхневою густиною заряду : (3.49)

Поверхневою густиною електричного заряду називається фізична величина рівна електричному зарядові одиниці площі поверхні по якій розподілений заряд. У випадку рівномірного розподілу електричного заряду q по поверхні S поверхнева густина заряду рівна: (

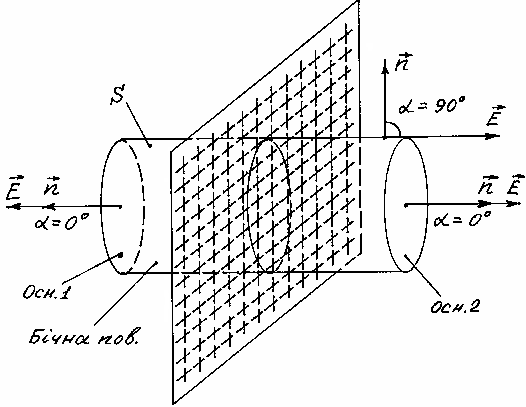
Рис.3.9

3.50)

В якості замкненої поверхні виберемо циліндричну поверхню з площею основи вісь якої перпендикулярна до зарядженої площини, як зображено на рис.3.9.

Застосуємо теорему Остроградського-Гауса (3.51)

Інтеграл по замкненій поверхні S запишемо як суму трьох інтегралів. Сумарний заряд, який охоплений поверхнею S рівний зарядові круга площею S_осн., який вирізує циліндр S на зарядженій площині. Виходячи із формули (3.50), цей заряд рівний (3.52)

Підставимо (3.52) в (3.51):

Оскільки і , то (3.53)

Інтеграли по поверхнях основ рівні: (3.54)

Підставимо (3.54) в (3.53): (3.55)

Із формули (3.55) випливає, що напруженість електричного поля, створеного нескінченною рівномірно зарядженою площиною не залежить від відстані до площини, тобто є однаковою в усіх точках простору по обидва боки від зарядженої площини. Це електричне поле є однорідним. Його силові лінії перпендикулярні до зарядженої площини.