Лабораторная работа №3 по ОТУ
.DOCЗадача 3.1 Определить характеристики в корневой и частотной областях последовательного соединения двух устойчивых апериодических звеньев первого порядка с параметрами: k1=1; T1=1c; k2=2; T2=2c. Рассчитать параметры k, T, ξ ПФ эквивалентного звена второго порядка, записанного в виде:
Рассмотрим два
устойчивых апериодических звена 1-го
порядка со следующими ПФ:
и
.
При последовательном соединении ПФ
эквивалентного звена
.
Отсюда получаем:
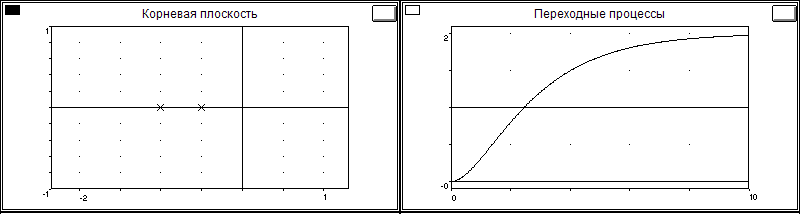
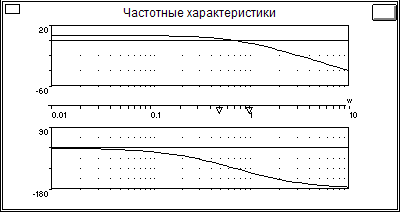
Частота среза: 0.6656
Время регулирования: 7.4258с;
Установившееся значение: 2.0000;
Полюсы: p1 = -1.000000; p2 = -0.500000;
Вопросы:
-
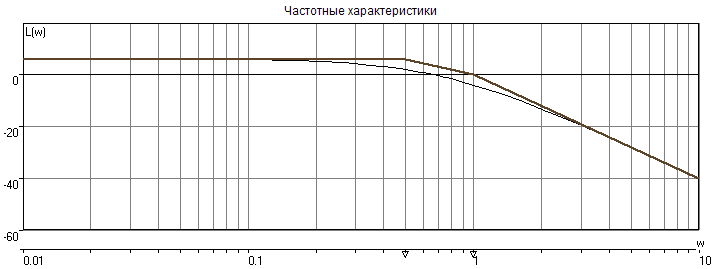
Какой вид имеет асимптотическая ЛАЧХ соединения?
асимптотическая ЛАЧХ соединения имеет вид ЛАЧХ апериодического звена 1-го порядка.
-
Как изменяется временная и частотная характеристики апериодического звена первого порядка при последовательном включении второго звена того же типа?
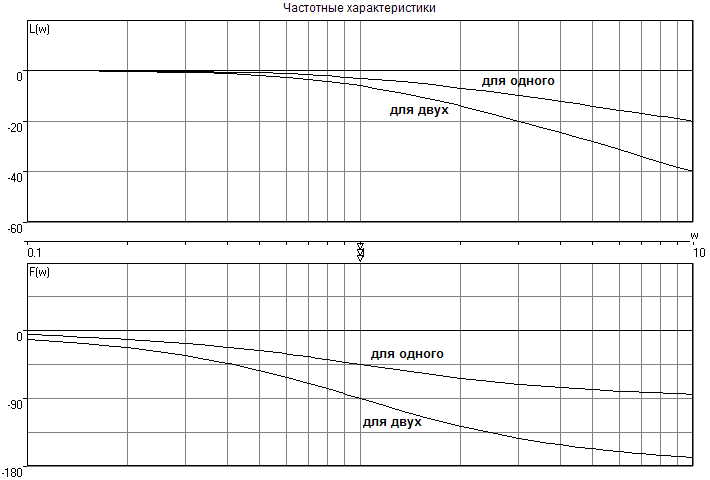
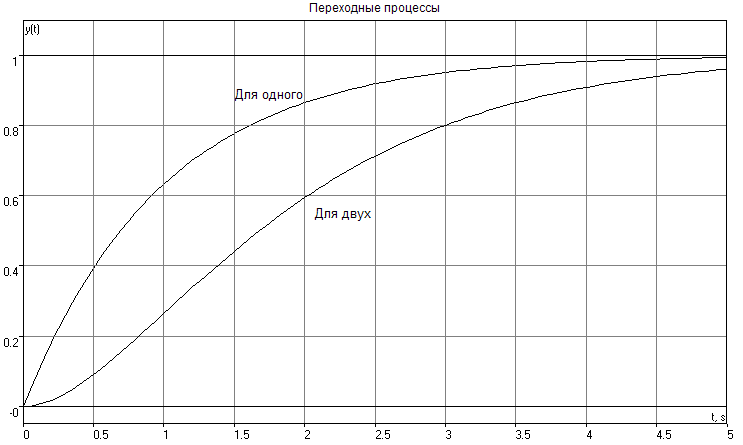
Изменение переходной характеристики
h(t) = h1(t) * h2(t) ;
изменение частотных характеристик
A(w) = A1(w) * A2(w)
Ф(w) = Ф1(w) + Ф2(w)
L(w) = L1(w) + L2(w)
|
Система |
из одного звена |
из двух звеньев |
|
Установившееся значение |
1.0000 |
1.0000 |
|
Время регулирования |
3.0100 с |
4.7492 с |
Вывод: при последовательном включении второго звена того же типа увеличится время регулирования.
-
Какое из двух звеньев оказывает основное влияние на длительность затухания переходного процесса?
Большее влияние на длительность затухания переходного процесса оказывает второе звено, так как коэффициент Т у него в 2 раза больше, а следовательно время регулирования также в 2 раза больше.
Задача 3.2 Определить
характеристики в корневой, временной
и частотной областях последовательного
соединения звеньев с ПФ 
При последовательном
соединении ПФ эквивалентного звена
.
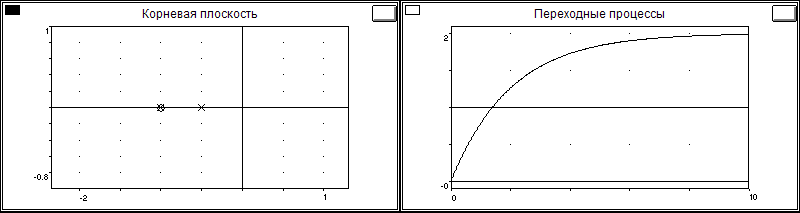
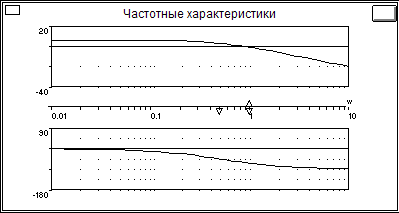
Частота среза: 0.8660
Установившееся значение: 2.0000;
Время регулирования: 6.0201 c;
Нули: z1 = -1.000000;
Полюсы: p1 = -1.000000; p2 = -0.500000;
Вопросы:
-
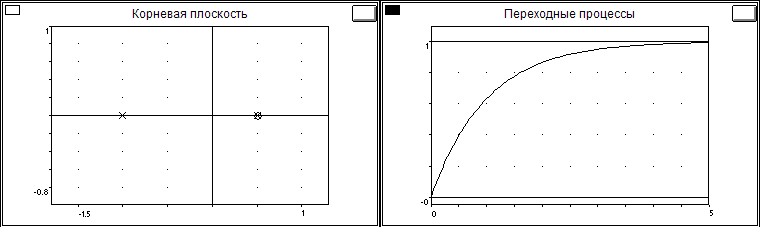
Какому звену соответствуют переходная и частотная характеристики соединения?
Исходя из ПФ
,
переходная и частотная характеристики
соединения соответствуют апериодическому
звену первого порядка с ПФ
,
k=2,
T=2.
Задача 3.3 Определить
характеристики в корневой, временной
и частотной областях звена с ПФ вида: 
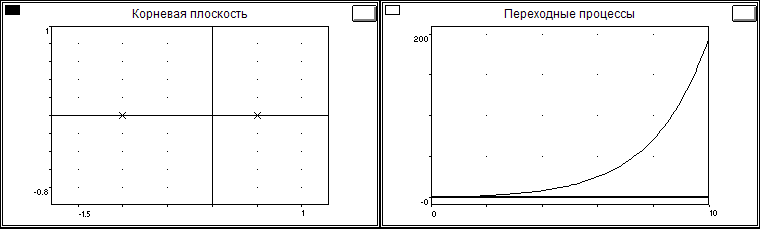
Частота среза: 0.6656
Полюсы: p1 = 0.500000; p2 = -1.000000;
Рассчитать ПФ W2(S) звена, последовательное включение которого со звеном W1(S) компенсирует его правый полюс.
Если
- не устойчивое звено, то система
последовательно включённых двух звеньев
будет устойчива при
,
следовательно ПФ
.
Вопросы:
-
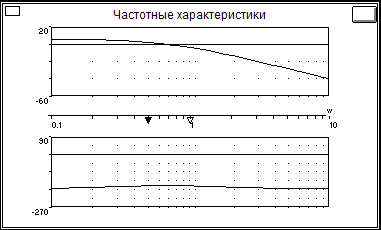
Как проявляются свойства неустойчивой части в последовательном соединении звеньев на характеристики соединения в целом с ПФ WЭ(S)?
Появляется полюс в правой полуплоскости, в результате образуется диполь.
-
Как отражается на характеристиках соединения с ПФ Wэ(s) в корневой, временной и частотной областях неполная компенсация неустойчивого полюса ПФ W1(s) ?
В корневой: левый полюс первого звена остался нескомпенсированным; во временной: переходная характеристика возрастает со временем; в частотной: изменение фазовой характеристики начинается с –π.
Задача 3.3 Найти ПФ Wi(S) типовых звеньев, параллельные соединения которых описываются эквивалентными ДУ вида:
Определить характеристики эквивалентных звеньев в корневой, временной и частотной областях. Построить их асимптотические ЛАЧХ. Пусть k=1, TИ=0.1, TД=0.01.
-
Wэ = k(1 +Tдs)
W1(s) = k W2(s) = kTдs
Характеристики эквивалентного соединения.
k = 10, Tд = 5
Корневая плоскость:
Переходная характеристика:
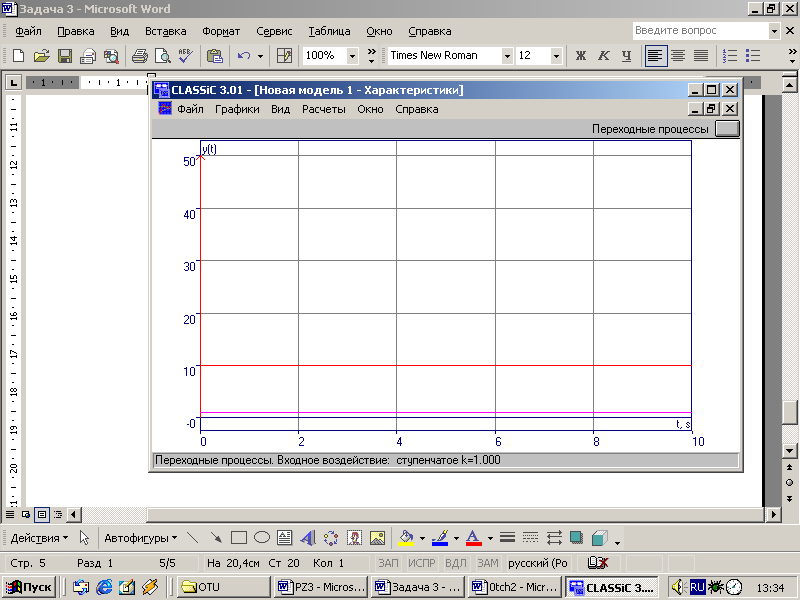
Частотные характеристики:
-
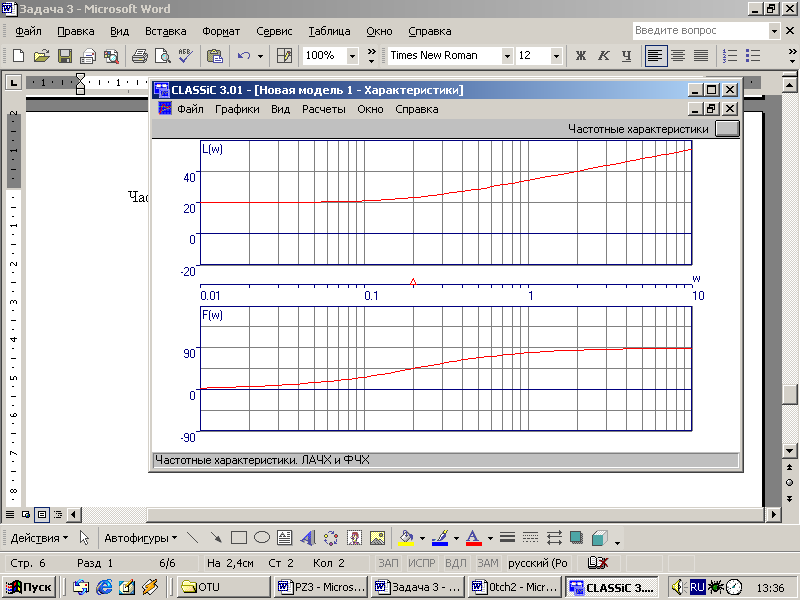
Wэ(s) = k + 1/(Tиs)
W1(s) = k
W2(s) = 1/(Tиs)
Характеристики эквивалентного соединения.
k = 10, Tи = 5
Корневая плоскость:
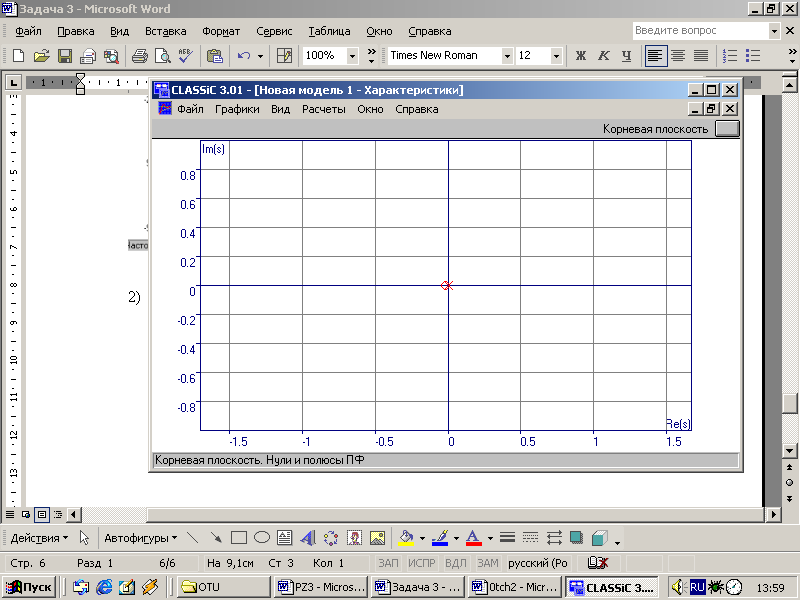
Переходная характеристика:
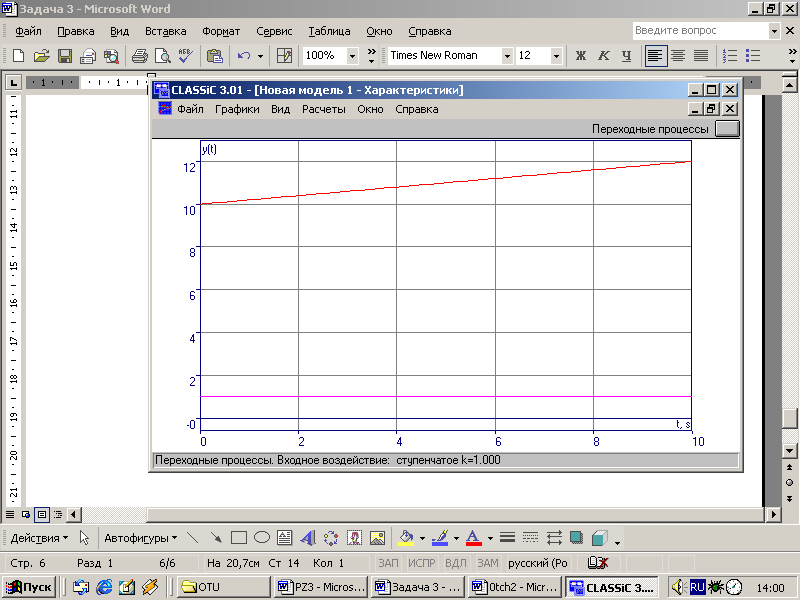
Частотные характеристики:
-
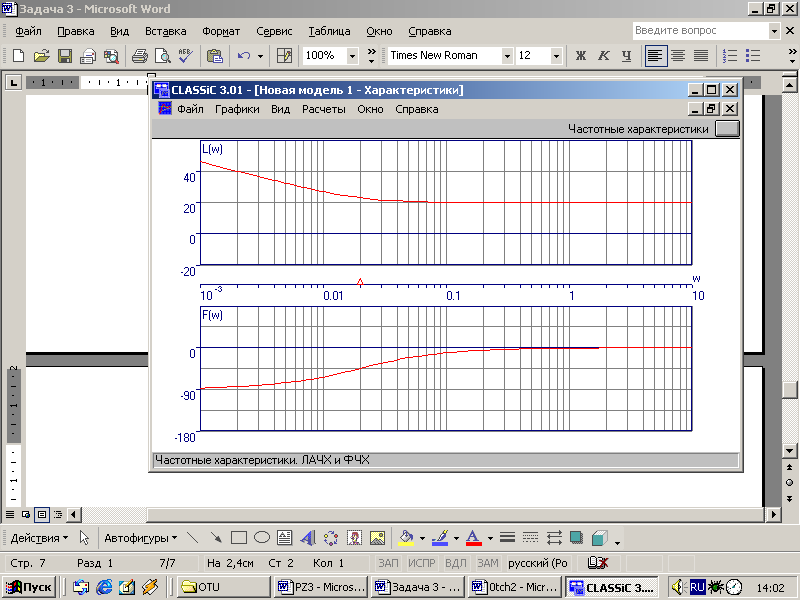
Wэ(s) = k + 1/(Tиs) + Tдs
W1 (s) = k
W2(s) = 1/(Tиs)
W3(s) = Tдs
Характеристики эквивалентного соединения.
k = 10, Tи = 5, Tд = 5
Корневая плоскость:
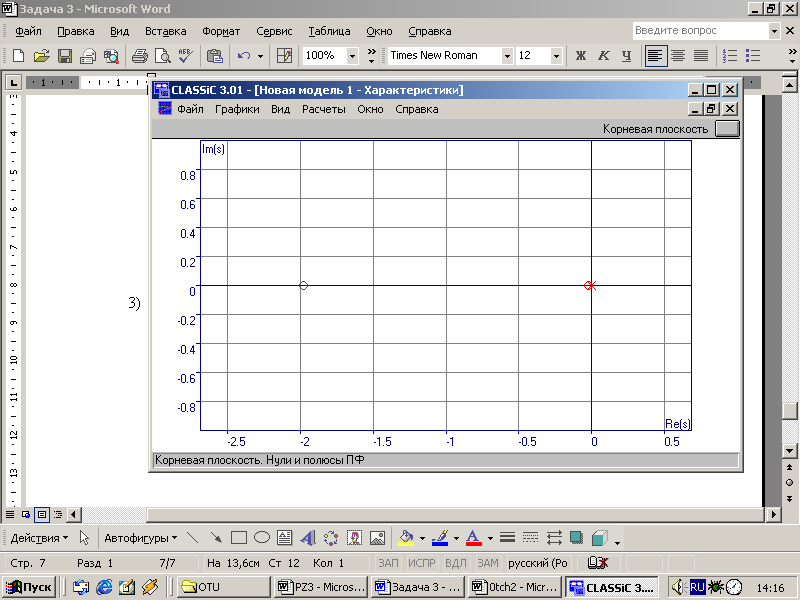
Переходная характеристика:
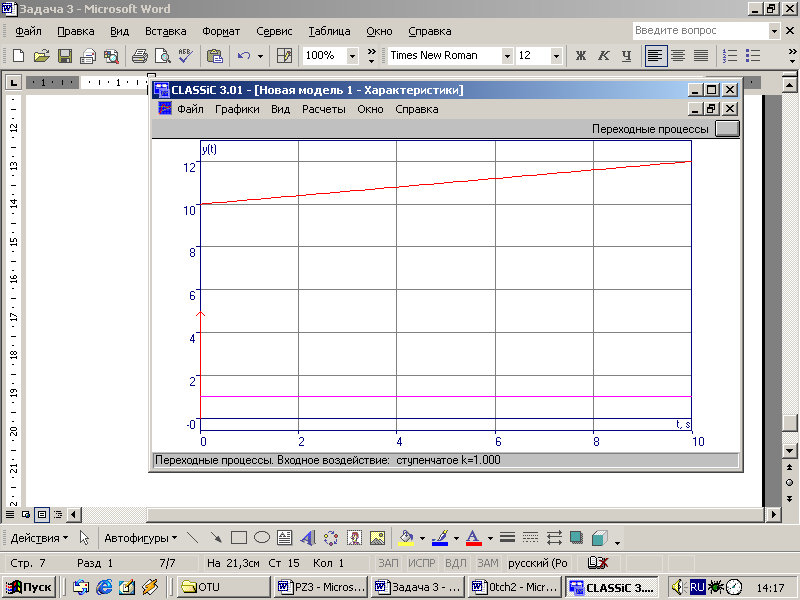
Частотные характеристики:
