
Лабораторная работа #31
.DOC
Министерство Науки и Образования Российской Федерации
Санкт-Петербургский государственный электротехнический университет
Кафедра МОЭВМ
Отчет
по лабораторной работе №3
по дисциплине
«Основы теории управления»
Выполнил: Свириденко С. В.
Ерёменок А. В.
Шульженко В.И.
Эмман П.А.
Группа: 3352
Факультет КТИ.
Проверил: Новожилов И. М.
Санкт-Петербург.
2006г.
Содержание
Исследование характеристик систем с обратной связью в корневой, временной и частотной областях. Устойчивость замкнутых систем с отрицательной обратной связью.
Основные сведения из теории
Обратные связи широко используются для целенаправленного изменения характеристик (свойств) физических элементов и систем управления. Целью этого занятия является изучение влияния обратной связи на характер собственных движений системы.
Рассмотрим замкнутую систему (рис. П 2.4а) с отрицательной обратной связью.
б)
а)


Рис.П2.4
Путем эквивалентного преобразования исходную структурную схему можно привести к виду, показанному на рис.П2.4б, где:
![]() (4)
(4)
Модель системы представляет собой последовательное соединение контура с единичной отрицательной обратной связью и звена с ПФ 1/W2(s). Предполагая, что материал третьего практического занятия уже освоен, здесь можно ограничиться рассмотрением характеристик только замкнутого контура (системы с единичной отрицательной обратной связью).
Как известно, характер собственных движений и устойчивость линейной динамической системы определяются только корнями ХП.
Для системы без контуров, т.е. только с последовательным или параллельным соединением звеньев, множество корней ее ХП является объединением подмножеств корней ХП этих звеньев. Если же соединения звеньев образуют контуры, то корни ХП в общем случае отличаются от корней ХП звеньев.
Запишем ПФ разомкнутой системы в виде:
![]() (5)
(5)
где k>0 - коэффициент передачи. Пусть степень полинома числителя не превышает степени полинома знаменателя.
ПФ замкнутой системы с единичной отрицательной обратной связью равна:
![]() (6)
(6)
а ее ХП определяется выражением:
![]() (7)
(7)
Корни ХП D(s) замкнутой системы в общем случае могут значительно отличаться от корней ХП D0(s) разомкнутой системы, причем, как это видно из (7), чем выше усиление контура (чем больше коэффициент передачи k), тем больше будет это отличие.
Отдельные корни ХП D0(s), число которых равно числу корней полинома D(s), после замыкания системы перемещаются на комплексной плоскости по-разному. Подвижность каждого корня зависит от усиления контура на частоте, равной модулю этого корня и от наличия близкого нуля ПФ W0(s). Здесь можно выделить следующие две группы корней ХП D(s):
- корни, приближенно равные тем нулям ПФ W0(s) разомкнутой системы (если такие нули, т.е. корни полинома B0(s) имеются), модули которых принадлежат области частот, где усиление контура велико, т.е.
![]()
- корни, приближенно равные тем полюсам ПФ W0(s) разомкнутой системы (корням ХП D0(s)), модули которых принадлежат области частот, где усиление контура мало, т.е.
W0(j)<0.1, L0()< -20дБ.
Если полиномы
![]() ПФ разомкнутой системы имеют нетривиальный
общий делитель, т.е. имеются нули ПФ
W0(s),
совпадающие с ее полюсами (диполи), то
среди полюсов ПФ (s)
будут полюсы, в точности равные этим
нулям. Т.е. при замыкании системы такие
полюсы ПФ W0(s)
остаются неподвижными.
ПФ разомкнутой системы имеют нетривиальный
общий делитель, т.е. имеются нули ПФ
W0(s),
совпадающие с ее полюсами (диполи), то
среди полюсов ПФ (s)
будут полюсы, в точности равные этим
нулям. Т.е. при замыкании системы такие
полюсы ПФ W0(s)
остаются неподвижными.
Как известно, общим условием устойчивости линейной системы (затухания собственных движений) является отрицательность действительных частей всех корней ее ХП. Необходимым условием является положительность всех коэффициентов ХП (для систем первого и второго порядков это условие является и достаточным).
Для исследования устойчивости замкнутых систем, порядок ХП D(s) которых n>2, используются алгебраические или частотные критерии.
Так, например, алгебраический критерий Гурвица для систем третьего порядка с ХП
D(s) = d3 s3 + d2 s2 + d1 s +d0 ,
определяет дополнительное условие устойчивости в виде неравенства:
d1d2 > d0d3 .
Если в этом выражении поставить знак равенства, то получим условие, при котором система находится на границе устойчивости (например, значение k = kкр при котором ХП (7) имеет пару чисто мнимых корней).
Для исследования устойчивости замкнутых систем можно также использовать частотный критерий Найквиста.
Задача 5.1. Для системы с единичной отрицательной обратной связью и ПФ прямого пути, равной
W0(s) = k/s
показать положение корня ХП D(s) на комплексной плоскости при различных значениях коэффициента передачи k 0.
Ответить на вопросы:
-
Какой вид имеет траектория корня системы при изменении k?
 k=2
k=2
 k=10
k=10
 k=50
k=50
-
Как изменяются переходная и частотные характеристики системы при увеличении k?
 k=2
k=2
 k=10
k=10
 k=50
k=50
Задача 5.2. Для системы из задачи 5.1 с ПФ вида
![]()
построить корневой годограф при изменении k от нуля до бесконечности.
Привести ПФ замкнутой системы к типовому виду, используемому в задаче 1.6, определить параметры T, этой ПФ для k = 10, T1 = 1 с.
![]()
Ответить на вопросы:
-
Как будут располагаться на комплексной плоскости корни ХП D(s) при k < 0?
-
Как изменяется переходная характеристика замкнутой системы при изменении коэффициента k в диапазонах 0 < k < ?
 k=2
k=2
 k=10
k=10
 k=50
k=50
Задача 5.3.
Для той же системы при ПФ в
![]() разомкнутом
состоянии равной
разомкнутом
состоянии равной

построить траекторию корней при изменении k. Определить критическое значение kкр, при котором замкнутая система находится на границе устойчивости. Исследовать временные и частотные характеристики замкнутой системы при k = kкр; k = 0.8kкр; k = 0.5kкр.
Корневые траектории:
 k=1.5
k=1.5
 k=1.2
k=1.2
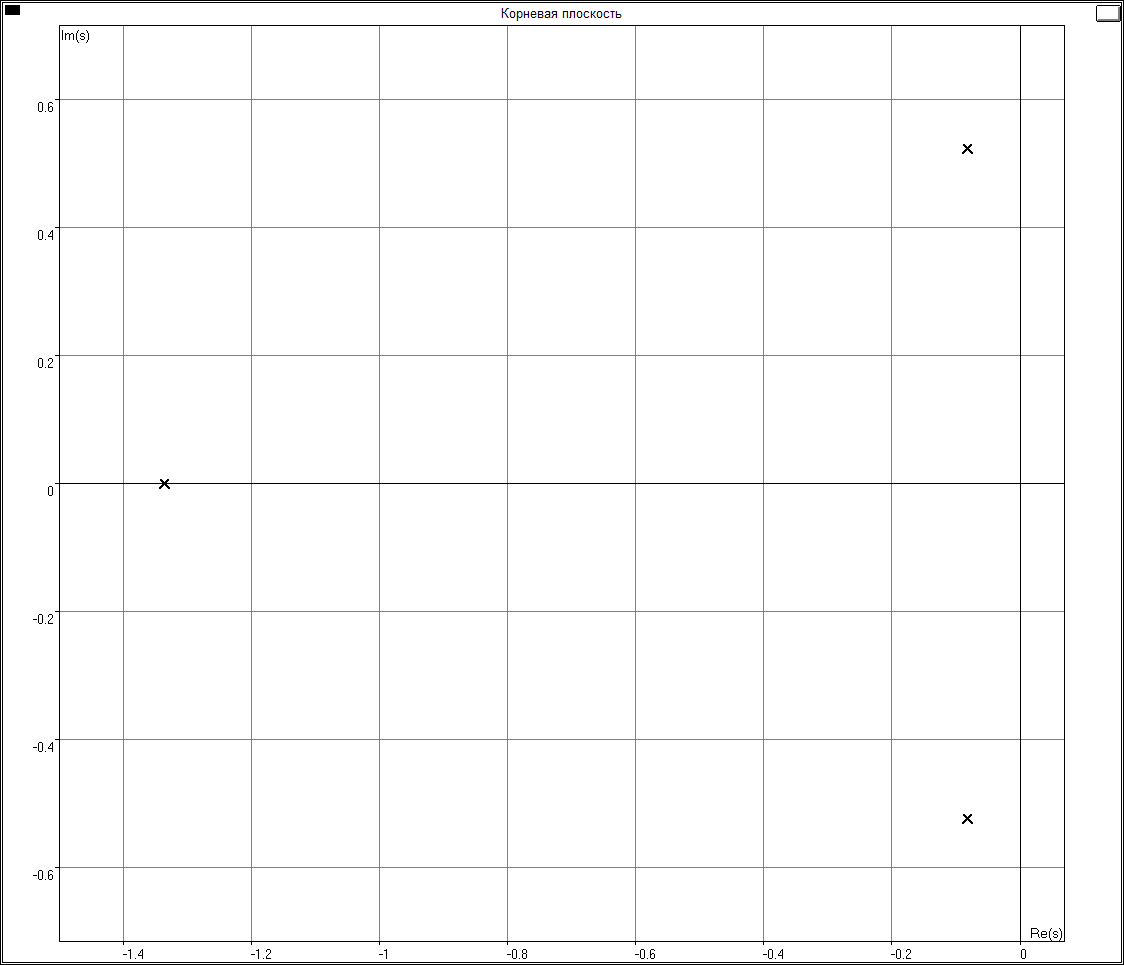 k=0.75
k=0.75
Временные характеристики:
 k=1.5
k=1.5
 k=1.2
k=1.2
 k=0.75
k=0.75
Частотные характеристики:
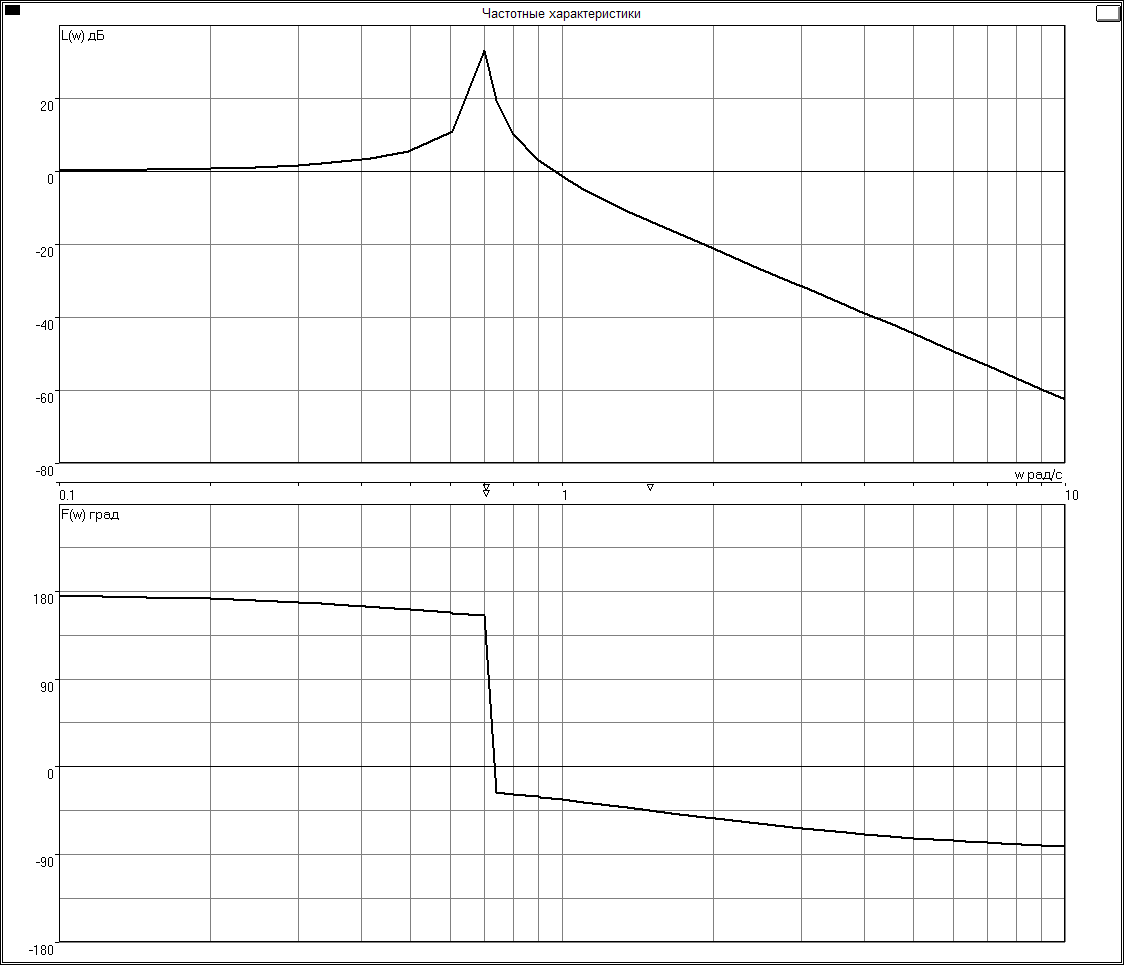
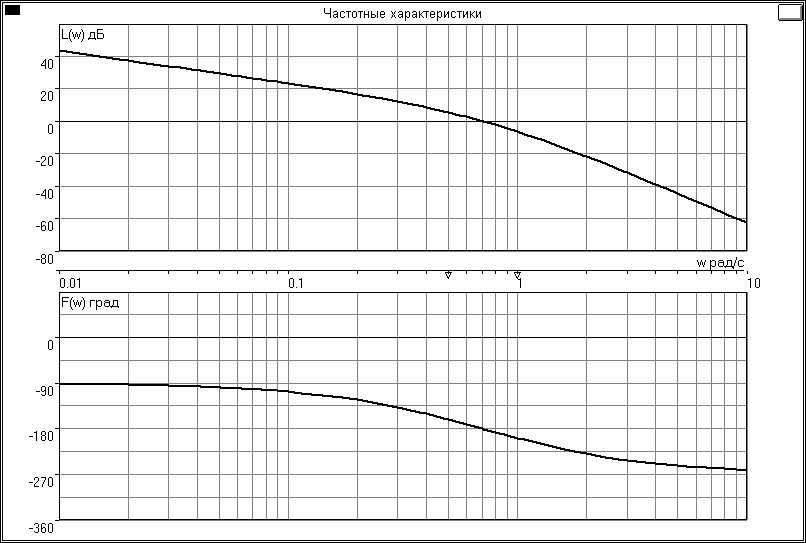 k=1.5
k=1.5

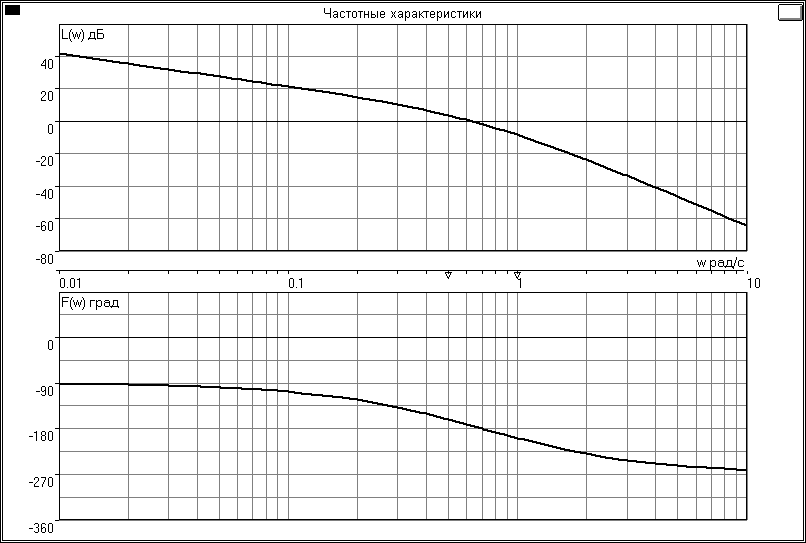 k=1.2
k=1.2

 k=0.75
k=0.75
Ответить на вопросы:
-
Какой вид имеют ЧХ системы в разомкнутом состоянии при k = kкр?

-
Чему равны запасы устойчивости замкнутой системы по амплитуде L и по фазе при k = 0.5kкр; k = 0.8kкр?
k = 0.5kкр=0.75
Запас по фазе: 20.0381 град
Запас по модулю: 6.0206 дБ
k = 0.8kкр=1.2
Запас по фазе: 6.1736 град
Запас по модулю: 1.9382 дБ
Задача 5.4. В системе из задачи 5.3 ввести в прямую цепь последовательно дополнительное звено с ПФ W(s) = s + 1. Для характеристического полинома замкнутой системы, имеющего вид:
![]()
построить корневой годограф при изменении k в диапазоне 0 k < , приняв = T1 = 1с.
 k=1
k=1
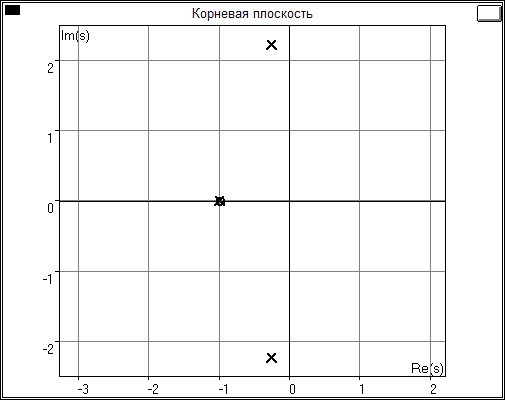 k=10
k=10
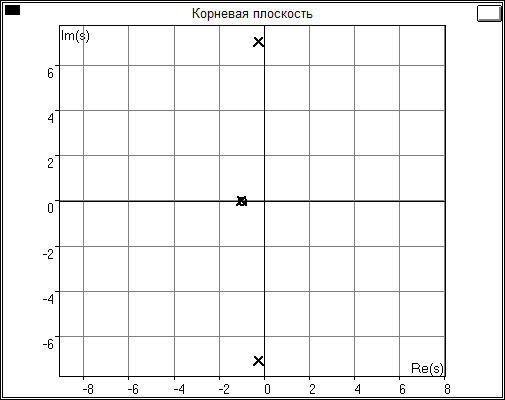 k=100
k=100
Ответить на вопросы:
-
Чем объясняется неподвижность одного из корней ХП?
![]() ,
т.е. корень s
= -1 не зависит от k.
,
т.е. корень s
= -1 не зависит от k.
-
Как объяснить характер траекторий подвижных корней ХП D(s) при изменении k?
При увеличении коэффициента усиления k корни ХП расходятся относительно вещественной оси и при некотором значении k переходят в правую полуплоскость. Это объясняется тем, что чем больше КУ k, тем больше амплитуда колебаний системы и при критическом значении k система становится неустойчивой.
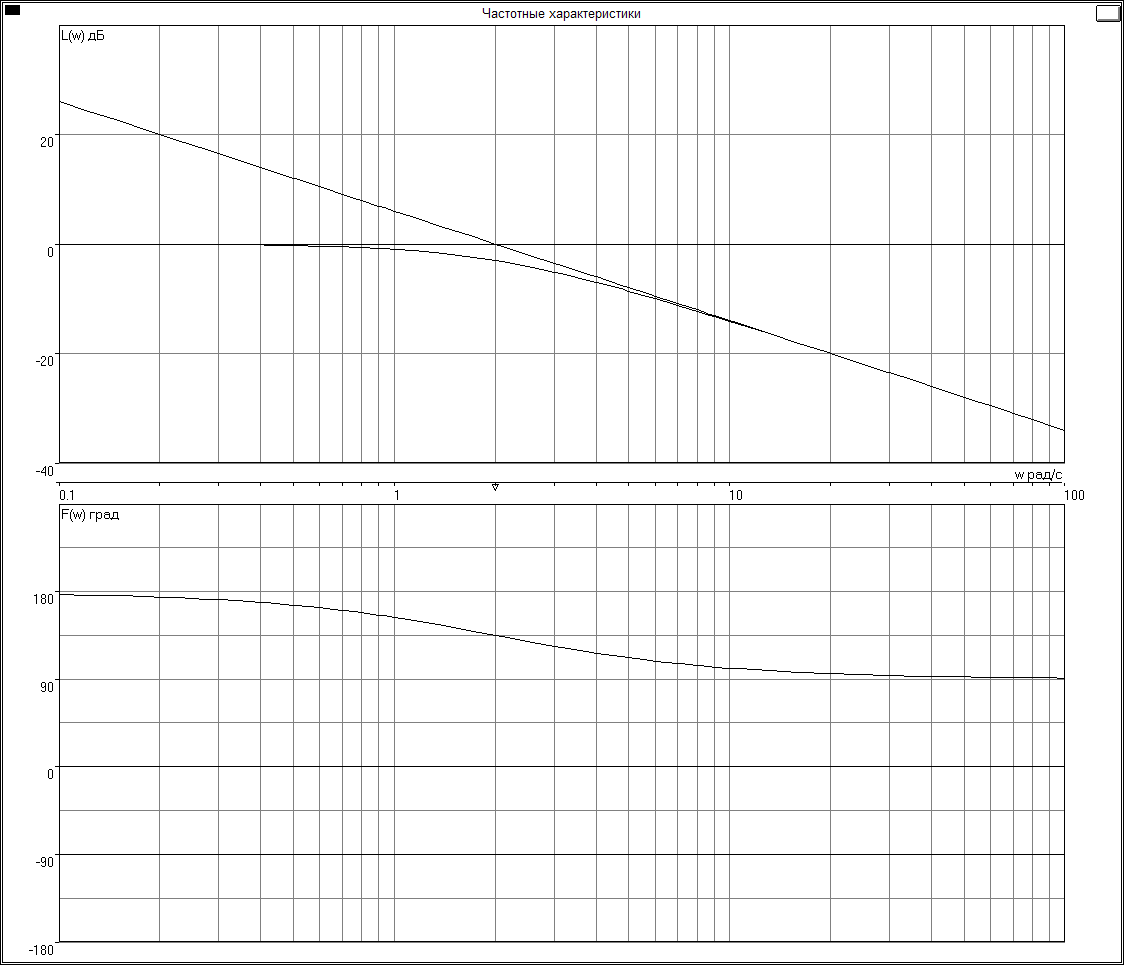
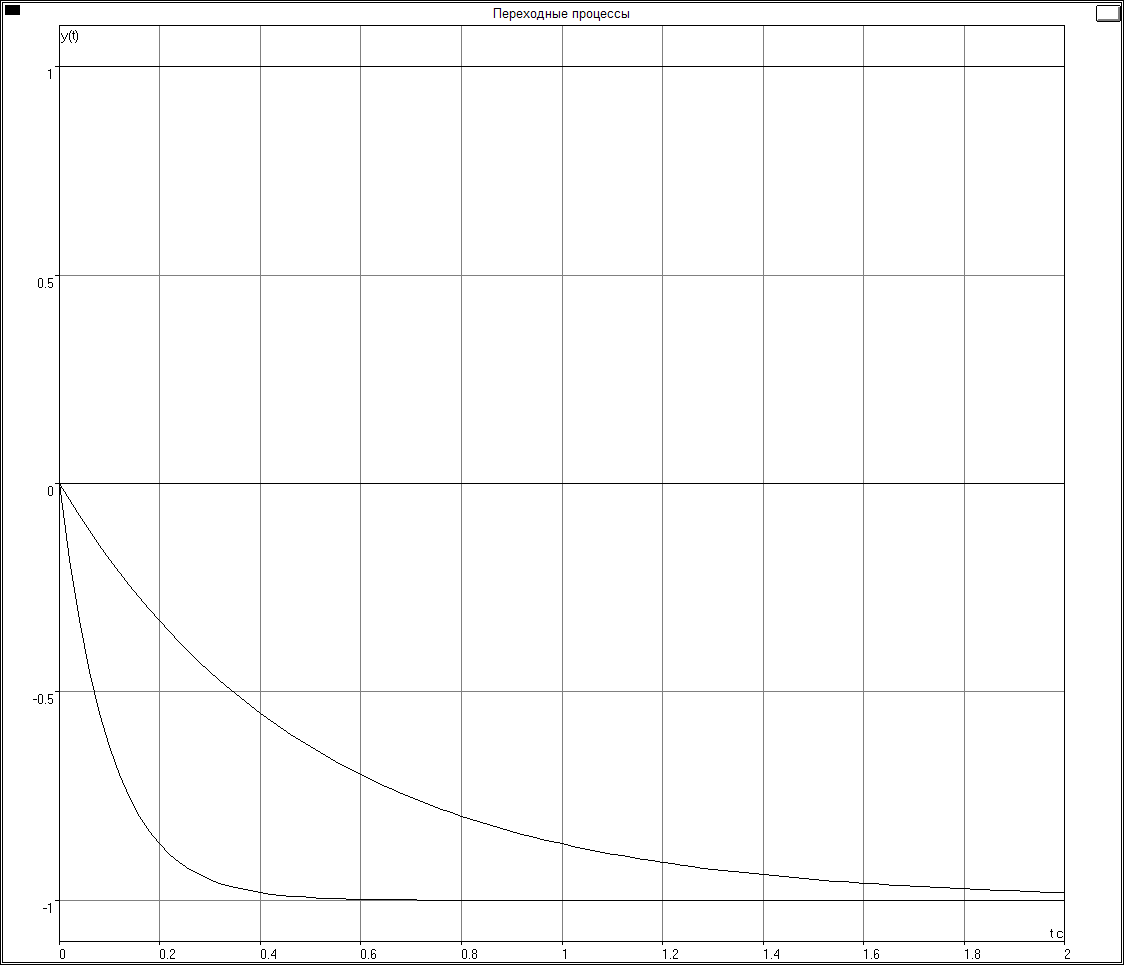
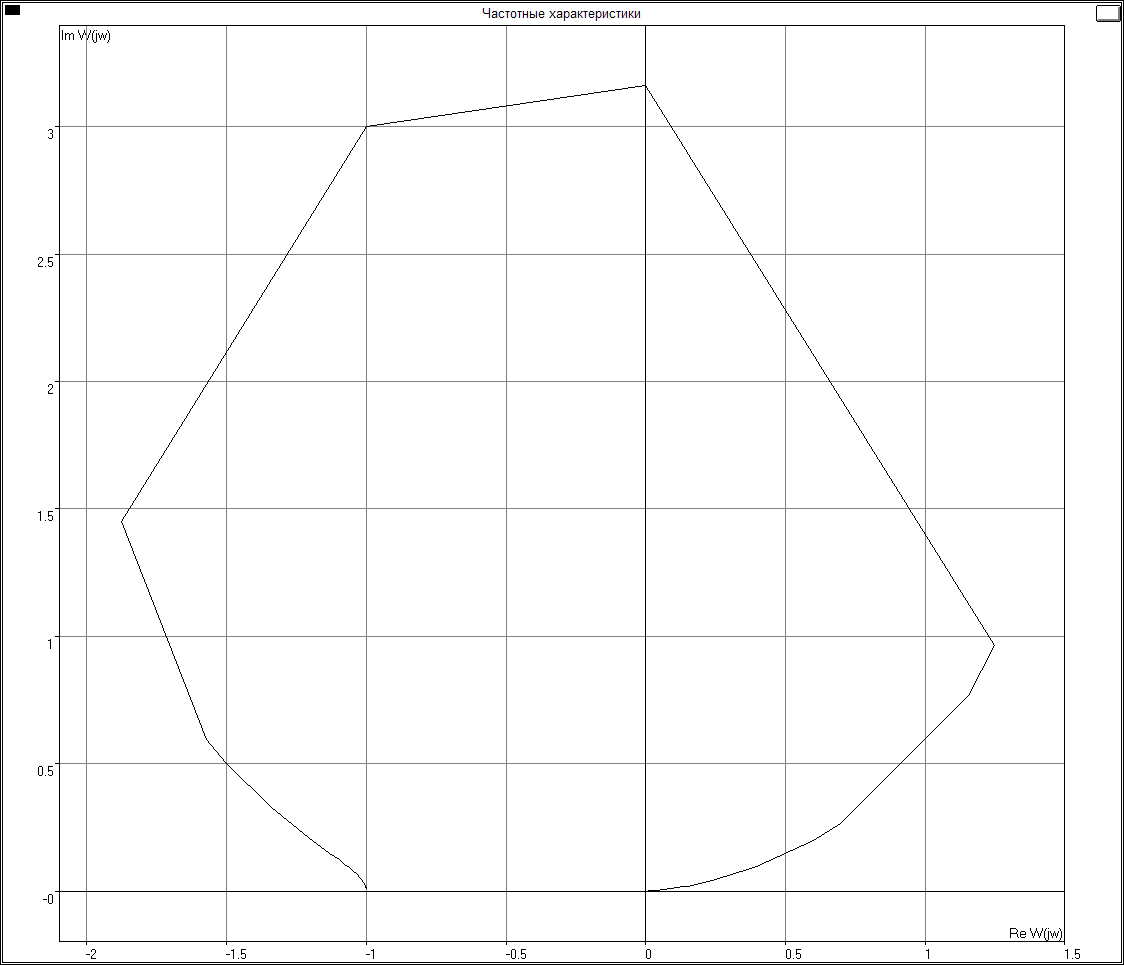
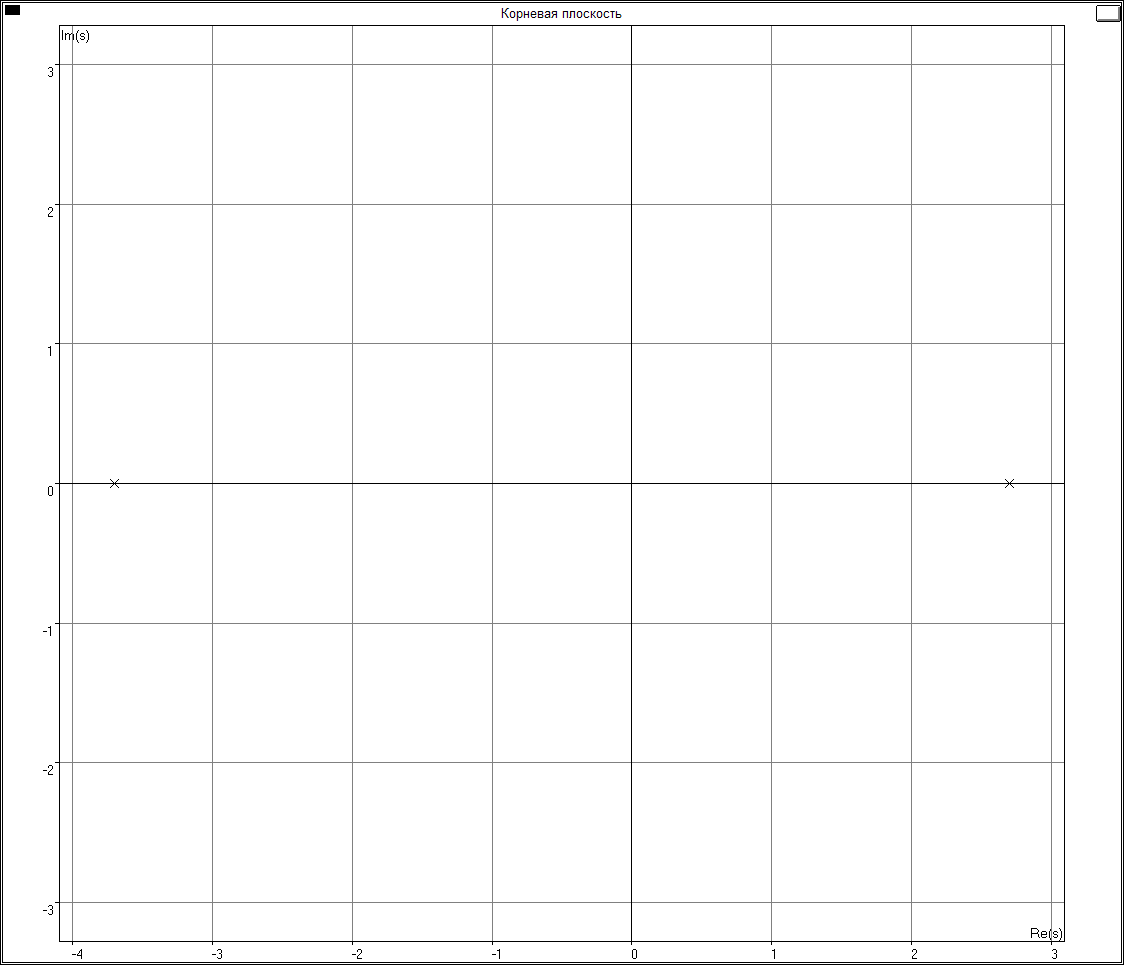
Задача 5.5. Принять ПФ W(s) в виде:
![]()
Используя изложенную выше методику оценки подвижности корней, использующую ЛАЧХ разомкнутой системы L0(), определить области частот 1 (усиление контура велико), 2 (усиление контура мало) и приближенные значения отдельных корней ХП замкнутой системы, которые принадлежат этим областям. Найти точные значения корней ХП и оценить эффективность методики для рассматриваемого примера.
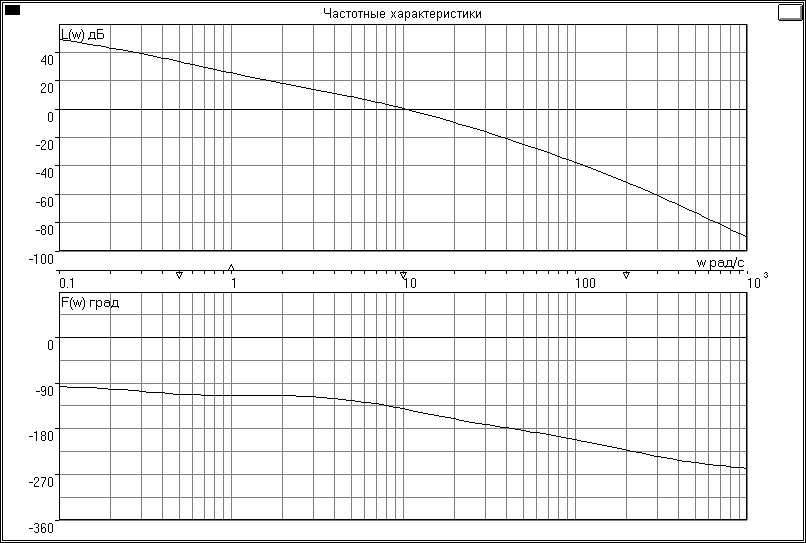
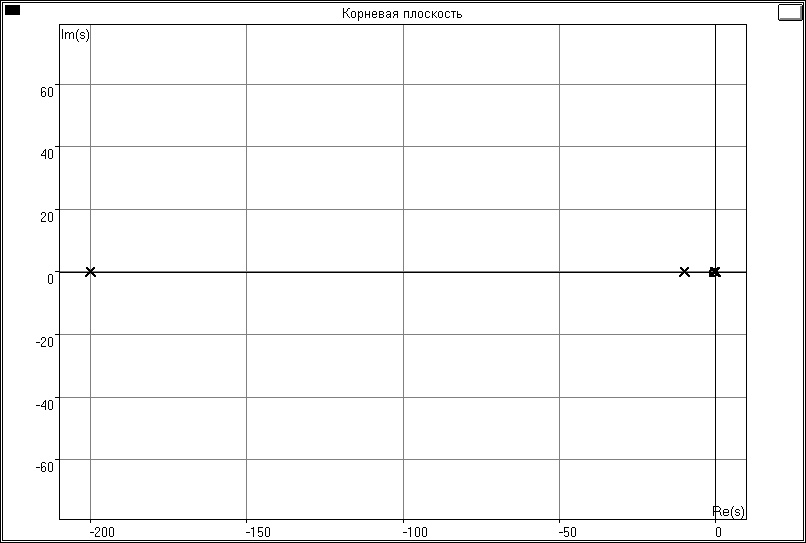
Значения корней:
Ноль:
-1.000000
Полюса:
0.000000
-1.000000
-10.000000
-200.000000
Значит при w = 1 c-1 наклон ЛАЧХ меняется на +20 дБ/дек
при w = ½ c-1 w = 10 c-1 w = 200 c-1наклон ЛАЧХ меняется на -20дБ/дек
