Тема 2. Повторные независимые испытания

2.1. Формула Бернулли

Применяется для нахождения вероятности появления события А в n повторных независимых испытаниях равно K раз.

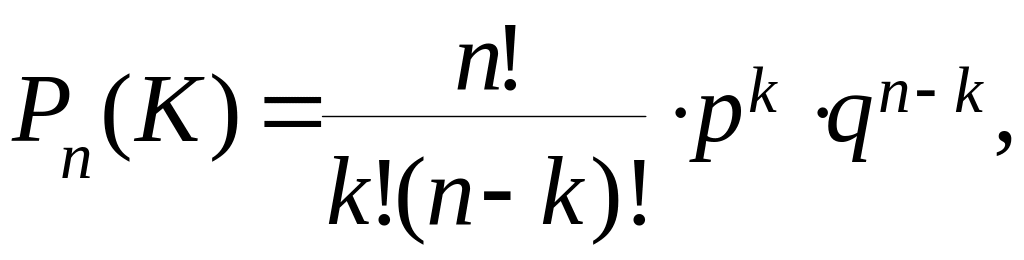
где n – число испытаний; K – число появлений события А, 0  K  n; p – вероятность появления события А в одном испытании; q = 1 – p.

Вероятность того, что событие А наступит:

а) Р_n(менее К раз) = Р_n(0) + Р_n(1) + … + Р_n(К–1);

б) Р_n(более К раз) = Р_n(К+1) + Р_n(К+2) + … + Р_n(n);

в) Р_n(не менее К раз) = Р_n(К) + Р_n(К+1) + … + Р_n(n);

г) Р_n( не более К раз) = Р_n(0) + Р_n(1) + … + Р_n(К);

д) Р_n(от К₁ до К₂ раз) = Р_n(К₁) + Р_n(К₁+1) + … + Р_n(К₂);

е) Р_n(хотя бы один раз) = 1 – Р_n(ни одного раза) = 1 – Р_n(0).

Пример. Товаровед проверяет на стандартность однотипные изде­лия, поступившие от поставщика, среди которых 10% бракованных. Ка­кова вероятность того, что из шести проверенных изделий окажется: а) два бракованных; б) хотя бы одно бракованное; в) не менее поло­вины бракованных?

Решение. По условию n = 6, Р = 0,1, q = 0,9. Воспользуемся формулой Бернулли: а)

б) Р₆(хотя бы одно бракованное изделие) = 1 – Р₆(0) =

в) Р₆(не менее трех бракованных) = Р₆(3) + Р₆(4) + Р₆(5) + Р₆(6) =

2.1. Локальная теорема Лапласа

Применяется для приближенного нахождения вероятности появле­ния события А «К» раз в n независимых испытаниях. Используется вместо формулы Бернулли, применение которой неудобно при больших n (n  10).

,

(х) – функция, свойства которой описаны в пункте 2.3. Значения (х) бе­рутся по таблице (приложение 1).

Пример. Найти вероятность того, что событие А наступило ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0,25.

Решение. По условию n = 243, k = 70, р = 0,25, q = 0,75. Так как n=243 достаточно большое число, воспользуемся формулой Лапласа:

По таблице (приложение 3) найдем (1,37) = 0,1561. Искомая вероятность:

Функция (х).

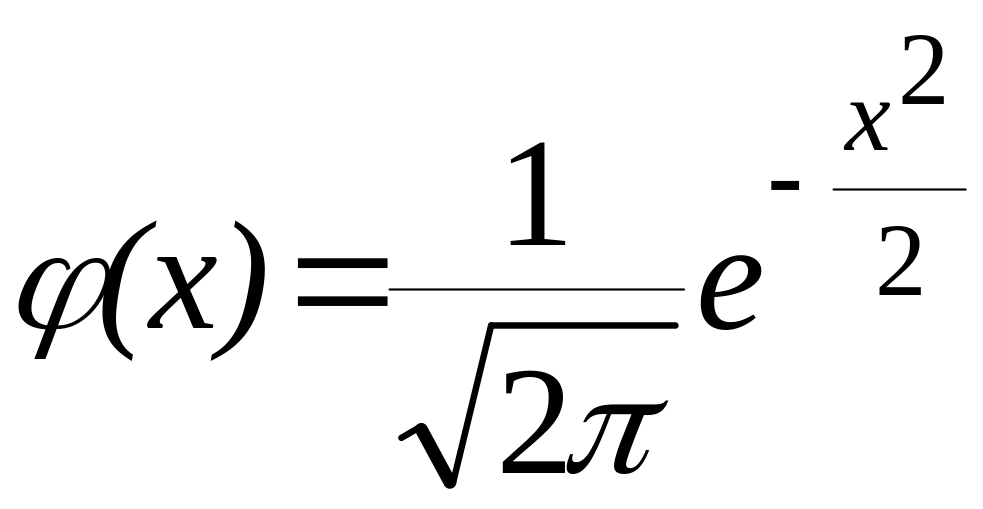
Свойства функции:

1) область определения: х (-; +);

2) множество значении: (х) > 0;

3) четность: (–х) = (х);

4) максимум при x = 0,

5) возрастание при х (-; 0), убывание при х (0; +);

6) перегибы в точках х =  1,

7) при х   , (х)  0.

0.3989

0.242

-1 0 1 x

Геометрически это означает, что площадь под кривой Гаусса равна 1.

Значения функции (х) берутся по таблице (приложение 1). В таблице помещены значения х [0; 4]. Если х  4, то (х) = 0. Для отрицательных значений (–х) = (х).

2.4. Интегральная формула Лапласа

Применяется для приближенного нахождения вероятности появления события А при n повторных испытаниях от К₁ до К₂ раз.

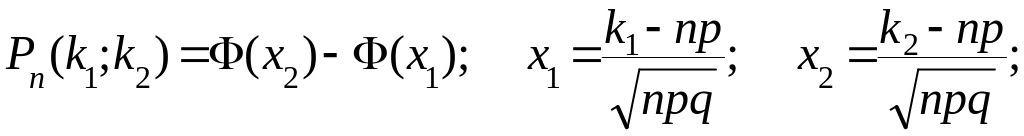
Ф(х) – функция Лапласа (см. 2.5). Значения Ф(х) берутся по таблице (приложение 2).

Пример. Вероятность появления события в каждом из 100 независимых испытаний постоянна и равна Р = 0,8. Найти вероятность того, что событие появится: а) не менее 75 раз и не более 90 раз; б) не менее 75 раз; в) не более 74 раз.

Решение: воспользуемся интегральной формулой.

а) по условию n = 100; р = 0,8; q = 0,2; К₁ = 75; К₂ = 90.

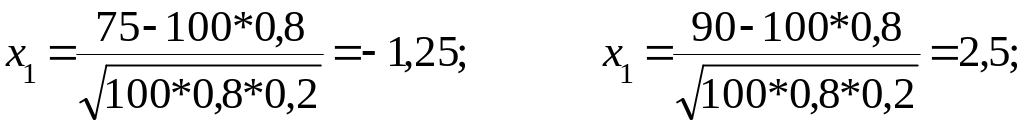
P₁₀₀(75; 90) = Ф(2,5) – Ф(–1,25) = Ф(2,5) + Ф(1,25) = 0,3944 + 0,4938=0,8882.

По таблице (приложение 2) Ф(2,5) = 0,4938, Ф(1,25) = 0,3944.

Искомая вероятность Р₁₀₀(75;90) = 0,8882.

б) не менее 75 раз означает появление события 75 раз, либо 76, либо 77, ... , либо 100. Таким oбpазом, K₁ = 75, К₂ = 100, тогда

P₁₀₀(75; 100) = Ф(5) – Ф(–1,25) = 0,5 + 0,3944 = 0,8944.

в) события – «А появилось не менее 75 раз» и «А появилось не более 74 раз» противоположны, поэтому сумма их вероятностей равна 1. Следовательно, P₁₀₀(0; 74) = 1 – P₁₀₀(75; 100) = 1 – 0,8944 = 0,1056.