Многоцелевые задачи (мцз)
Задачи у которых существует несколько критериев оптимальности принято называть многоцелевыми.
F
L(x)=
(i=1….m)
Величины Bi, Alj, Сj, являются известными постоянными
L – конечна
Кроме того предполагается что в области допустимых решений не существует решений одновременно удовлетворяющим всем критериям оптимальности.
Улучшение какого-либо одного решения может происходить только за счет ухудшения другого решения.
Это приводит к поиску компромисса между целевыми функциями задач.
При решении многоцелевых задач используются два основных метода
Метод уступок – все критерии максимизируются; каждому критерию ставим в соответствие некое число 0<ks<1 (S=1….L). число Ks характеризует максимальное отклонение S-го критерия от своего экстримального значения, полученного при отсутствии всех остальных критериев. При решении задачи все критерии должны быть проранжированы по уровню значимости т.е наиболее значимый критерий первый, следующий на втором и т.д.
Процедура решения задачи методом уступок
Решить задачу по наиболее значимому критерию без учета всех остальных
F*1(x) – найденное максимальное решение по первому критерию
Произвести уступку по первому критерию и в систему ограничений ввести новое ограничение f1(x) k1*f*1(x) и вводим его в систему ограничений.
Решить задачу по второму критерию при расширенной системе ограничений F*2(x)
Сделать уступку по второму критерию а в систему ограничений ввести новое f2(x) k2*f*2(x) и так далее для всех остальных решений (повторять шаги 3-4)
Значение переменных х1,х2….хn полученные при решении последней задачи будут являться суб-оптимальными для всех критериев.
ПРИМЕР
F(x)=X1+X2max
F
2(x)=X1+3X2min
3X1+2X2>=9
2X1-3X2=<8
-X1+X2=<2
X2=<5
Отклонение от максимального значения для первого критерии не более 40% (K1 = 0,6)
ШАГ 1 – решаем по первому критерию
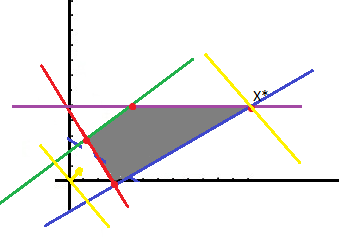
X2=5
2X1-15=6
X1=11,5
X*=(5;11,5)
F*1(X)=16,5
ШАГ 2 – производит уступку
X1+X2>=0,6*16
X1+X2>=9,9
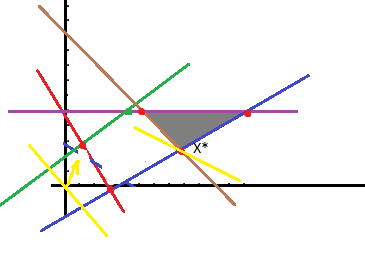
X1+X2=9,9
2X1-3X2=8
5X2=11,8
X2=2,36
X1=7,54
Это решение является компромиссным.
Метод равных и наименьших отклонений (РиНО) – относительные отклонения от своих экстремальных значений являются равными и минимально возможными
F*1, F*2…F*L.
Экстремальные значения соответствующих критериев оптимальности полученные при решении соответствующих задач без учета всех остальных критериев
Рассмотрим относительное отклонение соответствующих критериев от своих экстремальных значений
|F1-F*1|/|F*1|=|F2-F*2|/|F*2|=|FL-F*L|/|F*L|
|
F1-F*1|/|F*1|=|F2-F*2|/|F*2|
||F1|/|F*1|-1|=||F2|/|F*2|-1|
Оба критерия максимизируются
1-F1/F*1=1-F2/F*2 - раскрыли модуль
Q1=1-F*1
Q2=1-F*2
Q1f1-q2f2=0
Оба критерия минимизируются.
F1/F*1-1=F2/F*2-1
Таким образом если оба сравниваемых критерия максимизируются/минимизируются при решении многоцелевой задачи методом РиНО в исходную систему ограничений необходимо ввести ограничения вида q1f1-qLfL=0
1-(F1/F*1)=(F2/F*2)-1
F1/F*1+F2/F*2=1
q1f1+q2f2=2
Если сравниваемые критерии один максимизируется и один минимизируются то в исходную систему необходимо ввести дополнительное ограничение вида
q1f1+qLfL=2
требование минимальности отклонений приводит к тому чтобы в исходную систему ограничений должны быть введены дополнительные ограничения следующего вида
Величины Fl рассматриваются как новые дополнительные переменные задачи.
При решении МЦЗ методом РиНО в исходную систему ограничений должно быть введено дополнительно 2L-1 ограничений где L – количество критериев.
ПРИМЕР
Требуется решить МЦЗ следующего типа
F(x)=1X1+2X2max
F
2(x)=X1+X2min
X1+2X2=<6
X1=<4
X2=<5
X2=<5
F*1=14
F*2=3
q1=1/14
q2=1/3
q1f1+q2f2=2
1/14(X1+2X2)+1/3(X1+X2)=2
X1+2X2-f1=0
X1+X2-f2=0
При решении задачи по расширенной системе ограничений в качестве критерия оптимальности может быть выбрал любой критерий.