22. Вероятность попадания значений непрерывной случайной величины в заданный интервал для нормального распределения плотности вероятностей.
Для
нормально распределенной случайной
величины соответственно получим:
.
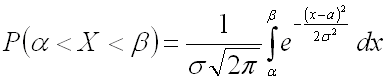где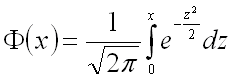 
–
функция Лапласа.
Вывод:
вероятность того, что нормально
распределенная случайная величина
примет
значение, принадлежащее интервалу
,
равна:
,
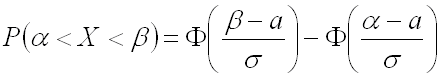где 
–
математическое ожидание, 
–
среднее квадратическое отклонение
данной случайной величины.
23. Расчет вероятности заданного отклонения нормальной случайной величины. Правило трех сигм.
Вычислим
вероятность того, что отклонение
нормально распределенной случайной
величины
от
своего математического ожидания по
абсолютной величине не превысит 
,
то есть вероятность осуществления
неравенства 
.
Заменим
неравенство с модулем равносильным
ему двойным неравенством:
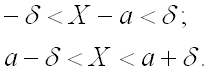Теперь
мы можем воспользоваться формулой для
нахождения вероятности попадания в
заданный интервал нормальной случайной
величины, где границами интервала
являются
:
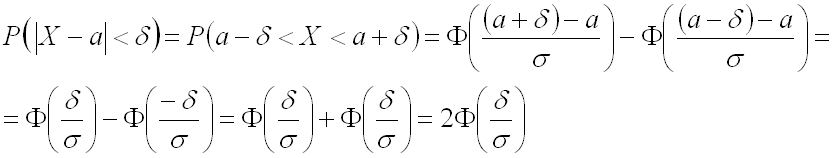(в
последних преобразованиях использовано
свойство нечетности функции
Лапласа: 
).
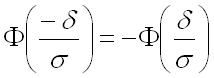Вывод:
вероятность того, что отклонение
нормально распределенной случайной
величины
от
своего математического ожидания по
абсолютной величине не превысит
,
равна:
,
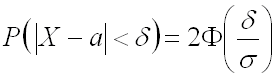где
–
математическое ожидание,
–
среднее квадратическое отклонение.
Правило трех сигм
Вычислим
вероятность того, что отклонение
нормально распределенной случайной
величины
от
своего математического ожидания по
абсолютной величине не превысит 
.
Воспользуемся
формулой для нахождения вероятности
заданного отклонения, в которую в
качестве
подставим
:
.
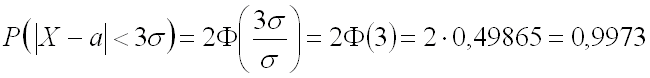Таким
образом, вероятность того, что отклонение
случайной величины
по
абсолютной величине будет меньше
утроенного среднего квадратического
отклонения, равна 0,9973.
Другими
словами, вероятность того, что абсолютная
величина отклонения превысит
,
составляет всего 0,0027. Такое событие,
исходя их принципа невозможности
маловероятных событий, можно считать
практически невозможным.
Вывод
(правило трех сигм): если
случайная величина распределена
нормально, то абсолютная величина ее
отклонения от математического ожидания
не превосходит утроенного среднего
квадратического отклонения.
24. Показательное распределение плотности вероятностей непрерывной случайной величины и вероятность попадания в заданный интервал для данного распределения. 25. Числовые характеристики показательного распределения: математическое ожидание, дисперсия, среднее квадратичное отклонение. Функция надежности.
Экспоненциальное или показательное распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.
Непрерывная случайная величина имеет показательное распределение с параметром > 0, если она принимает только неотрицательные значения, а ее плотность распределения p (x )и функция распределения F (x) имеют соответственно вид:
,
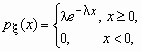
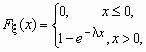
Видно, что в случае показательного распределения математическое ожидание и среднее квадратическое отклонение равны.
Плотность
распределения при различных значениях 
.
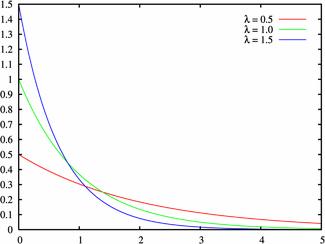
В отличие от нормального распределения, показательный закон определяется только одним параметром λ. В этом его преимущество, так как обычно параметры распределения заранее не известны и их приходится оценивать приближенно. Понятно, что оценить один параметр проще, чем несколько.
Теперь можно найти вероятность попадания показательно распределенной случайной величины в интервал (а, b):
.
Значения функции е-х можно найти из таблиц.
Функция надежности.
Показательное распределение широко используется в теории надежности.
Допустим, некоторое устройство начинает работать в момент времени t0=0, а через какое— то время t происходит отказ устройства.
Обозначим Т непрерывную случайную величину — длительность безотказной работы устройства.
Таким образом, функция распределения F(t) = P(T<t) определяет вероятность отказа за время длительностью t.
Вероятность противоположного события (безотказная работа в течение времени t) равна R(t) = P(T>t) = 1 — F(t).
Определение. Функцией надежности R(t) называют функцию, определяющую вероятность безотказной работы устройства в течение времени t.
R(t) = p(T > t) = 1 – F(t).
Показательный закон надежности.
Часто длительность безотказной работы элемента имеет показательное распределение, то есть
F(t) = 1 – e-λt .
Следовательно, функция надежности в этом случае имеет вид:
R(t) = 1 – F(t) = 1 – (1 – e-λt) = e-λt .
Определение 6.4. Показательным законом надежности называют функцию надежности, определяемую равенством
R(t) = e-λt ,
где λ – интенсивность отказов.
**
Часто на практике длительность безотказной работы подчиняется показательному закону распределению.
Вообще говоря, если рассматривать новое устройство, то вероятность отказа в начале его функционирования будет больше, затем количество отказов снизится и будет некоторое время иметь практически одно и то же значение. Затем (когда устройство выработает свой ресурс) количество отказов будет возрастать.
Другими словами, можно сказать, что функционирование устройства на протяжении всего существования (в смысле количества отказов) можно описать комбинацией двух показательных законов (в начале и конце функционирования) и равномерного закона распределения.
Важным свойством, позволяющим значительно упростить решение задач теории надежности, является то, что вероятность безотказной работы устройства на интервале времени t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности времени t.
Таким образом, безотказная работа устройства зависит только от интенсивности отказов l и не зависит от безотказной работы устройства в прошлом.
Так как подобным свойством обладает только показательный закон распределения, то этот факт позволяет определить, является ли закон распределения случайной величины показательным или нет.