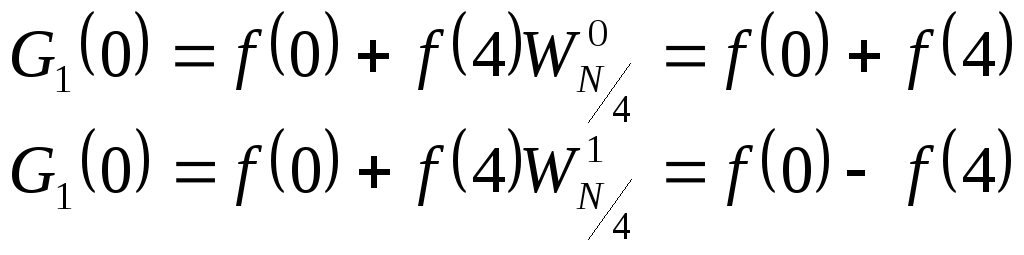8.4.2 Метод поочередного удвоения

Как обсуждалось в предыдущем разделе, двумерное преобразование Фурье может быть разбито на два вычислительных шага, каждый из которых является одномерным преобразованием Фурье, а обратное преобразование Фурье может быть выполнено как прямое над сопряженной функцией и также разбито на два одномерных. Т.о. алгоритм одномерного преобразования Фурье будет ядром всей операции и именно он требует особого внимания к обеспечению вычислительной эффективности.

Дискретное преобразование Фурье можно переписать в соответствии с 8.2:

(8.72)

Произведем перегруппировку тем же способом, что и для 8.60 и 8.61 константный множитель и обозначим его , т.ч. дискретное ПФ преобразуется в

(8.73)

что дает систему N уравнений, гдеN соответствует числу различныхu. Легко видеть из 8.73, что для вычисления каждого уравнения необходимоN умножений иN сложений или всего2N² комплексных арифметических операций для всего массива (илиN² если f(x) - вещественная функция). КогдаN становится велико, число вычислений, необходимых для преобразования Фурье становится ужасно. Однако, вычисление может быть упрощено чтобы сделать технику преобразования практичной. Это стало возможным только когда было предложено быстрое преобразование Фурье (БПФ - 1965). Фундаментальный принцип БПФ заключается в декомпозиции ДПФ на последовательность из N преобразований значительно меньшей сложности.

Положим, что , гдеL - положительное целое число, тогда выражение 8.73 может быть разбито на две части:

(8.74)

где . СуществуетN слагаемых (или последовательностьN слагаемых) для каждого уравнения из описанной выше системы. Выражение 8.74 может, таким образом, быть задано в следующей форме с целым положительнымr:

(8.75)

или

(8.76)

Первая сумма справа содержит последовательность из N/2слагаемых. Заметим, что по определению

(8.77)

Используем как ядро последовательности изN/2слагаемых, тогда имеем

(8.78)

или

(8.79)

где

Рисунок 8.41 Реализация уравнения 8.78 для

Заметим, что

И G(u) иH(u) - периодические с периодомN/2. Осторожный анализ уравнения 8.78 при помощи 8.80 показывает некоторые интересные свойства этих выражений. Отметим, что в 8.78 и 8.79N-точечное дискретное вычисление может быть разделено на две части. Каждая часть связана с вычислениемN/2-точечных преобразований. Разумеется, время вычисленияN/2-точечного преобразования существенно меньше, чемN-точечного ДПФ.

В продолжение этого анализа N/2-точечное преобразование может быть разделено на дваN/4-точечных и так далее для любогоNявляющегося степенью 2. Реализация этого выражения составляет суть метода последовательного удвоения.

Реализация уравнения 8.78 показана на рисунке 8.41 для N= 8. ВерхниеN/2 точек - этоf(x)'ы для четных значений аргумента, а нижние - для нечетных. Подстановка значений 0, 1, 2 и 3 дляuв

(8.81) (8.82)

дает , которые комбинируются в соответствии с графом переходов, показанным на рисунке для получения преобразований Фурье.на графе показывают множители перед, необходимые для 8.79. Заметим, что- периодические с периодом, который равен 4 в данном случае (т.е.и т.д.). Поэтому. При помощи этого алгоритма сокращается число операций, необходимых для восьмиточечного преобразования Фурье. Общее число комплексных операций уменьшается при помощи этого алгоритмаc до необходимых для алгоритма удвоения. Здесь второе слагаемое это число математических операций, необходимых для каждогоN/2-точечного ДПФ, а первое - число необходимых операций сложения. Заменяянаи обозначаяв уравнении 8.78 мы разбиваемG(u)на две части, одна для четныхr, другая - для нечетных.

(8.83)

где

(8.84)

представляет часть для четных r, а

(8.85)

для нечетных. Обе функции периодические с периодом . Аналогично мы имеем

где представляет частьдля четных аргументов, а- для нечетныхr. И вновь обе функции периодические с периодомN/4.

Рис. 8.42 Реализация уравнения 8.83 для N=8

N/2-точечное преобразование Фурье можно разбить как показано на рисунке 8.42. ВерхнийN/4-ДПФ блок реализует 8.84, а нижний - уравнение 8.85.

Декомпозиция ДФТ обеспечивает переход от - точечного преобразования к двухточечному. В нашем случае, когдаN=8,N/4-точечное преобразование это двухточечное, где

(8.87)

Полное восьмиточечное ДПФ (или БПФ при N=8) реализуется как показано на рисунке 8.43.

Таким образом, посредством алгоритма последовательного удвоения общее число комплексных операций уменьшается с исходного до, а затем дои так далее в зависимости от числа стадий декомпозицииN-точечного преобразования. Если N велико и равно, то число стадий равноL, а число комплексных операций изменяется сдо. Для приведенного примера число комплексных операций равно.

Для хранения структуры алгоритма входы блока ДПФ должны быть расположены в порядке, необходимом для последовательной процедуры из уравнения 8.78. Для вычисления ДПФ для восьмиточечной функции входы четных аргументовиспользуются для верхнего-точечного ДПФ (четырехточечного в данном случае), а нечетные аргументыиспользуются для нижнего четырехточечного преобразования.

Рисунок 8.43 Полное восьмиточечное БПФ

Каждое четырехточечное преобразование вычисляется через двухточечные. Мы должны разделить первый набор входов на четную и нечетную части, т.е. расположить входы в порядке для выполнения алгоритма последовательного удвоения, показанного на рисунке 8.44. Нетруднозаметить, что входы и выходы располагаются в "бит-реверсивной" последовательности, как показано в таблице 8.1. Отметим, что на рисунке 8.43, где. Мы также имеем. Используя эту зависимость получаем рисунок 8.45. Аналогичные аргументы справедливы при. Число шагов равно, а число комплексных операций равно. Переупорядочение битов для алгоритма последовательного удвоения и его реализации показано соответственно на рисунках 8.46 и 8.47. Как уже отмечалось ранее, техника преобразования Фурье стала широко использоваться только после того, как в 1969 году Кули и другими была предложена реализация алгоритма БПФ на Фортране.

Рис. 8.44 Перестановка входов для алгоритма последовательного удвоения

Эта программа состоит из четырех частей, первая из которых служит для спецификации параметров (строки 1-6). Вторая часть (т.е. строки с 7 до 18), включая цикл "DO 3" предназначена для обработки данных в бит-реверсивной последовательности для последующего вычисления методом последовательного удвоения. Третья часть программы (строки 19-30), включая цикл "DO 5" производит необходимые действия по реализации последовательного удвоения. В последней части, включающей цикл "DO 6"результаты делятся наN. Читатели могут проанализировать эту программу приN=16и увидеть детально шаги по перестановке данных:

или

Таблица 1 Пример бит-реверсивной перестановки входов в БПФ

Входной порядок	Аргумент	Двоичное кодирование			Бит-реверсивное кодирование			Новый аргумент	Выходной порядок
	0	0	0	0	0	0	0	0
	4	1	0	0	0	0	1	1
	2	0	1	0	0	1	0	2
	6	1	1	0	0	1	1	3

Рис. 8.45 Бит-реверсивная связь между входами и выходами в БПФ

Рис. 8.46 Перестановка входов при методе последовательного удвоения для N=16

Рис. 8.47 Бит-реверсивная связь между входами и выходами БПФ при N=16

Эти перестановки символически показаны на рис. 8.49.

Для N=16 "большой циклDO 5" повторяется 4 раза. Это связано сстадиями. В течение первой стадии каждая "бабочка" преобразования выполняется для пар

Рисунок 8.48 Реализация алгоритма последовательного удвоения на Фортране (адаптировано из Кули и др. 1969 г.)

Рисунок 8.49 Входные данные после бит-реверсивной обработки при N=16

Произведенное нами ранее обсуждение прямого и обратного быстрых преобразований Фурье дало необходимую информацию для их реализации. Напомним, что прямое преобразование применимо для выполнения обратного путем использования операции комплексного сопряжения над его входными данными. Реализация алгоритма последовательного удвоения на Фортране приведена на рисунке 8.50, путем улучшения алгоритма одномерного преобразования, предложенного Кули и другими.

Отметим следующий факт: поскольку , число комплексных множителей, необходимых для реализации алгоритма последовательного удвоения уменьшается в 2 раза. Таким образом, общее число комплексных операций, необходимых для одномерного дискретного преобразования Фурье равно. Для двумерной функции изображениянам необходимоопераций дляu. По тем же соображениям нам необходимоопераций дляN значенийv. Общее число комплексных операций будет. Но если двумерное преобразование выполняется непосредственно, то необходимокомплексных операций. Таблица 8.2 показывает сравнительную характеристикуи.

До сих пор обсуждение концентрировалось на прямом преобразовании Фурье. Как уже говорилось, обратное преобразование выполняется сходным образом с заменой на.

Рисунок 8.50 Реализация БПФ для двумерного случая на Фортране