5.3. Метод Квайна-Мак-Класки

Основным недостатком метода Квайна является необходимость полного попарного сравнения ЭК на этапе нахождения первичных импликант. Поэтому при большом числе ЭК применение метода Квайна становится весьма затруднительным.

Мак-Класки предложил модернизацию алгоритма Квайна, которая заключается в том, что все ЭК, входящие в СДНФ записывается в виде двоичных чисел (номеров наборов), которые группируются по числу входящих в них единиц в непересекающиеся классы. В класс с номером i войдут все ЭК содержащие в своей двоичной записи i единиц. Попарное сравнение следует производить между соседними по номеру классами, так как только в них могут находиться склеивающиеся ЭК.

При образовании ЭК ранга меньше n вместо исключенных переменных ставится символ стирания x.

Этап 1. Нахождение первичных импликант.

Рассмотрим пример из раздела 5.2.

Исходная функция: f = (1, 3, 7, 8, 11, 12, 13, 18, 19, 24, 25, 26, 27).

Разбивая ЭК на классы по числу единиц, получим:

К₁=(00001*,01000*); К₂=(00011*,10010*,11000*,01100*); К₃=(00111*,01011*,01101*,10011*,11001*,11010*); К₄ = (11011*).

Образуем новые классы путем склеивания ЭК в соседних классах К₁...К₄:

К₁^*=(000x1,x1000,01x00*); К₂^*=(00x11,0x011*,x0011*,1001x*,1x010*,1100x*,110x0*,0110x); К₃^* = (x1011*,1x011*,110x1*,1101x*).

Строим ЭК 3-го ранга:

К₁^**=(000x1,x1000,01x00); К₂^** = (00x11,xx011,1x01x,110xx,0110x).

Таблица 5.3.

000x1

x1000

01x00

00x11

xx011

1x01x

110xx

0110x

Таблица 5.4.

x1000
01x00

Дальнейшие склеивания не возможны, поэтому переходим ко второму этапу (табл. 5.3.).

После вычеркивания избыточных столбцов и избыточных первичных импликант получим следующую таблицу (табл. 5.4.).

Полученная МДНФ примет вид:

000x1, 01x00, 00x11, xx011, 1x01x, 110xx, 0110x.

Нетрудно убедиться, что МДНФ, полученные двумя методами, совпадают.

5.4. Построение комбинационной схемы функции в заданном базисе

Под комбинационной схемой (КС) понимается логическая (цифровая) схема, выходные сигналы которой зависят только от значений входных сигналов в данный момент времени и не зависят от предшествующих входных и выходных сигналов. Можно сказать, что КС - это правильная схема, построенная из функциональных элементов, являющихся автоматами без памяти. В свою очередь, правильной называют логическую схему без обратных связей, соединения элементов в которой выполнены по правилам, соответствующим в функциональном отношении операции суперпозиции функций.

Основными задачами теории КС являются задачи анализа и синтеза схем.

Задача анализа состоит в нахождении общего конструктивного приема (алгоритма), позволяющего по любой КС построить функцию этой схемы и по ней определить зависимость сигнала на каждом из ее выходов от сигналов на входах. Решение этой задачи состоит в выписывании суперпозиций функций, определяемых соединением элементов схемы.

Задача синтеза КС сводится к представлению реализуемых функций в виде суперпозиции функций, реализуемых некоторым заранее заданным набором логических элементов.

Обобщенный алгоритм проектирования КС представлен на рис.5.5.

Данный алгоритм может видоизменяться в конкретных условиях проектирования. (Так составление таблиц истинности может не потребоваться для относительно простых БФ, которые легко записать в аналитической форме). Минимизация БФ может отсутствовать при использовании для реализации функции интегральных схем средней степени интеграции, таких как мультиплексоры, дешифраторы, программируемые логические матрицы (ПЛМ) и др.

Для получения функциональной схемы, соответствующей заданной функции алгебры логики, необходимо выразить эту функцию в некотором функционально полном базисе и сопоставить каждой элементарной функции функциональный элемент ей соответствующий. Процесс такого преобразования состоит в последовательной декомпозиции исходной формы представления заданной функции на подфункции, представленные в заданном функциональном базисе, и продолжается до тех пор, пока не будет найдена эквивалентная БФ в требуемом базисе.

Допустим, что у нас имеется некоторое исполнительное устройство – электрическая сирена и 4 датчика – два на окнах, один на двери и датчик снятия тревоги с пульта. Введем обозначения: х₁--сигнал датчика первого окна, х₂- сигнал датчика второго окна, х₃-сигнал датчика дверей, х₄-сигнал снятия тревоги с пульта. Сигнал включения электрической сирены представляет собой логическую функцию вида: у=f(х₁,х₂,х₃,х₄). Построив таблицу истинности для функции на основе словесного алгоритма работы схемы, получим запись функции:

y = _{1 2}x_{3 4} v ₁x_{2 3 4} v ₁x₂x_{3 4} v x_{1 2 3 4} v x_{1 2}x_{3 4} v x₁x_{2 3 4} v x₁x₂x_{3 4.}

Выполнив минимизацию логической функции, используя карту Карно, получим:

y = x_{1 4} v x_{3 4} v x_{2 4.}

Рассмотрим полученную функцию у в различных базисах.

В базисе 2И-НЕ получим:

y = = .

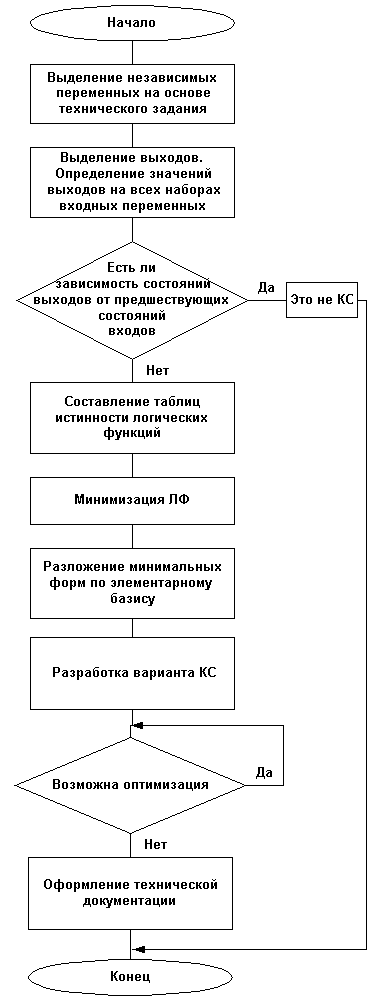
Рис. 5.5.

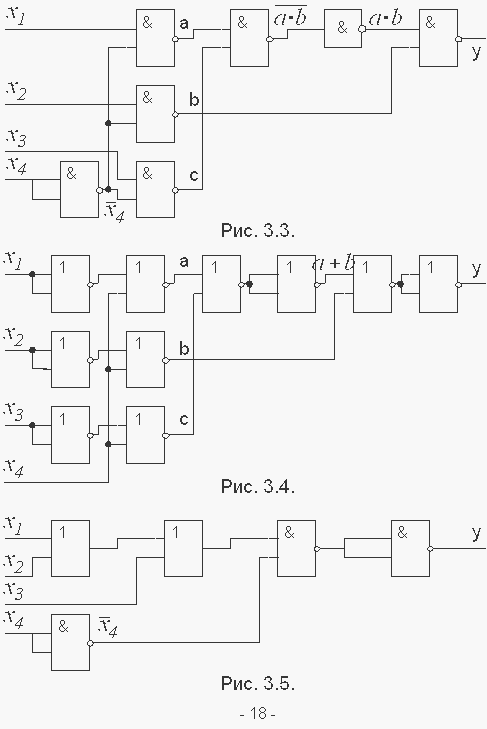
Рис. 5.6.

Обозначим a= , b= , c= .

Получится следующая физическая схема (рис. 5.6).

Построим схему в базисе 2ИЛИ-НЕ.

Обозначим a= , b= , c= .

a= , b= , c= .

Схема приведена на рис. 5.7.

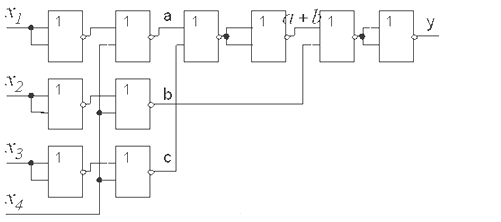
Рис. 5.7.