
- •Рабочая программа, методические указания и контрольные задания
- •1. Цель и задачи дисциплины
- •Распределение часов по формам обучения и видам занятий
- •2. Содержание лекционного курса
- •3. Практические занятия 17 часов
- •4. Контрольные задания
- •5. Методические указания к контрольным работам №1,2
- •5.1. Минимизация булевых функций с использованием карт Карно
- •5.3. Метод Квайна-Мак-Класки
- •6. Курсовой проект
- •7. Лабораторные работы
- •8. Вопросы к экзамену и зачету
3. Практические занятия 17 часов
1. Доказательство законов алгебры логики.
2. Решение задач алгебры высказываний.
3. Минимизация логических функций методом Карно.
4. Минимизация логических функций методом Квайна.
5. Минимизация логических функций методом Квайна-Мак-Класки.
6. Проектирование комбинационных схем.
7. Построение логических, матричных и граф-схем алгоритмов.
8. Разметка граф-схемы алгоритма по моделям Мура и Мили.
4. Контрольные задания
По дисциплине «Проектирование автоматизированных систем» студенты выполняют две контрольные работы. Первая контрольная работа состоит решении задачи минимизации булевых функций. Вторая работа заключается в построении логических схем функции в заданном базисе. Каждый студент выполняет свой вариант, который будет определяться последней цифрой шифра в зачетной книжке студента.
КОНТРОЛЬНАЯ РАБОТА №1,2
В первой контрольной работе необходимо для заданного варианта провести минимизацию булевой функции методами Карно, Квайна и Квайна-Мак-Класки. Варианты заданий представлены ниже:
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
Во второй контрольной работе необходимо построить логическую схему функции из первой работы в базисе:
1. 2И-НЕ
2. 2ИЛИ-НЕ
3. 2ИЛИ, 2И, НЕ
4. 2И-НЕ
5. 2ИЛИ-НЕ
6. 2ИЛИ, 2И, НЕ
7. 2И-НЕ
8. 2ИЛИ-НЕ
9. 2ИЛИ, 2И, НЕ
10. 2И-НЕ
5. Методические указания к контрольным работам №1,2
5.1. Минимизация булевых функций с использованием карт Карно
Метод минимизации булевых функций с использованием карт Карно является одним из самых наглядных и удобных с позиций инженерной практики.
Интервалом l-го ранга называется подмножество вершин двоичного n-мерного куба, соответствующее элементарной конъюнкции l-го ранга. Покрытием l-го ранга называется подмножество клеток карты Карно n-го порядка, соответствующее элементарной конъюнкции l-го ранга.
При задании булевой функции в виде ДНФ, задается множество ее единичных значений, что будет соответствовать комбинации интервалов на пространственном кубе или комбинации покрытий на карте Карно.
Рассмотрим функцию
трех переменных: f (x1,x2,x3)
=x1x2
v ![]() 1
3
v x1
2x3.
1
3
v x1
2x3.
ДНФ содержит три конъюнкции, которые представляются следующими интервалами (рис. 5.1.). На карте Карно получатся следующие покрытия (рис. 5.2.). Таким образом, существует взаимно однозначное соответствие между ДНФ, интервалами пространственного куба и покрытиями на карте Карно.
|
|
Рис. 5.2.
|
Задача нахождения МДНФ может быть сформулирована как задача построения такого множества покрытий единичных значений булевой функции, при котором сложность ДНФ будет минимальной.
Графически это означает, что необходимо и достаточно найти множество покрытий минимального ранга, представляющих множество единичных значений булевой функции.
МДНФ для рассматриваемой функции можно построить из трех интервалов второго ранга на пространственной решетке, что соответствует трем покрытиям 2-го ранга на карте Карно (рис.5.3., рис.5.4.).
f (x1,x2,x3) = x1x2 v 1 3 v x1 2x3 = 1 3 v x1x2 v x1x2x3 v x1x2 3 v x1 2x3 = 1 3 v x1x2 v x1x2 3 v x1x3(x2 v 2) = 1 3 v x1x2 v x1x3 = x1x2 v x1x3 v 1 3.
f (x1,x2,x3) = x1x2 v x1x3 v 1 3.
|
|
|
В правильности графического способа минимизации легко убедиться, выполнив некоторые аналитические преобразования в соответствии с законами алгебры логики.
Построение МДНФ является неоднозначным процессом, так как для данной функции может существовать несколько МДНФ, и сам процесс выбора покрытий строго не формализован. Графический метод хорошо работает для логических функций первой группы и в принципе, может применяться для функций 3-й группы, что вполне приемлемо в инженерной практике.
5.2. Метод минимизации Квайна
Метод представляет собой локальный алгоритм, включающий определенную последовательность этапов.
Этап 1. Нахождение первичных импликант.
Импликантой некоторой булевой функции называется другая булева функция, такая что множество нулевых значений импликанты Nимп.(0) пересекается со множеством нулевых значений функции Nf (0), а множество единичных значений Nимп.(1) принадлежит Nf (1).
Первичной импликантой булевой функции называется такая импликанта, никакая часть которой не является импликантой исходной функции. На данном этапе рассматриваются все элементарные конъюнкции (ЭК) ранга n, первоначально входящие в СДНФ. Они попарно сравниваются между собой с целью нахождения поглощений вида:
Fxi v F i = F,
при которых получаются ЭК ранга (n – 1). После получения всех возможных ЭК ранга (n – 1) они вновь сравниваются попарно между собой для получения ЭК ранга (n – 2) и т.д. ЭК, принявшие участие в поглощениях, отмечаются некоторым символом. Процесс заканчивается тогда, когда полученные ЭК ранга m не склеиваются между собою. Все не отмеченные ЭК бдут являться первичными импликантами. (Для данного построения целесообразно использовать квадратные таблицы, размерностью l x l, где l – число ЭК k-го ранга; k = n, n – 1, ..., m.)
Например:
f (x1, x2, x3, x4, x5) = 1 2 3 4x5 v 1 2 3x4x5 v 1 2x3x4x5 v 1x2 3 4 5 v 1x2 3x4x5 v 1x2x3 4 5 v 1x2x3 4x5 v x1 2 3x4 5 v x1 2 3x4x5 v x1x2 3 4 5 v x1x2 3 4x5 v x1x2 3x4 5 v x1x2 3x4x5
Таблица исходных ЭК ранга 5 примет вид (табл.5.1.).
Выписываем ЭК 5-го ранга:
* 1 2 3 4x5, * 1 2 3x4x5, * 1 2x3x4x5, * 1x2 3 4 5, * 1x2 3x4x5, * 1x2x3 4 5, * 1x2x3 4x5, *x1 2 3x4 5, *x1 2 3x4x5, *x1x2 3 4 5, *x1x2 3 4x5, *x1x2 3x4 5, *x1x2 3x4x5
Образуем ЭК n-го ранга путем просмотра списка слева направо и попарного сравнения:
1 2 3x5, 1 2x4x5, * 1 3x4x5, * 2 3x4x5, 1x2 4 5, x2 3 4 5, *x2 3x4x5, 1x2x3 4, *x1 2 3x4, *x1 3x4 5, *x1 3x4x5, *x1x2 3 4, *x1x2 3 5, *x1x2 3x5, *x1x2 3x4
ЭК, принявшие участие в склеивании, помечаем знаком *.
Далее строим ЭК 3-го ранга:
3x4x5, 3x4x5, x1 3x4, x1x2 3, x1x2 3
Повторяющиеся ЭК исключаем из дальнейшего рассмотрения:
3x4x5, x1 3x4, x1x2 3
Образовать ЭК 2-го ранга невозможно, следовательно первичными импликантами являются:
1 2 3x5, 1 2x4x5, 1x2 4 5, x2 3 4 5, 1x2x3 4, 3x4x5, x1 3x4, x1x2 3
Этап 2. Расстановка меток и нахождение существенных импликант.
В результате выполнения первого этапа минимизируемая функция оказалась представленной в виде:
f(x1,x2,...,xn)=![]()
где li – первичные импликанты.
Для нахождения минимальной формы необходимо исключить некоторые первичные импликанты. Поэтому составляется таблица, строки которой соответствуют первичным импликантам, а столбцы ЭК исходной функции. Если в некоторую ЭК входит одна из первичных импликант, то на пересечении соответствующей строки и столбца ставится метка. Если после заполнения всей таблицы в некотором столбце оказывается только одна метка, то первичная импликанта, находящаяся в данной строке, называется существенной (табл. 5.1.).
В нашем случае существенными импликантами являются:
1 2 3x5, 1 2x4x5, 1x2x3 4, 3x4x5, x1 3x4, x1x2 3
Из таблицы исключаются строки, соответствующие существенным импликантам, и столбцы ЭК, покрываемых этими существенными импликантами (табл.5.1.).
Этап 3. Вычеркивание избыточных столбцов и избыточных первичных импликант.
Если в таблице, полученной на предыдущем этапе, имеются столбцы, в которых метки расположены в одинаковых строках, то один из таких столбцов вычеркивается. Так как покрытие оставшегося столбца будет осуществлять покрытие удаленной ЭК.
Если после удаления избыточных столбцов в таблице появляются строки, в которых нет ни одной метки, то они вычеркиваются, так как первичные импликанты, соответствующие этим строкам не покрывают оставшиеся в рассмотрении ЭК.
В нашем примере избыточные строки и столбцы отсутствуют.
Таблица 5.1.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 3x5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2x4x5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1x2 4 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 3 4 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1x2x3 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3x4x5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 3x4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x1x2 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 5.2.
|
B1 |
1x2 4 5 |
|
x2 3 4 5 |
|
A1= 1 2 3 4x5;A2= 1 2 3x4x5;A3= 1 2x3x4x5;A4= 1x2 3 4 5;A5= 1x2 3x4x5;A6= 1x2x3 4 5; A7= 1x2x3 4x5;A8=x1x2 3x4 5;A9=x1 2 3x4x5;A10=x1x2 3 4 5;A11=x1x2 3 4x5;A12=x1x2 3x4 5; A13=x1x2 3x4x5;
B1= 1x2 3 4 5.
Этап 4. Выбор минимального покрытия максимальными интервалами.
Из таблицы, полученной в результате выполнения третьего этапа, выбирается такая совокупность первичных импликант, которая включает хотя бы по одной метке в каждом столбце. При нескольких возможных вариантах выбирается покрытие минимальной сложности.
В рассматриваемом примере остается выбрать одну из первичных импликант.
Результатом минимизации будет МДНФ:
1
2
3x5,
1
2x4x5,![]() 1x2x3
4,
x2
3
4
5,
3x4x5,
x1
3x4,
x1x2
3.
1x2x3
4,
x2
3
4
5,
3x4x5,
x1
3x4,
x1x2
3.

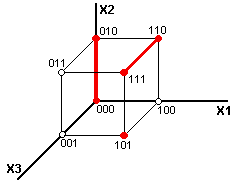 Рис.
5.1.
Рис.
5.1.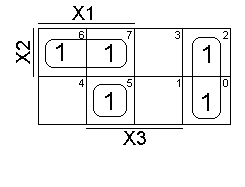
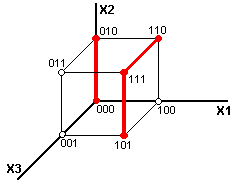 Рис.
5.3.
Рис.
5.3.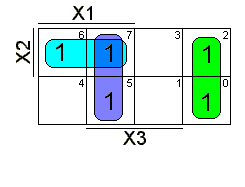 Рис.
5.4.
Рис.
5.4.