Поиск решения

Команда Подбор параметра является удобной для решения задач поиска определенного целевого значения, зависящего от одного неизвестного параметра. Для более сложных задач следует использовать команду Поиск решения (Решатель), доступ к которой реализован через пункт меню Сервис/Поиск решения.

Задачи, которые можно решать с помощью Поиска решения, в общей постановке формулируются так:

Найти: х₁, х₂, … , х_n такие, что: F(х₁, х₂, … , х_n) > {Max; Min; = Value} при ограничениях: G(х₁, х₂, … , х_n) > { Value;  Value; = Value}

Искомые переменные - ячейки рабочего листа Excel - называются регулируемыми ячейками. Целевая функция F(х₁, х₂, … , х_n), называемая иногда просто целью, должна задаваться в виде формулы в ячейке рабочего листа. Эта формула может содержать функции, определенные пользователем, и должна зависеть (ссылаться) от регулируемых ячеек. В момент постановки задачи определяется, что делать с целевой функцией. Возможен выбор одного из вариантов:

• найти максимум целевой функции F(х₁, х₂, … , х_n);

• найти минимум целевой функции F(х₁, х₂, … , х_n);

• добиться того, чтобы целевая функция F(х₁, х₂, … , х_n) имела фиксированное значение: F(х₁, х₂, … , х_n) = a.

Функции G(х₁, х₂, … , х_n) называются ограничениями. Их можно задать как в виде равенств, так и неравенств. На регулируемые ячейки можно наложить дополнительные ограничения: неотрицательности и/или целочисленности, тогда искомое решение ищется в области положительных и/или целых чисел.

Под эту постановку попадает самый широкий круг задач оптимизации, в том числе решение различных уравнений и систем уравнений, задачи линейного и нелинейного программирования. Такие задачи обычно проще сформулировать, чем решать. И тогда для решения конкретной оптимизационной задачи требуется специально для нее сконструированный метод. Решатель имеет в своем арсенале мощные средства решения подобных задач: метод обобщенного градиента, симплекс-метод, метод ветвей и границ.

Выше для нахождения корней квадратного уравнения был применен метод Ньютона (п. 1.4) с использованием циклических ссылок (п. 2.1) и средство Подбор параметра (п. 2.2). Рассмотрим, как воспользоваться Поиском решения на примере того же квадратного уравнения.

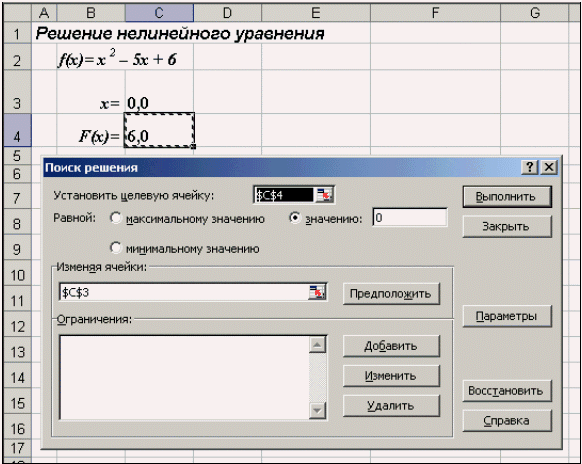
Рис. 12. Окно диалога Поиск решения

После открытия диалога Поиск решения (рис. 12) необходимо выполнить следующие действия:

1. в поле Установить целевую ячейку ввести адрес ячейки, содержащей формулу для вычисления значений оптимизируемой функции, в нашем примере целевая ячейка - это С4, а формула в ней имеет вид: = C3^2 - 5*C3 + 6;

2. для максимизации значения целевой ячейки, установить переключатель максимальному значению в положение , для минимизации используется переключатель минимальному значению, в нашем случае устанавливаем переключатель в положение значению и вводим значение 0;

3. в поле Изменяя ячейки ввести адреса изменяемых ячеек, т.е. аргументов целевой функции (С3), разделяя их знаком ";" (или щелкая мышью при нажатой клавише Сtrl на соответствующих ячейках), для автоматического поиска всех влияющих на решение ячеек используется кнопка Предположить;

4. в поле Ограничения с помощью кнопки Добавить ввести все ограничения, которым должен отвечать результат поиска: для нашего примера ограничений задавать не нужно;

5. для запуска процесса поиска решения нажать кнопку Выполнить.

Рис. 13. Результаты поиска

Для сохранения полученного решения необходимо использовать переключатель Сохранить найденное решение в открывшемся окне диалога Результаты поиска решения. После чего рабочий лист примет вид, представленный на рис. 13. Полученное решение зависит от выбора начального приближения, которое задается в ячейке С4 (аргумент функции). Если в качестве начального приближения в ячейку С4 ввести значение, равное 1,0, то с помощью Поиска решения найдем второй корень, равный 2,0.

Опции, управляющие работой Поиска решения, задаваемые в окне Параметры (окно появляется, если нажать на кнопку Параметры окна Поиск решения), следующие (рис. 14):

Рис. 14. Настройка параметров Решателя

• Максимальное время - ограничивает время, отведенное на процесс поиска решения (по умолчанию задано 100 секунд, что достаточно для задач, имеющих около 10 ограничений, если задача большой размерности, то время необходимо увеличить).

• Предельное число итераций - еще один способ ограничения времени поиска путем задания максимального числа итераций. По умолчанию задано 100, и, чаще всего, если решение не получено за 100 итераций, то при увеличении их количества (в поле можно ввести время, не превышающее 32767 секунд) вероятность получить результат мала. Лучше попытаться изменить начальное приближение и запустить процесс поиска заново.

• Относительная погрешность - задает точность, с которой определяется соответствие ячейки целевому значению или приближение к указанным ограничениям (десятичная дробь от 0 до 1).

• Допустимое отклонение - задается в % только для задач с целочисленными ограничениями. Поиск решения в таких задачах сначала находит оптимальное нецелочисленное решение, а потом пытается найти ближайшую целочисленную точку, решение в которой отличалось бы от оптимального не более, чем на указанное данным параметром количество процентов.

• Сходимость - когда относительное изменение значения в целевой ячейке за последние пять итераций становится меньше числа (дробь из интервала от 0 до 1), указанного в данном параметре, поиск прекращается.

• Линейная модель - этот флажок следует включать, когда целевая функция и ограничения - линейные функции. Это ускоряет процесс поиска решения.

• Неотрицательные значения - этим флажком можно задать ограничения на переменные, что позволит искать решения в положительной области значений, не задавая специальных ограничений на их нижнюю границу.

• Автоматическое масштабирование - этот флажок следует включать, когда масштаб значений входных переменных и целевой функции и ограничений отличается, возможно, на порядки. Например, переменные задаются в штуках, а целевая функция, определяющая максимальную прибыль, измеряется в миллиардах рублей.

• Показывать результаты итераций - этот флажок позволяет включить пошаговый процесс поиска, показывая на экране результаты каждой итерации.

• Оценки - эта группа служит для указания метода экстраполяции - линейная или квадратичная, - используемого для получения исходных оценок значений переменных в каждом одномерном поиске. Линейная служит для использования линейной экстраполяции вдоль касательного вектора. Квадратичная служит для использования квадратичной экстраполяции, которая дает лучшие результаты при решении нелинейных задач.

• Разности (производные) - эта группа служит для указания метода численного дифференцирования, который используется для вычисления частных производных целевых и ограничивающих функций. Параметр Прямые используется в большинстве задач, где скорость изменения ограничений относительно невысока. Параметр Центральные используется для функций, имеющих разрывную производную. Данный способ требует больше вычислений, однако его применение может быть оправданным, если выдается сообщение о том, что получить более точное решение не удается.

• Метод поиска - служит для выбора алгоритма оптимизации. Метод Ньютона был рассмотрен ранее. В Методе сопряженных градиентов запрашивается меньше памяти, но выполняется больше итераций, чем в методе Ньютона. Данный метод следует использовать, если задача достаточно велика и необходимо экономить память, а также если итерации дают слишком малое отличие в последовательных приближениях.

Сохранить модель поиска решения можно следующими способами:

1. при сохранении книги Excel после поиска решения все значения, введенные в окнах диалога Поиск решения, сохраняются вместе с данными рабочего листа. С каждым рабочим листом в рабочей книге можно сохранить один набор значений параметров Поиска решения;

2. если в пределах одного рабочего листа Excel необходимо рассмотреть несколько моделей оптимизации (например найти максимум и минимум одной функции, или максимальные значения нескольких функций), то удобнее сохранить эти модели, используя кнопку Параметры/Сохранить модель окна Поиск решения. Диапазон для сохраняемой модели содержит информацию о целевой ячейке, об изменяемых ячейках, о каждом из ограничений и все значения диалога Параметры. Выбор модели для решения конкретной оптимизационной задачи осуществляется с помощью кнопки Параметры/Загрузить модель диалога Поиск решения;

3. еще один способ сохранения параметров поиска - сохранение их в виде именованных сценариев. Для этого необходимо нажать на кнопку Сохранить сценарий диалогового окна Результаты поиска решений.

Кроме вставки оптимальных значений в изменяемые ячейки Поиск решения позволяет представлять результаты в виде трех отчетов: Результаты, Устойчивость и Пределы. Для генерации одного или нескольких отчетов необходимо выделить их названия в окне диалога Результаты поиска решения. Рассмотрим более подробно каждый из них.

Рис. 15. Отчет по устойчивости

Отчет по устойчивости (рис.15) содержит информацию о том, насколько целевая ячейка чувствительна к изменениям ограничений и переменных. Этот отчет имеет два раздела: один для изменяемых ячеек, а второй для ограничений. Правый столбец в каждом разделе содержит информацию о чувствительности. Каждая изменяемая ячейка и ограничения приводятся в отдельной строке. Раздел для изменяемых ячеек содержит значение нормированного градиента, которое показывает, как целая ячейка реагирует на увеличение значения в соответствующей изменяемой ячейке на одну единицу. Подобным образом, множитель Лагранжа в разделе для ограничений показывает, как целевая ячейка реагирует на увеличение соответствующего значения ограничения на одну единицу. При использовании целочисленных ограничений Excel выводит сообщение Отчеты устойчивость и Пределы не применимы для задач с целочисленными ограничениями. Если в окне диалога Параметры поиска решения установлен флажок Линейная модель, то отчет по устойчивости содержит несколько дополнительных столбцов информации.

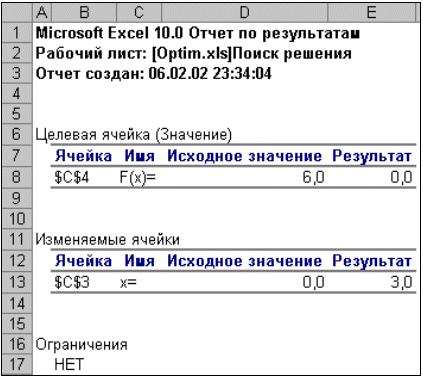
Рис. 16. Отчет по результатам

Отчет по результатам (рис.16) содержит три таблицы: в первой приведены сведения о целевой функции до начала вычисления, во второй - значения искомых переменных, полученные в результате решения задачи, в третьей - результаты оптимального решения для ограничений. Этот отчет также содержит информацию о таких параметрах каждого ограничения, как статус и разница. Статус может принимать три состояния: связанное, несвязанное или невыполненное. Значение разницы - это разность между значением, выводимым в ячейке ограничения при получении решения, и числом, заданным в правой части формулы ограничения. Связанное ограничение - это ограничение, для которого значение разницы равно нулю. Несвязанное ограничение - это ограничение, которое было выполнено с ненулевым значением разницы.

Отчет по пределам содержит информацию о том, в каких пределах значения изменяемых ячеек могут быть увеличены или уменьшены без нарушения ограничений задачи. Для каждой изменяемой ячейки этот отчет содержит оптимальное значение, а также наименьшие значения, которые ячейка может принимать без нарушения ограничений.

 

БИЛЕТ 20

Постановка задачи аппроксимации функции одной переменной

Пусть в результате измерений в процессе опыта получено табличное задание некоторой функции f(х), выражающей связь между двумя географическими параметрами:

 

(1)

х	x1	х2	…	xn
f(x)	y1	у2	…	yn

 

Конечно, можно найти формулу, выражающую эту зависимость аналитически, применив метод интерполяции. Однако, совпадение значений полученного аналитического задания функции в узлах интерполяции с имеющимися эмпирическими данными часто может вовсе не означать совпадение характеров поведения исходной и интерполирующей функции на всем интервале наблюдения. Кроме того, табличная зависимость географических показателей всегда получается в результате измерений различными приборами, имеющими определенную и не всегда достаточно малую погрешность измерения. Требование точного совпадения значений приближающей и приближаемой функций в узлах является тем более неоправданным, если значения функции f(х), полученные в результате измерений уже сами являются приближенными.

Задача аппроксимации функции одной переменной с самого начала обязательно учитывает характер поведения исходной функции на всем интервале наблюдений. Формулировка задачи выглядит следующим образом. Функция у= f(х) задана таблицей (1). Необходимо найти функцию заданного вида:

y=F(x)                                               (2)

которая в точках x₁, x₂, …, x_n принимает значения, как можно более близкие к табличным y₁, y₂, …, y_n.

На практике вид приближающей функции чаще всего определяют путем сравнения вида приближенно построенного графика функции у= f(х) с графиками известных исследователю функций, заданных аналитически (чаще всего простых по виду элементарных функций). А именно, по таблице (1) строится точечный график f(x), затем проводится плавная кривая, по возможности наилучшим образом отражающая характер расположения точек. По полученной таким образом кривой на качественном уровне устанавливается вид приближающей функции.

Рассмотрим рисунок 6.

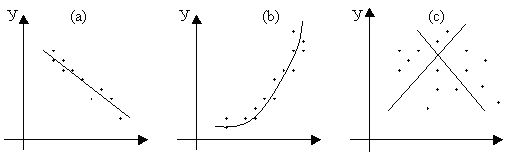
Рис. 6

На рисунке 6 изображены три ситуации:

• На графике (а) взаимосвязь х и у близка к линейной; прямая линия здесь близка к точкам наблюдений, и последние отклоняются от нее лишь в результате сравнительно небольших случайных воздействий.

• На графике (b) реальная взаимосвязь величин х и у описывается нелинейной функцией, и какую бы мы ни провели прямую линию, отклонение точек наблюдения от нее будет существенным и неслучайным. В то же время, проведенная ветка параболы достаточно хорошо отражает характер зависимости между величинами.

• На графике (с) явная взаимосвязь между переменными х и у отсутствует; какую бы мы ни выбрали формулу связи, результаты ее параметризации будут здесь неудачными. В частности, обе выбранные прямые одинаково плохи для того, чтобы делать выводы об ожидаемых значениях переменной у по значениям переменной х.

Следует заметить, что строгая функциональная зависимость для таблицы исходных данных наблюдается редко, ибо каждая из участвующих в ней величин может зависеть от многих случайных факторов. Однако формула (2) (ее называют эмпирической формулой или уравнением регрессии у на х) интересна тем, что позволяет находить значения функции f для нетабличных значений х, "сглаживая" результаты измерений величины у, т.е. на всем интервале изменения х. Оправданность такого подхода определяется в конечном счете практической полезностью полученной формулы.

Интерполяция – один из способов аппроксимации данных. В простейшем (одномерном) случае задача интерполяции [1-3] состоит в следующем: заданы точки (x_i, y_i), и требуется найти функцию (x), которая проходит через эти точки (см. рис. 1),

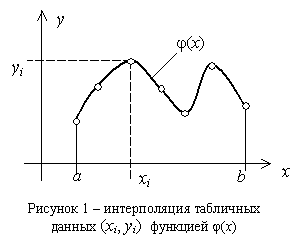
т.е.

(x_i)= y_i , .                (1)                  

Точки (x_i, y_i) называют узлами интерполяции, а функцию (x) – интерполирующей функцией или интерполянтом. Вид функции (x) определяет способ интерполяции. На практике в качестве интерполирующей функции (x) часто используются алгебраические полиномы различного вида, так как полиномы легко вычислять, дифференцировать и интегрировать. При этом интерполяция носит название полиномиальной.

Рассмотрим задачу линейной интерполяции. При этом интерполирующая функция имеет следующий вид:

,      (2)

где ₀(x),  ₁(x), … ,  _m(x) – базисные функции.

Используя условие (1) и выражение (2), получаем систему уравнений

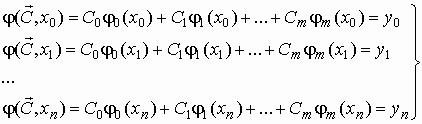        (3)

Единственное решение системы (3) существует при двух условиях:

1. число точек (x_i, y_i), 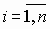равно числу коэффициентов С_k,  ;

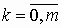2. система уравнений (3) должна быть невырожденной, т.е. определитель системы .

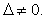Таким образом, если выполняются вышеуказанные условия, то через точки (x_i, y_i) проходит единственная функция .

В случае линейной полиномиальной интерполяции базисные функции имеют следующий вид: ₀(x)= x⁰=1,  ₁(x)= x¹=x,   ₂(x)= x², … ,  _m(x)= x^m. Интерполирующая функция при этом имеет вид полинома степени m: (x)= P_m(x)=C₀ + C₁ x + C₂ x ² + … +C_m x ^m и, следовательно, система (3) примет вид

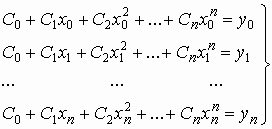         (4)

В матричной форме систему (4) можно переписать как А*C=B, где

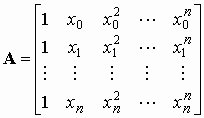– матрица Ван дер Монда; ; .

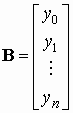Решением системы (4) будет вектор коэффициентов полинома С. Так как определитель матрицы Ван дер Монда всегда отличен от нуля (при x_i x_j), то решение системы (4) – единственное. Для решения системы (4) необходимо найти обратную матрицу A. В этом случае решением (4) будет C=A^–1*B.

 

Вывод: Таким образом, через заданные на интервале [a, b] точки (x_i, y_i), всегда можно провести единственный интерполяционный полином (x)=P_n(x)=C₀ + C₁ x + + C₂ x² + … +C_n x ⁿ, коэффициенты которого находятся в результате решения системы (4).

Выражение (1) определяет поведение функции (x) только в узлах интерполяции (x_i, y_i), . Между узлами (x) может вести себя произвольным образом, сколь угодно далеко, в принципе, отклоняясь от зависимости f(x). Определить погрешность приближения можно, используя выражение для абсолютной ошибки =| f(x) – (x) |.

 

Ошибка полиномиальной интерполяции. Лучший способ проверить качество интерполяции – вычислить значения интерполирующей функции в большом числе точек и построить график. Однако в некоторых ситуациях качество интерполянта можно проанализировать. Предположим, что величина y_i представляет собой точные значения известной функции f(x) в точках x_i. Пусть P_n(x) – единственный полином n-й степени, интерполирующий функцию по этим точкам (x_i, y_i), . Предположим, что во всех точках х [a, b] функция f(x) имеет (n+1) непрерывную производную. Тогда можно показать [1, 2], что абсолютная ошибка интерполяции (x)=| f(x)– P_n(x) | определяется выражением

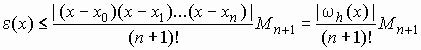,          (5)

где - максимальное значение (n+1)-й производной функции f(x) на интервале [a, b]; .

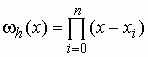Теперь посмотрим, что получится, если интерполировать известную функцию f(x) все в большем и большем числе точек на фиксированном интервале. Выражение для погрешности (5) состоит из трех разных частей; факториал и произведение разностей с увеличением n уменьшают ошибку, но порядок производной при этом растет. Для многих функций величина M_n+1 увеличиваются быстрее, чем (n+1)!. В результате полиномиальные интерполянты редко сходятся к обычной непрерывной функции. Практический эффект выражается в том, что интерполирующий полином высокой степени может вести себя "плохо" в точках, отличных от узлов интерполяции (x_i, y_i), . Поэтому на практике часто используют интерполянты степени не выше 5-6.

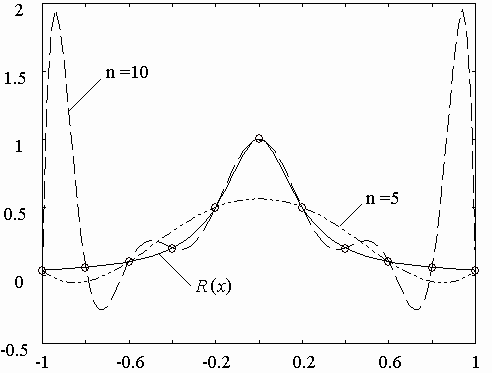
Рисунок 2 – интерполяция функции Рунге полиномом степени n

Примером может служить функция Рунге [4] вида R(x)=1/(1+25x²), график которой представлен на рис. 2. С увеличением порядка интерполирующего полинома при равномерном распределении узлов интерполяции на интервале [–1, 1] происходит ухудшение качества приближения на краях интервала. Это объясняется тем, что производные R(x), которые фигурируют в выражении для погрешности интерполяции (5), быстро растут с увеличением числа n.

 

Точность приближения зависит не только от числа узлов интерполяции (т.е. порядка интерполирующего полинома), но и от их расположения на интервале [a, b]. В простейшем случае выбирается равномерное расположение точек (x_i, y_i), на интервале [a, b] с шагом x=(b–a)/(n–1). Однако, как показывает практика, равномерное расположение не является оптимальным с точки зрения лучшего приближения j (x) к зависимости f(x). Более оптимальным для полиномиальной интерполяции является расположение узлов на интервале [a, b] по формуле Чебышева

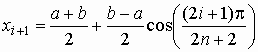, .          (6)

Выражение (6) определяет так называемое оптимальное распределение узлов интерполяции на интервале [a, b].

ИЛИ

2.1. Постановка задачи интерполяции.

Пусть известные значения некоторой функции f образуют следующую таблицу:

 

х	x0	x1	…	xn
f(x)	y0	y1	…	yn

При этом требуется получить значение функции f для такого значения аргумента х, которое входит в отрезок [x₀;x_n], но не совпадает ни с одним из значений x_i (i=0,1,…,n).

Классический подход к решению задачи построения приближающей функции основывается на требовании строгого совпадения значений f(x) и F(x) в точках x_i(i=0, 1, 2, …, n), т.е.

F(x₀)=y₀, F(x₁)=y₁, …, F(x_n)=y_n.                              (1)

В этом случае нахождение приближенной функции называют интерполяцией (или интерполированием), а точки x₀, x₁, …, x_n – узлами интерполяции. Геометрически это означает, что нужно найти кривую y=F(x) некоторого определенного типа, проходящую через заданную систему точек M_i(x_i,y_i) (i=0,1,2,…,n) (рис. 1). В случае, если x [x₀, x_n] нахождение искомой функции называют экстраполяцией. В дальнейшем, под термином интерполяция будем понимать как первую, так и вторую операции.

 

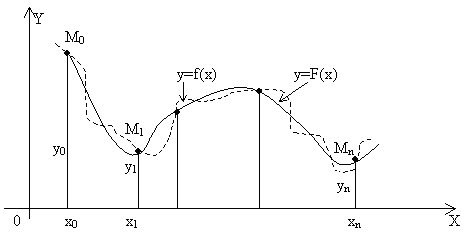
Рис. 1

Задача интерполирования может иметь в общей постановке бесчисленное множество решений или совсем их не иметь. Однако эта задача становится однозначной, если вместо произвольной функции F(x) искать некоторую функцию конкретного вида, удовлетворяющую условиям (1).

Наиболее удобной в практическом использовании функцией является алгебраический многочлен степени n :

P_n(x)=a₀xⁿ + a₁x^n-1 + … + a_n-1x + a_n

Чтобы задать многочлен n-ой степени достаточно задать его n+1 коэффициент. Значения многочлена просто вычисляются, его легко продифференцировать, проинтегрировать и т.д. Поэтому алгебраические многочлены нашли широкое применение для приближения функций.

Ниже будут подробно изложены широко используемые в географических исследованиях случаи интерполяции линейной функцией (линейная интерполяция) и квадратичной функцией (квадратичная интерполяция). Подробно с методами интерполяции функции полиномами можно познакомиться в [13] .

БИЛЕТ 21

Линейная интерполяция.

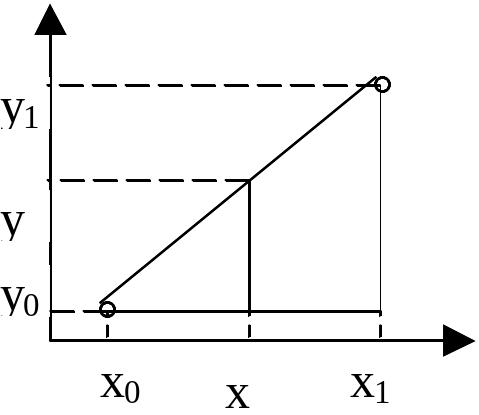
Линейная интерполяция состоит в том, что заданные точки (x_i,y_i) соединяются прямолинейными отрезками, и функция f(x) приближается ломаной с вершинами в заданных точках. Рассмотрим два подобных прямоугольных треугольника, имеющих общую вершину в точке (x_i,y_i).

tg  = (y1–y0)/(x1–x0) = (y–y0)/(x–x0) y–y0 = (x–x0)·(y1–y0)/(x1–x0) y = y0+(x–x0)·(y1–y0)/(x1–x0) h=x1-x0 y=y0+(x-x0)(y1-y0)/h

Расчетные формулы линейной интерполяции.

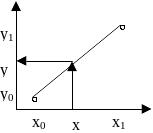
h=x₁-x₀ y=y₀+(x-x₀)(y₁-y₀)/h

Квадратичная интерполяция.

Расчетные формулы для квадратичной интерполяции приведены для случая, когда таблица значений f(x) построена с постоянным шагом по x.

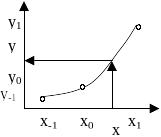
h=x₁-x₀=x₀x_-1

p=(x-x₀)/h

y=p(p-1)y_-1/2+(1-p²)y₀+p(p+1)y₁/2

2.2. Линейная интерполяция.

Итак, пусть мы имеем функцию, заданную таблично. Решая задачу интерполяции, найдем в таблице два соседних значения аргумента (обозначим их х_k и x_k+1), между которыми лежит заданное значение х (х_k <x<x_k+1), пусть y_k=f(x_k) и y_k+1=f(x_k+1) – соответствующие им значения функции. Будем считать, что в промежутке (х_k , x_k+1) данную функцию с достаточной степенью точности можно заменить линейной функцией, т.е. дугу графика функции можно заменить стягивающей ее хордой (рис.2). Такая замена называется линейной интерполяцией.

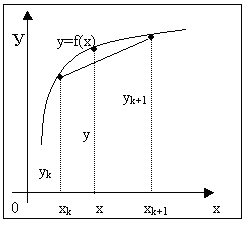
Рис. 2

Уравнение прямой, проходящей, через точки (х_k , y_k) и (х_k+1 , y_k+1), имеет следующий вид:

или в более привычной форме уравнения с угловым коэффициентом:

Применение линейной интерполяции для приближенного вычисления значений функции обосновано в том случае, когда возникающая при этом погрешность невелика. Для нахождения погрешности обозначим разность между неизвестным нам точным значением функции f(x) и ее приближенным значением, определяемым формулой (1) через (х):

Будем предполагать также, что вторая производная функции f(x) на рассматриваемом участке непрерывна и удовлетворяет неравенству

,

где .

Используя аппарат математического анализа можно доказать [27], что для любого х из интервала (x_k, x_k+1) оценка погрешности линейной интерполяции будет иметь следующий вид:

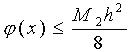
Заметим, что вторая производная функции f(x) имеет конкретный механический смысл. Если f(x) описывает закон движения материальной точки, то вторая производная этой функции задает ускорение этой точки в момент времени х. Факт существования ограничения на ускорение (ограниченность второй производной) с физической точки зрения означает, что процесс описываемый функцией f(x) протекает относительно равномерно и функция изменяется не очень быстро. Таковой, например, будет функция, задающая изменение суточной температуры воздуха от времени. На практике именно этим критерием "плавности" скорости изменения процесса можно вполне воспользоваться для ответа на вопрос об обоснованности применения линейной интерполяции.

Окончательно линейная интерполяция считается применимой, если вносимая ею дополнительная погрешность заметно меньше погрешности измерений натурных данных. Если обозначить через m номер последнего разряда приводимых в таблице значений функции, то погрешность измерений будет равна

и условие применимости линейной интерполяции запишется в виде неравенства:

         (2)

Шаг и точность таблицы обычно стараются согласовать так, чтобы условие (2) было выполнено.

Бывает, однако, что для выполнения этого условия требуется выбирать слишком малый шаг. В таком случае не считаются с этим условием, а для отыскания промежуточных значений функции пользуются более сложной квадратичной интерполяцией или другими приемами [17].

 

2.3.Квадратичная интерполяция.

Пусть снова дана функция f(x), заданная таблично. Считая, что на промежутке (x_k, x_k+2) данную функцию с достаточной степенью точности можно заменить квадратичной функцией, то есть часть графика функции можно заменить параболой (см. рис. 3), необходимо найти значение функции f(x) в некоторой точке x, принадлежащей интервалу (x_k, x_k+2).

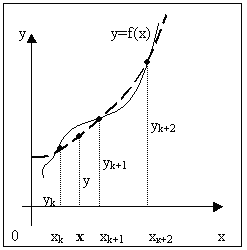
Рис. 3

Будем искать квадратичную функцию в следующем виде: .

Исходя из условия совпадения значений искомой квадратичной функции с табличными значениями функции в трех заданных точках, составим следующую систему уравнений:

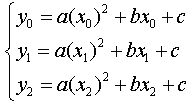
Это система трех линейных уравнений с тремя неизвестными a, b и с. Ее определитель не равен 0 (если только точки не лежат на одной прямой). Решая составленную систему уравнений матричным способом, получим следующую зависимость для коэффициентов а, b и с:

Таким образом значение функции f(х) в точке х можно приближенно считать равным

 

Естественно поставить вопрос о погрешности полученной формулы.

Рассмотрим разность между точным значением функции f(х) и ее приближенным значением. Обозначим эту разность через (х):

(х)= f(х)-ax²-bx-c.

Мы подошли к задаче об оценке значений функции j (х) для х, пробегающих промежуток (х_к, х_к+2).

В рассматриваемом случае нам придется предполагать, что третья производная функции f(х) на рассматриваемом промежутке непрерывна и удовлетворяет неравенству [27]:

.

Тогда для (х) справедлива следующая оценка:

БИЛЕТ 24

Метод наименьших квадратов

Через имеющееся "облако" точек всегда можно попытаться провести линию установленного вида, которая является наилучшей в определенном смысле среди всех линий данного вида, то есть "ближайшей" к точкам наблюдений по их совокупности. Для этого определим вначале понятие близости линии к некоторому множеству точек на плоскости. Меры такой близости могут быть различными [13]. Однако, любая разумная мера должна быть, очевидно, связана с расстоянием от точек наблюдения до рассматриваемой линии (задаваемой уравнением y=F(x)).

Предположим, что приближающая функция F(x) в точках х₁, x₂, ..., x_n имеет значения y₁, y₂, ..., y_n. Часто в качестве критерия близости используется минимум суммы квадратов разностей наблюдений зависимой переменной y_i и теоретических, рассчитанных по уравнению регрессии значений y_i. Здесь считается, что y_i и x_i - известные данные наблюдений, а F - уравнение линии регрессии с неизвестными параметрами (формулы для их вычисления будут приведены ниже). Метод оценивания параметров приближающей функции, минимизирующий сумму квадратов отклонений наблюдений зависимой переменной от значений искомой функции, называется методом наименьших квадратов (МНК) или Least Squares Method (LS).

Итак, задачу приближения функции f теперь можно сформулировать следующим образом: для функции f, заданной таблицей (1), найти функцию F определенного вида так, чтобы сумма квадратов Ф была наименьшей.

Рассмотрим метод нахождения приближающей функции в общем виде на примере аппроксимирующей функции с тремя параметрами:

                                (3)

Пусть F(x_i, a, b, c) = y_i, i=1, 2, ..., n. Сумма квадратов разностей соответствующих значений f и F будет иметь вид:

                          (4)

Эта сумма является функцией Ф(а, b, c) трех переменных (параметров a, b и c). Задача сводится к отысканию ее минимума. Используем необходимое условие экстремума:

Получаем систему для определения неизвестных параметров a, b, c.

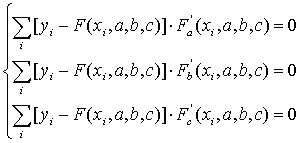                         (5)

Решив эту систему трех уравнений с тремя неизвестными относительно параметров a, b, c, мы и получим конкретный вид искомой функции F(x, a, b, c). Как видно из рассмотренного примера, изменение количества параметров не приведет к искажению сущности самого подхода, а выразится лишь в изменении количества уравнений в системе (5).

Естественно ожидать, что значения найденной функции F(x, a, b, c) в точках х₁, x₂, ..., x_n, будут отличаться от табличных значений y₁, y₂, ..., y_n. Значения разностей y_i-F(x_i,a, b, c)=e _i (i=1, 2, ..., n) называются отклонениями измеренных значений y от вычисленных по формуле (3). Для найденной эмпирической формулы (2) в соответствии с исходной таблицей (1) можно, следовательно найти

сумму квадратов отклонений , которая в соответствии с методом наименьших квадратов для заданного вида приближающей функции (и найденных значений параметров) должна быть наименьшей. Из двух разных приближений одной и той же табличной функции, следуя методу наименьших квадратов, лучшим нужно считать то, для которого сумма (4) имеет наименьшее значение.

В экспериментальной практике в качестве приближающих функций в зависимости от характера точечного графика f часто используются приближающие функции с двумя параметрами:

Очевидно, что когда вид приближающей функции установлен, задача сводится только к отысканию значений параметров.

БИЛЕТ 27

При проведении сложного статистического или инженерного анализа можно упростить процесс и сэкономить время, используя надстройку «Пакет анализа». Для анализа данных с помощью этого пакета следует указать входные данные и выбрать параметры; расчет будет выполнен с помощью подходящей статистической или инженерной макрофункции, а результат будет помещен в выходной диапазон. Некоторые инструменты позволяют представить результаты анализа в графическом виде.

ИЛИ

Финансовые функции

Финансовые функции применяются при планировании и анализе финансово-хозяйственной деятельности предприятия, атакже при решении задач, связанных с инвестированием средств. Большинство финансовых функций доступно только после загрузки соответствующих надстроек. Среди финансовых функций можно выделить три больших блока функций, которые используются для расчета амортизационных отчислений, рентных платежей и доходов от ценных бумаг. Учитывая огромное практическое значение этих функций, в данной книге мы решили привести полный их перечень. В него включены и те функции, которые становятся доступными только после установки надстройки Пакет анализа.

для работы с несколькими выборками и углубленного анализа данных, называемый Пакет анализа, который может быть использован для решения задач статистической обработки выборочных данных.

Использование инструмента Пакет анализа для выявления различий между выборками

Составление прогнозов с помощью надстроек скользящего среднего

Другим способом применения скользящего среднего является использование надстройки Пакет анализа. Установить

Прогнозирование о помощью функций регрессии Ехсеl

БИЛЕТ 28

Физико-химическая модель дает описание химического состава геологической модели в терминах физико-химической системы. При использовании в физико-химической модели методов равновесной термодинамики она содержит термодинамические свойства образующихся соединений и необходимые для расчета термодинамических равновесий уравнения, а также - уравнения, описывающие кинетику реакций и динамику переносаљ вещества.

БИЛЕТ 31