3.1 Два типа задач решаемых на основе выборочного метода.

Выборочный метод используется для решения двух типов задач. Первый тип задач так или иначе связан с получением оценок параметров генеральной совокупности, а второй состоит в проверке на основе выборки некоторого предположения относительно генеральной совокупности. Первый тип и включает в себя три задачи: 1) установление границ, в которых с принятым доверительным уровнем вероятности находится параметр генеральной совокупности; 2)расчет минимально необходимой численности выборки, обеспечивающей появление ошибки не больше заданной; 3)определение уровня вероятности появления заданной ошибки при ограниченной численности выборки. Рассмотрим последовательность решения каждой из перечисленных задач на примере использования выборочного метода для оценки генеральной средней и доли

3.2 Интервальная оценка генеральной средней и доли. Данная задача решается в такой последовательности: 1) из генеральной совокупности осуществляется выборка численностью единиц; 2) по выборочной совокупности определяется выборочная средняя, как оценка для средней генеральной; при ее расчете может быть использована формула средней арифметической простой или (если выборочные данные представлены вариационным рядом распределения) средней арифметической взвешенной ; 3)по выборочной совокупности определяется значение выборочного среднего квадратического отклонения по формулам: ( для случая простой средней ) или ( для случая, когда выборочная средняя определяется как средняя взвешенная); 4) определяется средняя ошибка выборочной средней ; 5) устанавливается доверительный уровень вероятности (Р); 6) для принятого доверительного уровня вероятности по соответствующим таблицам находят значение коэффициента t ; 7) определяются границы предельной ошибки ; 8)с принятым доверительным уровнем вероятности генеральная средняя находится в интервале 0 = ± ;

Для интервальной оценки генеральной доли из генеральной совокупности формируется выборка численностью единиц, затем по выборке определяется число единиц ( с неким качеством. Соотношение - это оценка доли в генеральной совокупности, ее средняя ошибка будет равна . Для нахождения границ предельной ошибки для доли следует выбрать доверительный уровень вероятности - Р, по таблицам интеграла вероятностей нормального распределения (доля обычно оценивается на основе больших выборок) найти коэффициент t и , следовательно, границы предельной ошибки для доли составят . Определив возможные границы предельной ошибки можно установить с заданным уровнем вероятности границы доли признака в генеральной совокупности W =

3.3 Определение необходимой численности выборки

Эта задача решается в том случае, если значение ошибки (чаще всего предельной) заранее задано и, следовательно, стоит вопрос о том какова должна быть минимальная численность выборки, чтобы ошибка с принятым доверительным уровнем вероятности не выходила за заданные границы. Алгоритм решения этой задачи вытекает из формулы расчета предельной ошибки = . Из этого равенства вытекает, что . Необходимая численность выборки определяется округленно до целых единиц, округление при этом производится всегда в большую сторону.

При использовании представленной выше формулы возникает проблема с дисперсией - . Ведь, по сути, выборка еще не производилось, а величина ее дисперсии должна быть уже известна. Решается проблема двояким образом: если исследуемая генеральная совокупность подвергалась ранее выборочному наблюдению, то можно воспользоваться значением дисперсии по данным предшествующей выборки; если же выборочного наблюдения не было, то для установления дисперсии можно провести экспресс выборку и по ней рассчитать величину дисперсии.

Интервалы предельной ошибки весьма часто задаются в % от оценки, например, в % от выборочной средней. В этом случае формула для расчета минимально необходимой численности выборки будет выглядеть так: 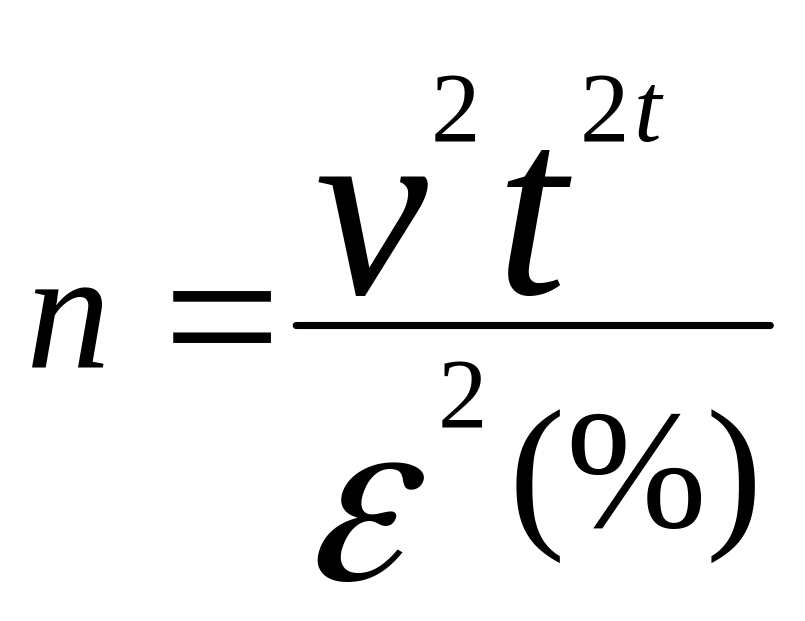, где - квадрат выборочного коэффициента вариации, - квадрат ошибки , выраженной в %.