Нормальна форма матриці. Діагональна і жорданова форми матриць.
Жорданова нормальна форма матриць.
Хай
,
.Поняття
Жорданової клітини:
.
Приклад:
,
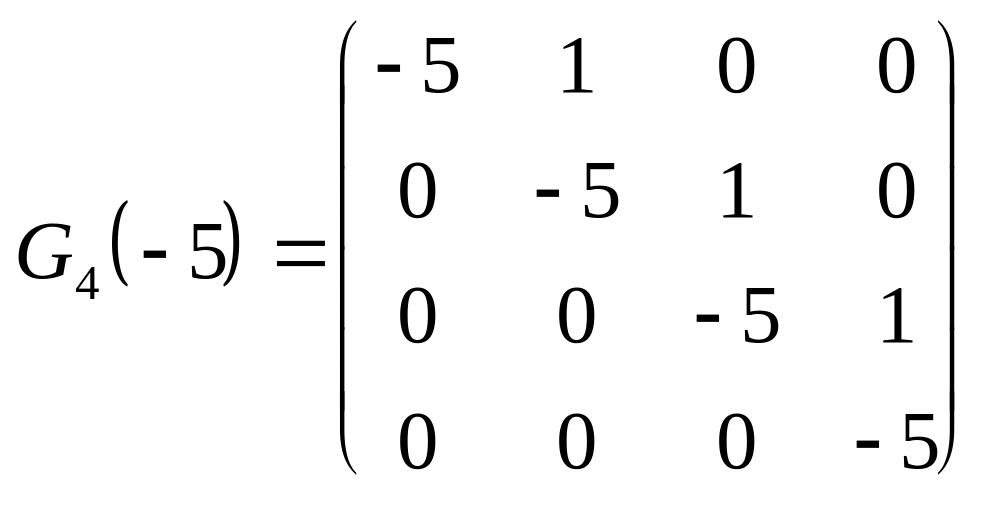Що
означає , що матр. має жорданову норм.
форму :
Тверження:
Дов. компл. кв. матр. А подібна матр.
, що має нормальну Жорданову форму.
Тобто
(
компл. матр.)
,
де B - має жорданову нормальну
форму.B-Жорд. норм. форма матр.А.
Твердження:
розміру n* n.
подібні коли вони мають одн. норм. Жорд.
форми(НЖФ).
Зауваження: 1) Матр. мають одн. НЖФ , якщо останні відр. розташ. жорд. клітин.
2)
Тв.про існ. жорд. нор.форми залиш. дійсним
для
,
якщо
-має
тільки дійсні корені.
Означення:
Базис
-наз.
жордан. базисом , якщо
в цьому базисі відпов. матрице
,
що має ЖНФ.
Теорема: Для довільного лін. перетв. існує жорданів базис.
5. Многочлени, їх звідність. Ділення многочленів. Корені многочленів. Теорема Вієта.
Многочленом
п-го
степеня від невідомого х
називається вираз вигляду:
Число п
називається
степенем многочленна. Два многочлени
є рівними, якщо рівними є їх коефіцієнти
при однакових степенях змінної. Число
0 теж є многочленом, степінь якого не
визначений. Роль 1 при діленні многочленів
відіграє число 1 як многочлен нульового
степеня. Многочлен f(x)
тоді
і тільки тоді має обернений, якщо він
є многочленом нульового степеня. Звідси
випливає, що оберненої операції до
множення многочленів – ділення- не
існує. Для многочленів існує алгоритм
ділення з остачею, який грунтується на
тому, що для будь-яких двох многочленів
f(x),
g(x)
можна знайти такі многочлени q(x),
r(x)
що
f(x)=g(x)q(x)+r(x),
при чому степінь r(x)
менше степеня g(x)
або
r(x)=0.
Многочлени g(x),
r(x)визначаються
однозначно. Властивості ділення
многочленів:
1.Якщо f(x) ділиться на g(x), а g(x)ділиться на h(x), то f(x) ділиться на h(x).
2.Якщо f(x) i g(x) діляться на h(x), то їх сума і різниця теж ділиться на h(x).
3.Якщо f(x) ділиться на g(x), то добуток f(x) на інший многочлен теж ділиться на g(x).
4.Якщо
кожен з многочленів
ділиться
на
g(x),
то
на
g(x)
буде
ділитися
многочлен
.
5,Всякий многочлен ділиться на будь-який многочлен нульового степеня.
6,Якщо f(x) ділиться на g(x), то він ділиться і на сg(x).
7.Многочлени cf(x) і тільки вони будуть дільниками f(x) , які мають такий же степінь, що й f(x).
8.Многочлени f(x) i g(x) тоді і тільки тоді діляться один на другий, коли f(x)=cg(x)
Якщо f(c)=0, то с називається коренем многочленна f(x)
Корені многочленів.
Озн 1.
Коренем многочлена
називається елемент
будь-якого
розширення
поля
такий,
що
.
Озн 2.
Коренем
називається елемент
,
якщо
.
Твердження.
Елемент
є
коренем многочлена
тоді
і тільки тоді, коли
ділиться
на
.
Доведення.
Згідно теореми Безу остача від ділення
на
дорівнює
.
Отже,
ділиться
на
тоді і тільки тоді, коли
,
тобто коли
- корінь многочлена
.
Озн 3.
елемент
називається
-кратним
коренем многочлена
,
якщо
ділиться на
,
але не ділиться на
.
Теорема
(Вієта).
Якщо
-
корені многочлена
,
то
,
,
.
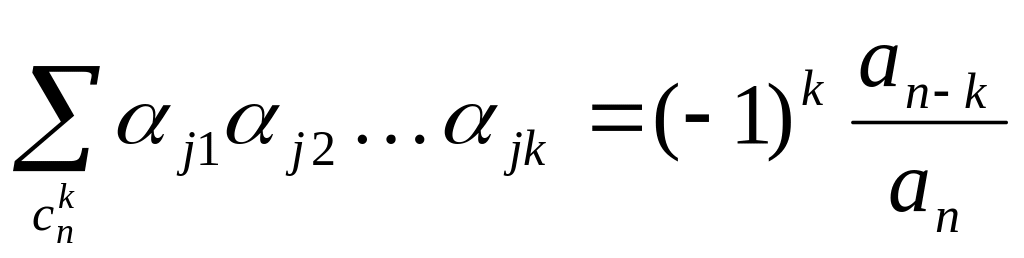Для
доведення цих формул треба виконати
множення у правій частині
,
звести подібні члени і прирівняти
коефіцієнти при однакових степенях
.