3. Расчет теплового воздействия струи двигателя, расширяющейся в вакуум, на плоскость.

Стандартная методика [5] достаточно простую чисто экспериментальную методику расчета тепловых потоков на плоскость, ориентированную произвольным образом к оси струи.

Рисунок 3.1- К расчету воздействия струи на плоскость

<0 X_max X

Y_max Y

h n

0 _мах ∆Х

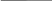
X_max ∆Y

Максимальные тепловые потоки на пластине реализуются в точке с координатой Х_max, вычисляемой по формуле:

Х_max = tg _max H (1)

Где при числах Маха на срезе сопла 3  М_а  5 с погрешностью 15%

tg _max = 0.57 (  (  -1))^0.5 М_а tg ( 45⁰ - /2 ) (2)

Зная величину Х_max и _max можно определить координаты точки максимума теплообмена на пластине в системе координат струи, где ось 0Х совпадает с осью струи с началом в центре выходного сечения сопла, а ось 0Y перпендикулярна 0Х. По этим координатам рассчитывается значения скоростного напора V² в точке максимального теплообмена. Именно скоростной напор является наиболее достоверной характеристикой неравновесной струи, расширяющейся в вакуум, и используется наряду с линейной скоростью V для пересчета всех необходимых ниже параметров.

Величины максимальных тепловых потоков на пластине q_Wmax рассчитываются по обобщенной зависимости числа Стантона St от параметра разреженности к². На графиках рисунка 3.2 представлены зависимости чисел Стантона от параметра разреженности на интервале значений параметра разреженности от 0.01 до 100. При значения параметра разреженности около 0.01 число Стантона близко к 1, что соответствует свободномолекулярному режиму обтекания, когда вся кинетическая энергия молекул переходит к телу.

Рисунок 3.2- К расчету воздействия струи на плоскость

Параметр разреженности;

к² =((-1)/2)( V R_хТ_х)/(Т₀_х) (3)

где Т_х – характерная температура, определяемая по формуле:

Т_х = ( Т_W + Т₀)/2 (4)

Тогда вязкость является функцией характерной температуры:

_х=_х(Т_х) (5)

Под R_х понимается половина размера торца, при  = 0 и  =1.4 определяемый по формуле:

R_{х тор} = 0.37 Н (6)

При отклонении оси струи на угол  эффективный радиус определяется по формуле:

2R_{х тор} = R_{х цил} = 0.75 Н /( 1+0.25) (7)

Тепловой поток при к²> 0.2 определяется по формуле

q = V St ( I₀ - I_W) (8)

причем угол падения линии тока _max в точке максимума теплового потока учитывается по соотношению:

St = St_=0 cos _max (9)

Следует отметить, что все формулы методики используют следующие весьма спорные в определении параметры двигателя:

-  - показатель адиабаты в струе;

• М_а – число Маха на срезе сопла;

• V - плотность тока в точке расчета;

• I₀ и I_W это энтальпия торможения в камере и энтальпия при температуре стенки.

Использование в формуле для теплового потока энтальпии торможения в камере неслучайно, ведь несмотря на то, что колебательная энергия запасена была молекулами в камере сгорания и в дальнейших процессах переноса в струе не участвует, при ударе молекулы о стенку молекула отдаст стенке всю свою энергию, в том числе и колебательную. А полная энтальпия и есть мера этой полной энергии молекул. Другое дело, что при расчете числа Стантона в газодинамических процессах принимают участие только поступательные и вращательные степени свободы молекул, и температура газа не является равновесной, а следовательно, возникают проблемы с определением чисел Маха. Как уже отмечалось раньше, показатель адиабаты в струе следует принять соответствующим замороженным колебательным степеням свободы, то есть равным 1.33 для типичной смеси продуктов сгорания двигателей на АТ и НДМГ. Основными компонентами этой смеси являются трехатомные молекулы СО₂, имеющие гантелеобразную структуру с пятью степенями свободы, и молекула воды Н₂О, имеющая треугольную пространственную структуру и шесть степеней свободы. Для того чтобы избежать ошибок при прямом определении чисел Маха в струе, можно использовать комплекс М_а², который часто встречается в формулах. И только там, где необходимо четко использовать именно число Маха, его определяют делением комплекса М_а² на 1.33- значение показателя адиабаты замороженного течения. Определить комплекс М_а² можно, используя наиболее достоверные характеристики двигателя:

• Р – тяга двигателя;

• S_а – площадь;

• Р_а – статическое давление вблизи среза сопла.

Р/ S_а = Р_а + Р_аМ_а² (10)

Все вышесказанные рекомендации относятся к течению в основной изоэнтропической невязкой части струи, в которой можно считать постоянной энтальпию торможения. Но в пристеночной зоне ( или пограничном слое ) в сверхзвуковой части сопла струя теряет часть энергии на теплообмен со стенкой сопла, а также часть своей скорости в силу трения. Параметры струи в так называемом невязком ядре струи можно определить, используя поля параметров невязкого газа, истекающего в вакуум.