3.4 Гиперболическое движение

(p=0,e>1)

Каноническое уравнение гиперболы в центральных прямоугольных координатах Oξ!η! представляется в виде

(1.68)

где a - действительная, а b - мнимая полуоси гиперболы. Полуфокусное расстояние c=ae связано с полуосями зависимостью

,откуда , (1.69)

а фокальный параметр выражается через действительную полуось и эксцентриситет формулой

. (1.70)

Движение тела M всегда происходит только по одной ветви гиперболы: ближайшей к фокусу, в котором расположено гравитирующее тело M0, в случае притяжения тел, и удаленной от фокуса в случае их отталкивания. Мы ограничимся рассмотрением только притяжения тел.

Параметрические уравнения гиперболы:

, (1.71)

где F - угол с вершиной в центре гиперболы, отсчитываемый от направления оси Oξ!. Угол F является аналогом эксцентрической аномалии, а величина H - его выражением через гиперболические функции

(1.72)

Знание величины аналога эксцентрической аномалии F дает возможность геометрического построения точки гиперболы M, (рис. 1.5). Связь между орбитальными фокальными координатами ξ, η и центральными координатами ξ!, η! имеет вид .(1.153) Аналогично эллиптическому движению можно получить два соотношения, связывающие переменные величины r, v и F:

(1.72)

Направление отсчета углов v с вершиной в фокусе гиперболы и F с вершиной в центре гиперболы взаимно противоположны, т.е. при v > 0 будет F < 0 и наоборот. Путем возведения в квадрат и последующего сложения из этих уравнений можно исключить истинную аномалию v и получить зависимость r от F:

. (1.73)

Исключение r из равенств (1.72) приводит к следующей зависимости между v и F:

(1.74)

Убедиться в справедливости такой зависимости можно путем вычисления тангенса половинного угла:

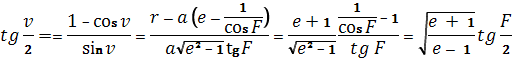(1.75)

Зависимость между аналогом эксцентрической аномалии и временем получим после вычисления интеграла J в (1.84). Для этого в интеграле J сделаем замену переменной v на F

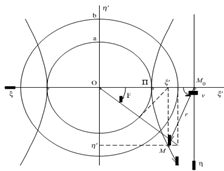
Рис. 1.5. Построение точки гиперболы M=(ξ!,η!)=(a/ cos F, b tg F ) по значению аналога эксцентрической аномалии F . Точка П - перицентр орбиты.

Учитывая

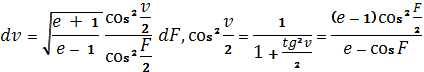(1.76)

для интеграла J получим

(1.77)

Проводя интегрирование и упрощение, представим результат в виде

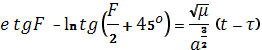(1.78)

Это уравнение своего имени не имеет. Его обычно называют аналогом уравнения Кеплера для гиперболического движения.

Если использовать гиперболические функции, то это уравнение принимает более простой вид. Действительно, если учесть, что

то уравнение запишется в виде

(1.79)

где , a - действительная полуось гиперболы.

Алгоритм вычисления координат и скоростей в гиперболическом движении на заданный момент времени t при известных кеплеровских элементах a,e,i,Ω,ω и M0 в эпоху t0

3.5 Параболическое движение

(p = 0, e = 1)

Уравнение параболической орбиты записывают в виде p r = 1 + cos v

(1.80)

где величина определяет расстояние от центра при тяжения M0 до вершины параболы. Величину q называют перицентрическим расстоянием для параболы. Ее обычно используют в качестве кеплеровского элемента вместо фокального параметра орбиты p.

Для вычисления интеграла

сделаем замену переменной интегрирования по формуле

(1.81)

Учитывая, что σ =0 при v = 0, а также

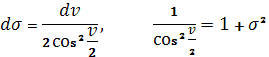(1.82)

получим:

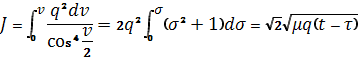(1.83)

Вычисление определенного интеграла приводит к уравнению Баркера:

(1.84)

где введено обозначение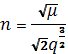

Определение величины σ из этого уравнения по заданному времени t обычно проводят численно, так как известная формула Кардано мало пригодна для вычислений.