Глава 2.Общее решение

Общее решение задачи двух тел можно получить из общего интеграла, представляющего собой не что иное, как неявную форму задания общего решения.

2.1 Общее решение в орбитальных координатах

В этом разделе рассматривается движение тела M в орбитальных прямоугольной M0ξηζ и цилиндрической M0rvζ системах координат. Положение орбитальной системы координат в пространстве определяется тремя кеплеровскими элементами Ω,i,ω. Долгота восходящего узла Ω и

наклонение i определяют положение плоскости орбиты M0ξη, а аргумент перицентра ω определяет положение оси M0ξ в плоскости орбиты. При переходе от относительной системы M0xyz к орбитальной системе M0ξηζ кеплеровские элементы Ω,i,ω считаются известными. Поэтому общее решение в орбитальной системе координат зависит только от трех оставшихся кеплеровских элементов p,e,τ, которые можно рассматривать как произвольные постоянные. Это отражено в последующей формуле, в которой фокальный параметр p, эксцентриситет e и время прохождения через перицентр τ входят в общее решение для орбитальной системы ξ, η, ξ˙, η˙, ζ=0, ζ˙=0, а элементы Ω,i,ω появляются только при переходе к относительной системе координат посредством направляющих косинусов ατ,βτ,γτ,α!,β’,γ‘.

Задача определения общего решения в орбитальных координатах сводится к получению зависимостей:

ξ, η, ξ˙, η˙

r, v, r˙, v˙

t, p, e.τ ,- для прямоугольной системы M0ξηζ ,

t, p, e, τ ,- для цилиндрической системы M0rvζ , (1.23)

а аппликата ζ и ее производная ζ˙ тождественно равны нулю.

Уравнение орбиты в полярных координатах связывает переменные r и v. Для вывода зависимости величин r и v от времени рассмотрим интеграл площадей в цилиндрической системе координат. Сначала при c1=c2=0 и c3=c с учетом ζ=ζ˙=0 запишем интеграл площадей в орбитальных декартовых координатах в виде

, (1.24)

а затем путем замены переменных

,

(1.25)

из (1.23) получим интеграл площадей в цилиндрической системе координат M0rvζ

, (1.26)

где r определяется формулой (1.8).

Интегрируя это равенство, получим зависимость времени t от истинной аномалии v в виде

(1.27)

где произвольная постоянная τ (момент прохождения через перицентр) соответствует значению истинной аномалии v=0. Это уравнение мы будем использовать в дальнейшем вместо интеграла , зависящего явно от времени.

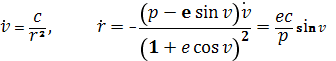(1.28)

Подставляя полученные значения для v˙ и r˙ в выражения (1.25) для ξ˙ и η˙ и учитывая, что зависимость t от v задается формулой (1.27), получим общее решение в орбитальной цилиндрической системе координат

(1.29)

С учетом (1.29) общее решение в орбитальных прямоугольных координатах будет задаваться формулами (1.25) после обращения интеграла (1.27), т.е. получения зависимости истинной аномалии v от времени t.

Радиальная и трансверсальная компоненты скорости движения тела M представляются в виде

(1.30)

а сама скорость записывается в виде:

(1.31)

2.2 Общее решение уравнений относительного движения

Рассмотрим на небесной сфере сферический треугольник N M x, где M - проекция текущего положения тела M на небесную сферу. Сторонами этого треугольника являются дуги больших кругов Q,xN=Ω, N M=u=ω+v– аргумент широты тела M , xQ,M = arccos(x/r). Угол при вершине N равен 180◦ − i. При v = 0 треугольник N M x преобразуется в треугольник N xξ, изображенный на рис. 1.3. По теореме косинусов сферической тригонометрии из треугольников N M x, N M y и N M z получим

x = rα = r(cos Ω cos u − sin Ω sin u cos i),

y = rβ = r(sin Ω cos u + cos Ω sin u cos i),

z = rγ = r sin u sin i. (1.32)

Направляющие косинусы α,β,γ радиус-вектора r относительно осей системы M0xyz здесь можно получить из (1.21) заменой аргумента перицентра ω на аргумент широты u.

Вычисляя путем дифференцирования по времени t компоненты скоростей, получим общее решение уравнений относительного движения в виде

,

,

, (1.33)

где

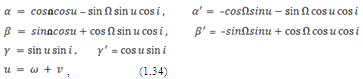
а штрих означает производную по аргументу широты:

.

К этим соотношениям следует добавить уравнения (1.29).

Общее решение можно вывести другим путем, используя решение в орбитальных координатах. В этом случае направляющие косинусы будут постоянными величинами, что удобно при вычислении координат и скоростей для большого числа моментов времени.

Используя формулы (1.13), общее решение в этом случае можно представить в виде

(1.35)

где величины ξ, η, ξ˙, η˙ определяют общее решение в орбитальной системе координат по формулам (1.25) и (1.29).