1.2 Орбитальная система координат

Орбитальная система координат вводится следующим образом. Ось направим по вектору Лапласа λ, ось - по вектору c, а ось - перпендикулярно к этим осям и так, чтобы система была правой. Плоскость ξη в орбитальной системе координат является плоскостью орбиты.

Орты орбитальной системы

,

,

(1.10)

полностью определяются компонентами векторов и :

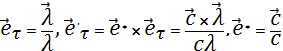. (1.11)

С помощью матрицы A направляющих косинусов осей орбитальной системы относительно системы

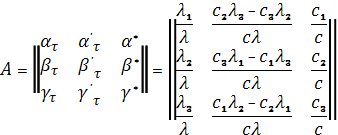(1.12)

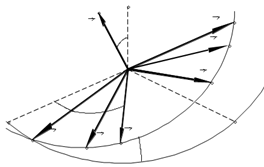
Рис. 1.2. Используемые ортонормированные базисы.

Можно выразить относительные координаты и скорости через орбитальные:

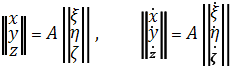(1.13)

Обратный переход осуществляется с помощью транспонированной матрицы AT , совпадающей с обратной матрицей A−1:

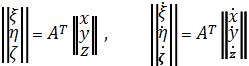. (1.14)

Все элементы матрицы A - постоянные величины.

В орбитальной системе координат векторы , , и имеют следующие компоненты:

= {λ, 0, 0}, ={0,0,c}, ={ ,η, }, = { , , }, (1.15)

Радиус-вектор и векторы скорости в радиальном r и трансверсальном направлении будем записывать в виде

, (1.16)

где e и e ! - единичные взаимно ортогональные векторы радиального и трансверсального направлений:

. (1.17)

Направляющие косинусы α,β,γ, являются переменными величинами. Верхний индекс (штрих) означает дифференцирование по угловой переменной u (или по v, учитывая, что u=v+ω и ω=const), зависящей от времени, что согласуется с правилом дифференцирования единичных векторов.

1.3 Кеплеровские элементы орбиты

Вместо произвольных постоянных c1,c2,c3,h,λ1,λ2,λ3,τ в астрономии обычно используются более наглядные и более удобные постоянные интегрирования, называемые кеплеровскими элементами орбиты: p,e,i,Ω,ω,τ.

Два первых кеплеровских элемента, p - фокальный параметр и e - эксцентриситет, определяют размер и форму орбиты. Элемент τ означает момент прохождения телом перицентра орбиты. Его называют еще ”динамическим моментом”, так как это единственный кеплеровский элемент, характеризующий динамику движения по орбите, в отличие от остальных элементов, имеющих геометрический характер.

Все углы будем также изображать дугами на небесной сфере. Прямая, по которой плоскость орбиты пересекается с основной координатной плоскостью M0xy, называется линией узлов, а точки ее пересечение с небесной сферой – узлами орбиты. Узел, при прохождении которого тело перемещается из полупространства z<0 в полупространство z>0, называется восходящим узлом орбиты, а противоположный узел - нисходящим узлом.

Три угловых элемента Ω, i и ω определяют положение орбиты в пространстве. Угол Ω в астрономии называется долготой восходящего узла. Он отсчитывается в плоскости M0xy от положительного направления оси абсцисс M0x до направления на восходящий узел орбиты. Диапазон изменения угла: 0≤Ω<2π. Угол i называется наклонением орбиты или наклоном. Это - двугранный угол между плоскостью M0xy и плоскостью орбиты, изменяющийся в диапазоне 0 ≤ i ≤ π.

Угол ω между линией узлов и линией апсид называется угловым расстоянием перицентра от узла или аргументом широты перицентра орбиты. Он измеряется в плоскости орбиты от восходящего узла до направления на перицентр орбиты, 0 ≤ ω < 2π.

Углы Ω,i и ω - это фактически хорошо известные из теоретической механики эйлеровы углы, прецессии, нутации и собственного вращения, определяющие ориентацию орбитальной системы координат M0ξηζ относительно осей системы M0xyz.

В астрономии углом прецессии служит долгота восходящего узла орбиты Ω, углом нутации - наклонение орбиты i, а углом собственного вращения - аргумент перицентра ω. Углы i и Ω определяют положение плоскости орбиты в пространстве, а угол ω-ориентацию орбиты в этой плоскости.

Соотношения между произвольными постоянными интегрирования и кеплеровскими элементами Ω,ω,i можно получить по формулам сферической тригонометрии из соответствующих сферических треугольников на небесной сфере. Вершины этих треугольников будем обозначать теми же буквами, что и соответствующие оси. Например, вершинами треугольника N xζ являются точки небесной сферы, полученные ее пересечением с положительным направлением осей Ox и Oζ , а также с направлением на восходящий узел орбиты O→N. Аналогично строятся другие треугольники, причем вершины соединяются дугами больших кругов.

Рассмотрим сначала упомянутый треугольник N xζ . Угол при вершине N у этого треугольника равен 90◦ − i. Сторона (дуга) N ζ равна 90◦, сторона xN равна Ω, а сторона xζ есть arccos(c1/c). По теореме косинусов тогда получим

. (1.18)

Аналогично, используя теорему косинусов, можно получить две формулы из треугольников N yζ и N zζ в виде

. (1.19)

Рассмотрим теперь треугольник N xξ (см. рис. 1.3). Он характеризуется углом 180◦ − i при вершине N и сторонами

и

.

По теореме косинусов из этого треугольника получим

(1.20)

Аналогичные формулы можно вывести из треугольников

N yξ и N zξ.

Рис. 1.3. Сферический треугольник N xξ.

Вся совокупность формул, определяющих постоянные интегрирования через кеплеровские элементы, такова:

(1.21)

Последнее равенство в (1.21) означает, что постоянная интегрирования τ совпадает с моментом прохождения через перицентр.

С помощью формул (1.21) можно осуществить обратный переход от постоянных интегрирования c, λ, h, τ к кеплеровским элементам p,e,i,Ω,ω,τ. Для этого сначала вычисляются p и e по формулам (1.8). Затем из равенства c3/c=cosi однозначно определяется наклонение i. Далее по двум направляющим косинусам c1/c и c2/c однозначно (с указанием четверти) определяется долгота восходящего узла Ω. А по двум направляющим косинусам вектора λ также однозначно определяется аргумент перицентра ω.

Уравнения (1.21) определяют выражения для направляющих косинусов осей Oξ и Oζ через угловые кеплеровские элементы орбиты Ω, i, ω. Аналогичные выражения для направляющих косинусов оси Oη имеют вид

(1.22)