
- •Заняття 15 Модуль 5. Функції багатьох змінних
- •§5.1. Поняття функції багатьох змінних. Область її визначення. Графік та лінії рівнів.
- •§ 5.2. Границя та неперервність функції багатьох змінних.
- •Дослідити послідовність на збіжність:
- •Дослідити чи існує границя функції в точці :
- •Дослідити функцію на неперервність:
- •§ 5.3. Частинні похідні. Повний диференціал. Диференційовність функції двох змінних. Похідна за напрямом. Градієнт.
- •Заняття 16
- •§ 5.4. Екстремум функції двох змінних. Найбільше та найменше значення функції двох змінних в замкненій області
- •1. Дослідити на екстремум функції:
- •Знайти найбільше та найменше значення функції в замкненій області , якщо:
§ 5.2. Границя та неперервність функції багатьох змінних.
Точку
![]() називають границею
послідовності точок
називають границею
послідовності точок
![]() ,
якщо
,
якщо
![]() .
(2)
.
(2)
Для
того, щоб послідовність
![]() збігалася до точки
збігалася до точки
![]() ,
необхідно і достатньо, щоб
,
необхідно і достатньо, щоб
![]() .
.
Число
називають границею
функції
![]() в точці
в точці
![]() ,
якщо для довільної послідовності точок
,
якщо для довільної послідовності точок
![]() ,
збіжної до
,
виконується рівність
,
збіжної до
,
виконується рівність
![]() .
.
У
цьому випадку пишуть:
![]() .
.
Надалі
у цьому розділі в основному розглядаються
функції
двох змінних і замість послідовності
![]() будемо писати
будемо писати
![]() .
.
Функцію
називають неперервною
в точці
![]() ,
якщо для довільної послідовності точок
,
якщо для довільної послідовності точок
![]() ,
збіжної до
,
збіжної до
![]() ,
має місце рівність
,
має місце рівність
![]() .
.
Функцію, яка неперервна у всіх точках деякої області, називають неперервною у цій області. Графіком такої функції є деяка поверхня.
Приклади.
Дослідити послідовність на збіжність:
а)
![]() ;
;
б)
![]()
Розв’язання:
а)
Оскільки
![]() ;
;
![]() ;
;
![]() ,
то
,
то
![]() .
.
б)
Оскільки послідовність
![]() не має границі, то і вся послідовність
границі не має.
не має границі, то і вся послідовність
границі не має.
Дослідити чи існує границя функції в точці :
а)
![]() ,
,
![]() ;
;
б)
![]() ,
,
![]() .
.
Розв’язання.
а)
Оскільки
![]() і
і
![]() ,
то
,
то
![]() .
.
б)
Доведемо, що функція
![]() не має границі в точці
.
Для цього розглянемо дві послідовності
не має границі в точці
.
Для цього розглянемо дві послідовності
![]() і
і
![]() ,
які збігаються до точки
,
але послідовності
,
які збігаються до точки
,
але послідовності
![]() та
та
![]() мають різні границі.
мають різні границі.
Нехай
![]() .
Тоді
.
Тоді

Нехай
![]() .
Тоді
.
Тоді

Оскільки
![]() ,
але
,
але
![]() ,
то дана функція не має границі в точці
.
,
то дана функція не має границі в точці
.
Дослідити функцію на неперервність:
а)
![]() ;
;
б)
![]() ;
;
Розв’язання.
а)
Оскільки функції
![]() та
неперервні на всій площині, то функція
є неперервною у всіх точках площини за
виключенням тих точок, де
та
неперервні на всій площині, то функція
є неперервною у всіх точках площини за
виключенням тих точок, де
![]() .
У точці
функція не визначена. Більше того,
функція
не має границі в точці
.
Справді, якщо
,
то
.
У точці
функція не визначена. Більше того,
функція
не має границі в точці
.
Справді, якщо
,
то
![]() і
і
![]() .
.
Якщо
![]() ,
то
,
то
![]() ,
але
,
але
![]() .
.
б)
Функція
неперервна на всій області свого
визначення, тобто у всіх точках
![]() площини, для яких
площини, для яких
![]() .
.
Точки
площини, для яких виконується умова
![]() є точками розриву. Множина точок розриву
складається з двох прямих:
є точками розриву. Множина точок розриву
складається з двох прямих:
![]() та
та
![]() .
.
Завдання для самостійного розв’язування.
Знайти границі (якщо вони існують) наступних послідовностей:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() .
.
Знайти границю (якщо вона існує) функції в точці:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
;
Дослідити функцію на неперервність та охарактеризувати множину точок розриву:
1)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]()
§ 5.3. Частинні похідні. Повний диференціал. Диференційовність функції двох змінних. Похідна за напрямом. Градієнт.
Н ехай
функція
визначена у деякому околі точки
ехай
функція
визначена у деякому околі точки
![]() .
Розглянемо все можливі прирости для
цієї точки.
Приріст
можна задати лише по змінній
і дістанемо точку
.
Розглянемо все можливі прирости для
цієї точки.
Приріст
можна задати лише по змінній
і дістанемо точку
![]() .
Якщо надати приріст лише по змінній
.
Якщо надати приріст лише по змінній
![]() ,
то дістанемо точку
,
то дістанемо точку
![]() .
.
![]()
якщо ця границя існує, то її називають частинною похідною функції по змінній х і символічно позначають одним з наступних способів:
![]() або
або
![]() або
або
![]() .
.
Аналогічно означається частинна похідна функції по змінній у:
![]() .
.
При
знаходженні частинної похідної по
змінній х
від функції
змінна у
залишається постійною. Тому функція
при цьому може трактуватися як функція
від однієї змінної х:
![]() ,
а змінну y
можна сприймати як деякий параметр.
Тоді частинна похідна від функції
по змінній х
є звичайною похідною від функції
.
Аналогічно, обчислюючи частинну похідну
по змінній у,
змінну х
потрібно вважати постійною.
,
а змінну y
можна сприймати як деякий параметр.
Тоді частинна похідна від функції
по змінній х
є звичайною похідною від функції
.
Аналогічно, обчислюючи частинну похідну
по змінній у,
змінну х
потрібно вважати постійною.
Частинні
похідні
![]() та
та
![]() теж є функціями двох змінних. Частинні
похідні (якщо вони, звичайно, існують)
від функцій
та
називають частинними похідними другого
порядку. За означенням:
теж є функціями двох змінних. Частинні
похідні (якщо вони, звичайно, існують)
від функцій
та
називають частинними похідними другого
порядку. За означенням:
![]()
![]() .
.
Похідні
![]() та
та
![]() називають мішаними
похідними другого порядку.
У випадку неперервності мішаних похідних,
вони рівні між собою (
=
).
називають мішаними
похідними другого порядку.
У випадку неперервності мішаних похідних,
вони рівні між собою (
=
).
Аналогічно означаються частинні похідні вищих порядків.
Диференціалом
функції
![]() називається сума добутків частинних
похідних цієї функції на прирости
відповідних незалежних змінних.
називається сума добутків частинних
похідних цієї функції на прирости
відповідних незалежних змінних.
![]() .
.
Оскільки
![]() ,
,
![]() ,
то
,
то
![]() .
.
Функцію
називають диференційовною
в точці
![]() ,
якщо її повний приріст у цій точці може
бути представлений у вигляді :
,
якщо її повний приріст у цій точці може
бути представлений у вигляді :
![]() ,
,
де
![]() ,
,![]() і
і
![]() при
при
![]() .
.
Як і для функцій
однієї змінної з диференційовності
функції
в деякій точці слідує неперервність
цієї функції у цій точці. Для функції
однієї змінної
![]() існування скінченної похідної
існування скінченної похідної
![]() було необхідною і достатньою умовою
диференційовності цієї функції. Для
функції двох змінних ситуація значно
складніша. З існування скінченних
частинних похідних
та
було необхідною і достатньою умовою
диференційовності цієї функції. Для
функції двох змінних ситуація значно
складніша. З існування скінченних
частинних похідних
та
![]() не слідує навіть неперервність функції
і тому існування скінченних частинних
похідних ще недостатньо для диференційовності
функції двох зміннних. Проте, якщо
функція
в деякому околі точки
не слідує навіть неперервність функції
і тому існування скінченних частинних
похідних ще недостатньо для диференційовності
функції двох зміннних. Проте, якщо
функція
в деякому околі точки
![]() має неперервні
частинні похідні
має неперервні
частинні похідні
![]() і
і
![]() ,
то функція
диференційовна в точці
,
то функція
диференційовна в точці
![]() .
.
Якщо
функція
диференційовна в точці
,
то для досить малих
![]() і
і
![]() правильна наближена рівність
правильна наближена рівність
![]()
Нехай
функція
визначена в околі точки
,
![]() – деякий вектор, який утворює кут
– деякий вектор, який утворює кут
![]() з додатним напрямом осі
.
з додатним напрямом осі
.
Похідною
![]() у напрямку, що визначається вектором
називають границю (якщо вона існує)
у напрямку, що визначається вектором
називають границю (якщо вона існує)
![]() .
.
Можна довести, що
![]() .
.
Похідна характеризує швидкість зміни функції у напрямку вектора , який утворює кут з додатним напрямом осі Ох.
Градієнтом
функції
називають вектор з координатами
![]()
![]()
![]() .
.
Градієнт
![]() функції
в точці
функції
в точці
![]() вказує напрям найшвидшої зміни функції
у цій точці.
вказує напрям найшвидшої зміни функції
у цій точці.
Приклади.
Знайти частинні похідні першого порядку:
а)
![]() ;
;
б)
![]() .
.
Розв’язання.
а) Вважаючи постійною, отримаємо:
![]()
![]() .
.
Вважаючи
![]() постійною, отримаємо:
постійною, отримаємо:
![]()
![]() .
.
б)
![]() .
.
![]() .
.
Знайти частинні похідні першого та другого порядків функції
 .
Обчислити
.
Обчислити
 ,
,
 .
.
Розв’язання.
![]() ,
,
![]() .
.
![]() ,
, ![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
Знайти повний диференціал функції
 .
.
Розв’язання. Повний диференціал може бути записаний у вигляді
![]() .
.
Оскільки
![]() і
і
![]() ,
то
,
то
![]() .
.
Обчислити наближено
 ,
замінюючи повний приріст функції її
повним диференціалом.
,
замінюючи повний приріст функції її
повним диференціалом.
Розв’язання.
Розглянемо
функцію
![]() .
Ця функція є диференційовною в околі
точки
.
Ця функція є диференційовною в околі
точки
![]() ,
причому
,
причому
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Тому
.
Тому
![]() ,
,
де
![]() .
.
![]() .
.
Знайти градієнт функції
 в точці
в точці
 .
.
Розв’язання.
![]() .
.
![]() .
.
![]() ,
, ![]() .
.
Отже,
![]() .
.
Вказати точки, в яких градієнт функції
![]() співпадає
з вектором
співпадає
з вектором
![]() .
.
Розв’язання.
![]() .
.
![]() тоді
і тільки тоді, коли
тоді
і тільки тоді, коли
![]()
![]()
Отже,
існує чотири точки, в яких градієнт
функції
співпадає з вектором
![]() .
Це точки
.
Це точки
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Знайти похідну функції
 в точці
в точці
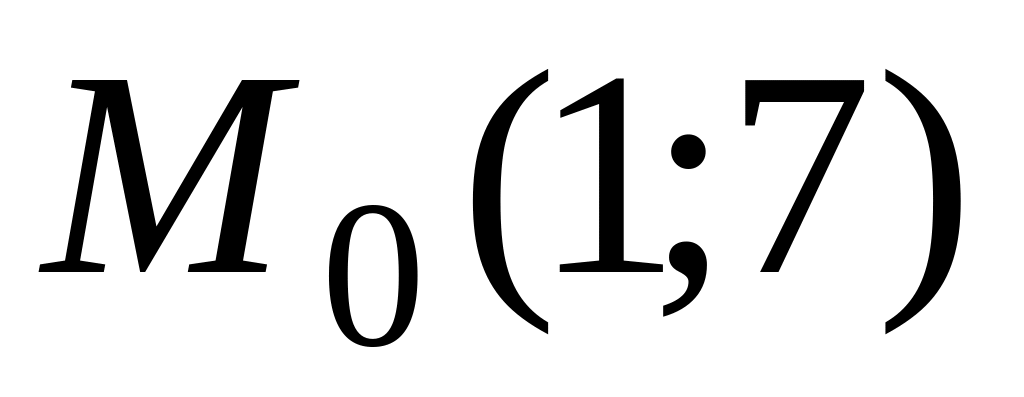 у напрямі вектора
у напрямі вектора
 .
.
Розв’язання. Знайдемо орт вектора
![]() .
.
Отже,
вектор
утворює з додатним напрямом осі
кут
такий, що
![]() ,
,
![]() .
.
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
Отже,
![]() .
.
Завдання для самостійного розв’язування.
Знайти частинні похідні першого порядку наступних функцій:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() ;
;
5)
![]() ;
6)
;
6)
![]() ;
7)
;
7)
![]() ;
;
Знайти значення частинних похідних
 в точці
в точці
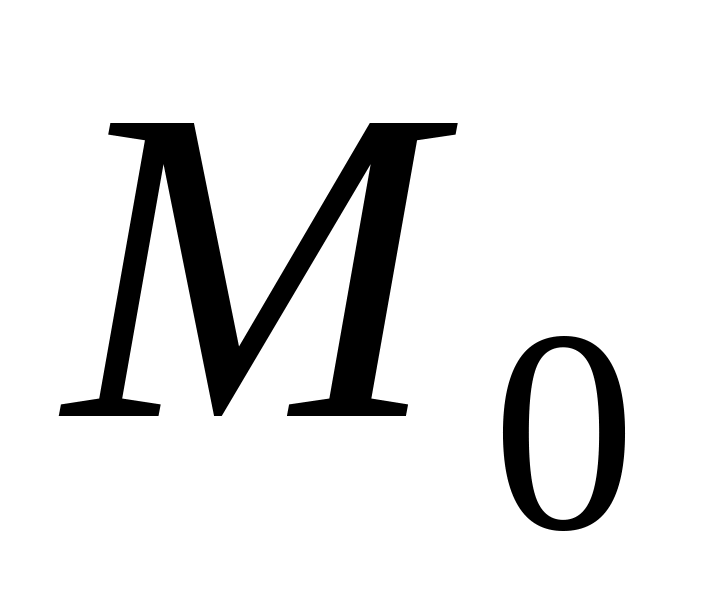 .
.
1)
![]() ,
,
![]() ;
2)
;
2)
![]() ,
,
![]() ;
;
3)
![]() ,
,
![]() .
.
Знайти повний диференціал функції:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
;
4)
![]() ;
5)
;
5)
![]() ;
;
Замінюючи повний приріст функції її повним диференціалом, обчислити наближене значення наступних виразів:
1)
а)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() .
.
Знайти градієнт функції в точці :
1)
![]() ,
,
![]() ;
2)
;
2)
![]() ,
,
![]() .
.
Вказати точки, в яких градієнт функції збігається з вектором .
1)
![]() ,
,
![]() ;
2)
;
2)
![]() ,
,
![]() .
.
Знайти похідну функції в точці у напрямі вектора .
1)
![]() ,
,
![]() ,
,
![]() ;
2)
;
2)
![]() ,
,
![]() ,
,
![]() ;
;
3)
![]() ,
,
![]() ,
,
![]() ;
4)
;
4)
![]() ,
,
![]() ,
,
![]() .
.
