Властивості, пов’язані з парністю і непарністю функцій

1. Алгебраїчна сума скінченої кількості парних (непарних) функцій є функція парна (непарна).

2. Добуток скінченої кількості парних функцій є функція парна.

3. Добуток скінченої кількості непарних функцій є функція парна, якщо кількість множників є число парне, і є функція непарна, якщо кількість множників – число непарне.

4. Сума парної і непарної функцій, кожна з яких відмінна від функції , є функція, яка не належить ні до парних, ні до непарних.

5. Добуток парної і непарної функцій є функція непарна.

6. Якщо і – функції однакової (різної) парності і 0 для всіх хD(g), то функція є парною (непарною).

7. Складена функція є парною, якщо внутрішня функція парна або якщо внутрішня функція непарна, а зовнішня парна. Якщо внутрішня та зовнішня функції є непарними, то складена функція є непарною.

Монотонні функції. Функцію y=f(x) називають: а) зростаючою; б) спадною; в) незростаючою; г) неспадною, якщо для всіх x₁, x₂D(f) таких, що відповідно справедливі нерівності: а) ; б) ; в)  ; г) (рис. 3.2). Функцію y=f(x) називають монотонною, якщо вона є незростаючою або неспадною, і строго монотонною, якщо вона є зростаючою або спадною.

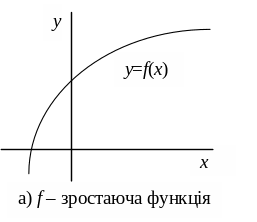
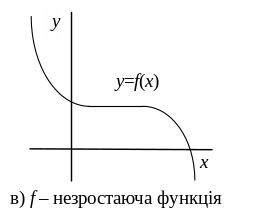
Рис. 3.2

Періодичні функції. Функцію y=f(x) називають періодичною, якщо існує число Т0 таке, що для будь-якого хD(f) виконуються умови: 1) х+ТD(f); 2) . При цьому число Т називають періодом функції y=f(x).

Якщо Т – період функції y=f(x), то число nT (nN) також є періодом цієї функції, а якщо, крім того, х–ТD(f) для будь-якого хD(f), то число nT (nZ, n0) також є періодом функції f. Отже, якщо функція періодична, то вона має безліч періодів. Найменше додатне число, що є періодом функції y=f(x), називають основним періодом цієї функції.

На рис.3.3. зображено графік періодичної функції з основним періодом Т.

Не кожна періодична функція має основний період. Наприклад, функція f(x)=с, де с – деяке дійсне число, періодична, бо для будь-якого хD(f) виконується рівність =с, причому при будь-якому ТR. Отже, кожне дійсне число, відмінне від нуля, є періодом цієї функції. Проте найменшого серед таких чисел не має. Отже, ця періодична функція основного періоду не має.

Для функцій , основний період дорівнює 2, а для функцій і – дорівнює .

Якщо функція y=f(x) періодична і має період Т, то функція (А, k, b – сталі, А0, b0) також періодична, причому її період дорівнює . Зокрема, якщо Т – основний період функції y=f(x) і k>0, то – основний період функції . Так, наприклад, функції , , мають основні періоди, що дорівнюють , , відповідно.

Обмежені функції. Функцію y=f(x) називають обмеженою зверху (обмеженою знизу), якщо існує таке число М (m),що для будь-якого хD(f) виконується нерівність f(x)≤M (f(x)≥m) (рис.3.4 (а, б)). Функцію y=f(x) називають обмеженою, якщо вона обмежена зверху і знизу, тобто, якщо існує таке число М>0, що для будь-якого хD(f) виконується нерівність (рис.3.4 (в)).

Рис.3.4

Функції:

1) стала y=с, с=const;

2) степенева , де  – фіксоване число;

3) показникова , а>0, а1, де а – фіксоване число;

4) логарифмічна , а>0, а1, де а – фіксоване число;

5) тригонометричні: , , , ;

6) обернені тригонометричні: , , , називають основними елементарними функціями.

Області визначення основних елементарних функцій є такими:

1. D(с)=R.

2. якщо =nN , то ;

якщо =–n, nN , то ;

якщо – нескоротний дріб, mZ, nN, то

=R, коли m>0 і n=2k+1;

=R\{0}, коли m<0 і n=2k+1;

=[0;+), коли m>0 і n=2k;

=(0;+), коли m<0 і n=2k;

якщо  – ірраціональне число, то

=[0;+), коли >0;

=(0;+), коли <0.

3) .

4) .

5) , ,

, .

6) , , , .

Графіки основних елементарних функцій зображено на малюнках 3.5-3.19

Рис. 3.6.

Рис. 3.7.

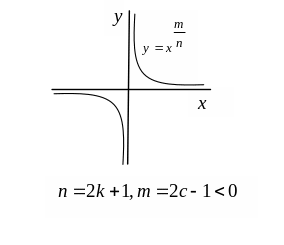
Рис. 3.8.

Рис. 3.9.

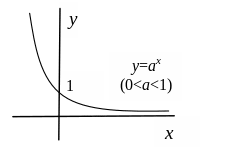
Рис.3.10

Рис.3.11

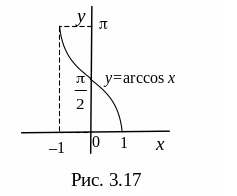
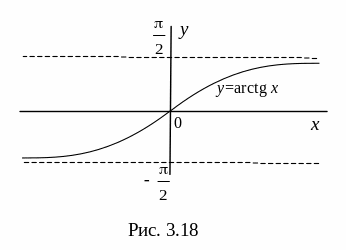
З основних елементарних функцій за допомогою арифметичних операцій та операції суперпозиції функцій можна утворювати нові функції. При цьому, якщо кількість таких операцій скінченна, то утворену функцію називають елементарною. Наприклад, , – елементарні функції.

Елементарні функції поділяють на такі класи.

1. Цілі раціональні функції. Це функції вигляду

,

де n – натуральне число або 0, – фіксовані числа. Цілі раціональні функції також називають многочленами, а числа – коефіцієнтами цих многочленів. Якщо , то число n називають степенем заданого многочлена.

2. Дробово-раціональні функції. Це функції вигляду

,

де і – многочлени, причому і степінь n многочлена відмінний від нуля.

Цілі і дробово-раціональні функції називають раціональними функціями.

3. Ірраціональні функції. Це функції, які утворені за допомогою суперпозиції раціональних функцій, степеневих функцій з раціональними показниками і чотирьох арифметичних операцій, застосованих скінченну кількість разів. Наприклад, – ірраціональна функція.

4. Алгебраїчні функції. Це функції y=y(x), що є розв’язками рівняння

,

де – многочлени від х.

Кожна раціональна і ірраціональна функції є алгебраїчною функцією.

5. Трансцендентні функції. Це функції, які не є алгебраїчними.

Можна показати, що тригонометричні, обернені тригонометричні, показникова і логарифмічна функції є трансцендентними функціями.