Вступ

Сонячні елементи – це напівпровідникові фотоелектричні пристрої, які призначені для перетворення сонячної енергії в електричну. Їх ще називають фотоперетворювачами. Вони входять у великий клас напівпровідникових приладів, які називають фотоелементами. Основними показниками якості сонячних елементів є коефіцієнт перетворення світлової енергії в електричну, термічна стабільність, радіаційна стійкість.

Найчастіше сонячний елемент являє собою твердотільну конструкцію із напівпровідникових матеріалів, які добре поглинають світло, а також металевих та діелектричних шарів. В основі функціонування сонячного елементу лежить явище вентильного фотоефекту. Поглинуті напівпровідником світлові кванти звільнюють електрони і дірки від внутрішніх кристалічних зв’язків і переводять їх в рухомий стан. Після, протилежно заряджені вільні носії заряду просторово розділяються переміщуючись в протилежних напрямках за рахунок дифузії, або дрейфу в силововому полі. Це силове поле повинно існувати в напівпровіднику. Такі ділянки в напівпровіднику, де на вільні носії діє сила струму називаються бар’єрами.

Механізм розділення носіїв відіграє роль своєрідного вентиля, який протидіє безпосередній взаємодії збуджених світлом вільних електронів і дірок. Щоб прорекомбінувати, вони повинні пройти по зовнішньому колу, де їх надлишкова потенціальна енергія, яка отримана внаслідок поглинання світла, перетворюється в кінетичну енергію рухомого заряду (електричний струм).

Незважаючи на те, що механізм вентильного фотоефекту відомий з 1839 р. і був відкритий Бекерелем, початком його практичного застосування можна вважати п’ятидесяті роки 20 ст., коли були створені батареї сонячних елементів для забезпечення енергією штучних супутників Землі і космічних лабораторій. Вважається, що практичне використання в енергетиці можуть знаходити лише фотоперетворювачі з ККД > 10%. Зараз створені сонячні елементи з ККД > 25%.

Основним матеріалом для сонячних батарей в даний час є кремній. Ефективність сонячних елементів на основі кремнію складає 15 ÷ 16% при прямому опромінюванні в умовах навколоземного космосу. У наземних умовах ккд кремнієвих елементів складає близько 20% при прямому сонячному опромінюванні і до 25 ÷ 27% при (30 ÷ 50) - кратній концентрації сонячного випромінювання. Основним недоліком кремнієвих елементів є значне зменшення ккд при збільшенні робочої температури.

Великі значення ккд і високу радіаційну стійкість мають сонячні елементи на основі гетероструктур. На даний час у світі освоєний випуск гетероперехідних елементів з кількома p-n-переходами (каскадні сонячні елементи), ккд яких наближається до 40%. Такі сонячні елементи створені на основі GaAs, який належить до сполук А ³В ⁵.

Розділ 2. Характеристика електричних процесів на контакті метал- напівпровідник

Явища на контакті метал напівпровідник

Розглянемо контакт напівпровідника n-типу з металом. Їх розділяє тонкий вакуумний шар. Робота виходу з напівпровідника менша ніж робота виходу з металу W_HП < W_M.

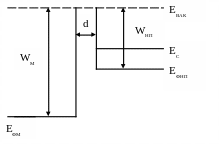
Рис. 1. Діаграма енергетичних зон металу і напівпровідника у початковий момент

зближення.

Якщо метал і напівпровідник привести в електричний контакт, то між ними буде відбуватися обмін електронами. Електрони, які виходять з металу внаслідок термоелектронної емісії потрапляють в напівпровідник, а електрони які виходять з напівпровідника потрапляють в метал внаслідок тієї ж причини. Однак оскільки термодинамічна робота виходу електронів з металу більша ніж з напівпровідника, то густина потоку електронів із металу в напівпровідник буде менша j_М < j_НП.

В результаті цього буде відбуватися перенесення електронів із напівпровідника в метал і метал буде заряджатися від'ємно, а напівпровідник додатньо. Такий перехід електронів із напівпровідника в метал буде відбуватися до того часу, поки рівні Фермі в металі і напівпровіднику не вирівняються, тобто встановиться стан термодинамічної рівноваги. Між металом і напівпровідником виникне електричне поле і контактна різниця потенціалів φ_К.

φ_К = (W_М - W_НП) / e. (1)

Р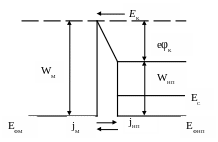 ис. 2. Енергетична діаграма структури метал-напівпровідник у стані термодинамічної рівноваги.

Електрони, які виходять з напівпровідника, щоб потрапити в метал, мають подолати додатковий потенціальний бар'єр величиною eφ_К. Відповідно робота виходу електронів з напівпровідника в метал збільшиться на величину eφ_К, а потік електронів з напівпровідника зменшиться і в стані термодинамічної рівноваги густини струмів з металу в напівпровідник і з напівпровідника в метал зрівноважаться. В реальному випадку величина φК може змінюватися від 0,1 до 1,5В і не перевищує ширини забороненої зони напівпровідника.

У приповерхневому шарі напівпровідника товщиною d_n залишається нерухомий об'ємний заряд додатньо іонізованих донорів і цей шар буде збіднений на основні носії заряду, тобто цей шар буде являтися діелектриком. Через малі розміри вакуумної щілини в подальшому ми її розглядати не будемо. Оскільки опір приповерхневого шару напівпровідника товщиною d_n буде великим порівняно з об'ємом напівпровідника, то цей шар називають запірним або областю просторового заряду.

Вигин зон Виникнення запірного шару, де створюється додатній нерухомий об'ємний заряд, приводить до вигину зон у цьому шарі, еквівалентному виникненню контактної різниці потенціалів. Максимальне

значення вигину зон рівне величині eφ_k, а хід зон в цьому шарі являє собою

хід потенціальної енергії електрона.

Поскільки ширина забороненої зони в області контакту метал-напівпровідник не змінюється, то стеля валентної зони зміщується еквівалентно до зміщення дна зони провідності. Ширина забороненої зони залишається постійною. В даному випадку зони вигинаються вверх. Основні носії заряду, в даному випадку електрони, будуть скочуватися в об'єм напівпровідника. А дірки, які є неосновними носіями заряду будуть підходити з об'єму напівпровідника до поверхневого шару.

Error: Reference source not found

Е_К

Рис. 3 Енергетична діаграма випрямляючого контакту метал-напівпровідник у стані

термодинамічної рівноваги.

При протилежному співвідношенні термодинамічних робіт виходу W_HП > W_M в напівпровіднику n-типу провідності виникає збагачений електронами приповерхневий шар. Тобто виникає область напівпровідника збагачена основними носіями заряду, опір якої значно нижчий ніж в об'ємній частині напівпровідника. Така система не являється випрямляючою і зони в напівпровіднику тепер будуть вигинатися вниз. Такий контакт називається антизапірним і його використовують для отримання омічних контактів металу з напівпровідником. Енергетична діаграма системи метал-напівпровідник у цьому випадку буде мати такий вигляд:

Рис. 4 Енергетична діаграма контакту метал-напівпровідник n-типу провідності у випадку утворення анти запірного шару.

В даному випадку електрони із об'єму напівпровідника скочуються в область просторового заряду, дірки ж навпаки з приповерхневого шару рухаються в об'єм напівпровідника. Аналогічні процеси будуть відбуватися в області контакту металу з напівпровідником р-типу провідності. Однак, оскільки в напівпровіднику р-типу основними носіями є дірки, то при співвідношеннях W_HП >W_M, в напівпровіднику р-типу буде виникати запірний шар і такий контакт буде випрямляючим. Якщо W_HП < W_M, то для р-типу провідності буде виникати антизапірний шар і ефекту випрямлення спостерігатися не буде.

2.4. Залежність напруженості поля і електростатичного потенціалу від віддалі в запірному шарі і від концентрації електронів в об`ємі напівпровідника

Внаслідок збіднення запірного шару основними носіями заряду зростає його опір, так що вся контактна різниця потенціалів розподіляється в цьому шарі. Крім того, як правило вважають, що всязовнішня різниця потенціалів також падає на тому ж шарі і сумарна зміна потенціалів (вигин зон) спостерігається лише в області запірного шару.

Розглянемо знову контакт напівпровідника n-типу з металом при умові Ф_н/п<Ф_м.

В цьому випадку в напівпровіднику виникає запірний шар рис.2.4 Концентрація вільних електронів в шарі визначається у вигляді

n=Nс e ^- (2.22)

Де e - потенціальна енергія електрона, що відповідає вигину дна зони провідності. Тут приймається , що величини e і мають абсолютні значення, тобто e >0.

Концентрація електронів в об`ємі напівпровідника

n₀=Nс e ^- . (2.23)

Візьмемо на внутрішній границі запірного шару n=n₀ і =0, так що відлік в даному випадку ведемо від E_co

Відповідно, маємо

n=n₀ e ^- . (2.24)

Припустимо, що n₀= N_d= N_d⁺, тобто всі донори іонізовані.

Тоді густина об`ємного заряду в запірному шарі буде рівна

=eN_d⁺- en= en₀(1-e^- ). (2.25)

Якщо зони викривлені помітним чином, так що e >>kT, то другим додатком в (4) можна знехтувати і вважати, що

= en₀= eN_d⁺ , (2.26)

тобто вважати постійним у всьому шарі. Густина об`ємного заряду і потенціал зв`язані рівнянням Пуасона:

=- =- . (2.27)

Інтегруючи це рівняння будемо мати:

(2.28)

Поскільки при , тобто на внутрішній границі шару , то .

Відповідно

(2.29)

тобто напруженість поля є лінійною функцією x .

Поле направлене в кожній точці х вздовж напрямку х, тобто до металу. Максимальне значення поля спостерігається на межі розділу з металом.

, (2.30)

Інтегруючи рівняння (8), отримуємо електростатичний потенціал

(2.31)

Поскільки при x=0, ми взяли , тобто вибрали початок відліку потенціалу від рівня Ec₀, одержимо .

Абсолютне значення буде

. (2.32)

Величина має максимальне абсолютне значення

(2.33)

Як напруженість поля, так і потенціал пропорціональні , тобто зростають по абсолютному значенню із збільшенням концентрації донорів N_d.

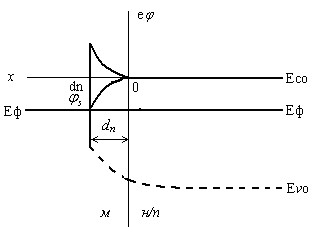
Рис.2.4. Зонна схема контакту метал- напівпровідник в стані термодинамічної рівноваги.

На рис. 2.4. якісно показано хід з врахуванням знака в області збідненого шару, а також хід потенціальної енергії електронів , які відповідають рівнянню (10). Квадратична залежність (або ) має зміст тільки для запірного шару, тому другу вітку параболи можна не враховувати.

Формули приведеного типу можна записати також в приміненні до діркового напівпровідника, який контактує з металом, якщо Ф_н/п>Ф_м .

Відмітимо, що припущення про те що об`ємний заряд є постійним є наближеним, особливо для внутрішньої області збідненого шару, поскільки там величина мала, так що експоненту в формулі (2.25), строго говорячи, можна не враховувати. Якщо вважати, що , то експоненту можна розкласти в ряд:

(2.34)

Якщо обмежитися двома першими членами ряду, одержимо:

. (2.35)

Якщо врахувати, що в даному випадку ,то

. (2.36)

Вибираємо напрямок відліку x від металу в глибину н/п. Приймаючи в глибині напівпровідника ,отримуємо =0, так як при віддаленні від межі розділу величина зменшується. Інша постійна . Тут є абсолютна величина потенціалу при x=0, який вибираємо виходячи із умови, коли стає справедливим нерівність , тобто в так званій квазінейтральній області. Якщо ця область простягається аж до поверхні, то .

Для квазінейтрального шару отримуємо:

(2.37)

Таким чином, дебаєвська довжина екранування L_D являє собою глибину проникнення поля в квазінейтральній області, на якій потенціал по абсолютному значенню зменшується в e раз. Для германію ( ) при 300К і n₀=10¹⁴см^-3 маємо L_D=4^.10^-5см.