Без доказательства

1.2.3. Масштабирование

Пусть f(x) имеет вид:, где a_i>0 сильно различаются между собой. Поверхности уровней функции вытянуты вдоль тех осей x_i, которым соответствуют малые a_i.

Для более эффективного применения градиентных методов необходимо превращение поверхностей уровня в круги

x₀

Заменой переменных можно добиться того, чтобы в новых переменныхy_i поверхности уровней стали сферами. Для этого достаточно принять (тогда все коэффициенты квадратичной формы- единицы).

В случае, когда f(x) не квадратичная, а достаточно гладкая функция общего вида выбирают:

Это диагональные элементы матрицы вторых производных. Это преобразование не превратит поверхности уровня в сферы, но в некоторых случаях позволит уменьшить их вытянутость. Гарантировано исправить вид функции f(x) можно, если учесть все, а не только диагональные элементы матрицы вторых производных и преобразования координат вида:

1.3. Метод Ньютона.

Разложим f(x) в ряд Тейлора до 2-го слагаемого включительно:

(*)

- вектор

- матрица Гессе, матрица вторых производных.

Будем рассматривать квадратичную аппроксимацию f(x), тогда получим (*) без то есть предполагаем, что f(x) квадратичная форма. Эта форма имеет единственную точку min, который является корнем уравнения f ’(x)=0.

В данном случае:

Метод Ньютона

Пример:

Сделаем одну итерацию метода Ньютона для квадратичной функции

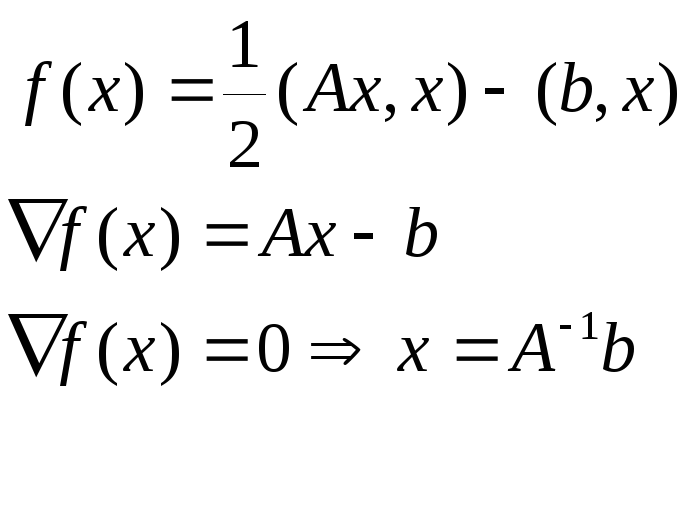
Этот пример показывает связь решения системы уравнений Ax-b = 0 и поиска минимума соответствующей функции f(x).

= A - матрица вторых производных.

Одна итерация метода Ньютона:

Но это точка минимума квадратичной функции. Таким образом для квадратичной функции метод Ньютона сходится за один шаг (матрица А должна быть положительно определена и симметрична, значения собственных чисел (растянутость) не играют роли).

Точка х₁ гораздо ближе к х* , чем в градиентных методах, но надо вычислить матрицу Гессе и обратить ее. Градиентный метод медленнее, но без дополнительных вычислений.

Оценим скорость сходимости метода Ньютона:

Теорема (о скорости сходимости метода Ньютона):

Пусть f(x) дважды дифференцируема, матрица удовлетворяет условию

Липшица с константой L :

f(x) сильно выпукла: 0 l I ² f(x) и начальное приближение удовлетворяет условию:

(есть требования к начальным условиям)

Тогда метод Ньютона сходится к х* с квадратичной скоростью

Доказательство:

Известно, что:

1)

Если на g’(x) удовлетворяет условию Липшица , то

Применим это отношение к ² f(x), тогда

Пусть x = x_k и

Дано (см. условие) тогда:

Таким образом .

Пусть q₁= (обозначим). Выразим полученное неравенство черезf(x₀)

.........................................................................

Для сильно выпуклых функций известно

Тогда

Теорема доказана.

Если начальные условия не удовлетворяют требованиям теоремы, то метод может не сходиться.

Понятие о скорости сходимости

Пусть метод обеспечивает выполнение следующего неравенства

, где d- наибольшее из чисел, для которых выполняется это условие, тогда d- скорость сходимости метода.

Если обозначить _k = , тогда скорость сходимости

d = , при _k0 (k ).

Пусть _k+1q _k, 0 q 1. Для этого случая d =1- геометрическая скорость. Для метода Ньютона _k+1= const _k²  d =2 - поэтому скорость называется квадратичной.

Сравнительная таблица достоинств и недостатков градиентного метода и метода Ньютона:

Метод	Достоинства	Недостатки
градиентный метод	1. Глобальная сходимость, т.е. слабые требования на исходные данные, точка х0 может быть далека от х*. 2. Слабые требования к f(x), только f’(x) нужна 3. Относительная простота вычислений	1. Медленная скорость сходимости (геометрическая сходимость, скорость сходимости d = 1).
метод Ньютона	1. Быстрая сходимость (квадратичная)	Локальная сходимость, т.е. начальное приближение должно быть достаточно близко к х*) Жесткие требования на саму функцию ( она должна быть дважды непрерывно дифференциируема). Большой объем вычислений, связанный с необходимостью вычисления матрицы вторых производных и ее обращения.

Полезен метод Ньютона в случае квадратичной функции (сходится за один шаг).

Число обусловленности локального min.

Пусть - поверхности уровнейf(x).

Рассмотрим следующую величину

Очевидно, что у окружности r_=1, а у эллипса r_>1 (увеличивается с увеличением растянутости).

Определение:

Числом обусловленности точки локального min называется . Это число дает основание для выбора метода.

Определение:

Говорят, что точка локального min плохо обусловлена, если число обусловленности велико, и хорошо обусловлена, если оно близко к 1.

Пример.

Пусть f(x) = 1/2 (Ax, x). А - диагональная матрица. Тогда число обусловленности есть отношение max диагонального элемента к min диагональному элементу.

Порядок применения методов.

На первом этапе применяются методы первого порядка, так как они обеспечивают глобальную сходимость (градиентные методы).

На втором этапе (мало) - методы второго порядка (Ньютона).

Перечисленные методы являются классическими, они редко применяются в чистом виде, но служат базой для других методов. Смысл модификации метода в том, чтобы использовать достоинства обоих методов, обходя недостатки.

Известен метод Марквардта-Левенберга

Если   - градиентные методы

 0- метод Ньютона.