5.1. Уравнение Эйлера-Лагранжа.
Лемма Дюбуа-Раймона:
Пусть для некоторой функции f, непрерывной на [a, b] , и для всех функций h , непрерывных на [a, b] вместе со своей производной и таких, что h(a) = h(b) = 0
справедливо:
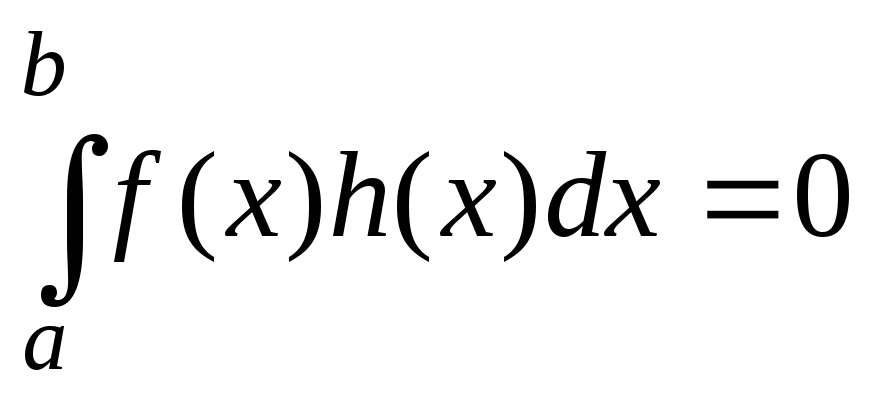,тогдаf
0 (б/д)
Разложим
J(
(x))
в ряд Тейлора в окрестности точки
= 0:
J(
(x))
= J(
)
+ 
+o()
SJ
= 
-первая
вариация функционала.
При
фиксированных
(x)
и (x)
функционал зависит от параметра
и необходимым
условием экстремума функционала
является:
SJ
= 0
Получим необходимое условие экстремума функционала в более конструктивной форме: функционал J, рассматриваемый как функция от , может быть записан в виде:
Тогда необходимое условие экстремума:
=
=
0
=
(по
частям)
=
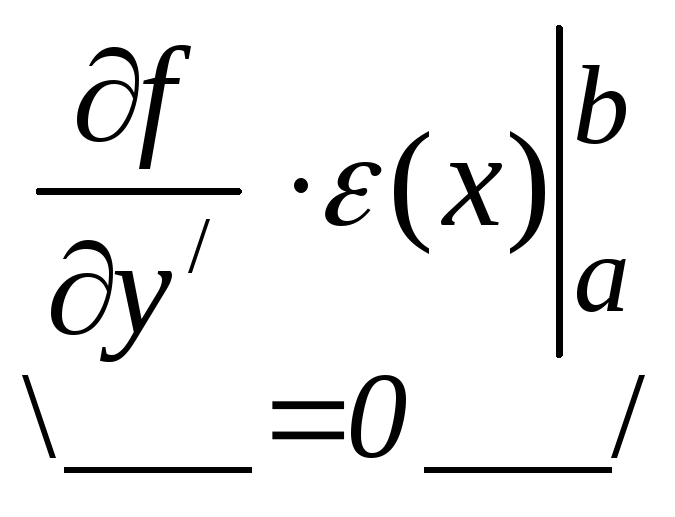
т.к.
=
=0
Это справедливо для любого (x) , дифференцируемого с краевыми условиями:
Отсюда с помощью леммы следует:
-
уравнение Эйлера-Лагранжа
Определение: Всякое решение уравнения Эйлера-Лагранжа называется
экстремалью.
Таким образом, функция, доставляющая экстремум функционалу находится среди экстремалей. Уравнение Эйлера-Лагранжа - необходимое условие экстремума.
Одно из достаточных условий локального минимума - условие Лежандра:
Обозначим
,
Уравнение Эйлера-Лагранжа:
Раскроем второй член выражения:
=
+
+
( формула дифф-я сложной функции)
Уравнение Эйлера-Лагранжа:
=
0 (*)
( если все производные существуют)
Отсюда следует, что в общем случае уравнение Эйлера-Лагранжа является нелинейным дифференциальным уравнением второго порядка. Поэтому его решение затруднено.
5.1.1. Частные случаи уравнения Эйлера-Лагранжа.
f (x, y) не зависит от производной
.
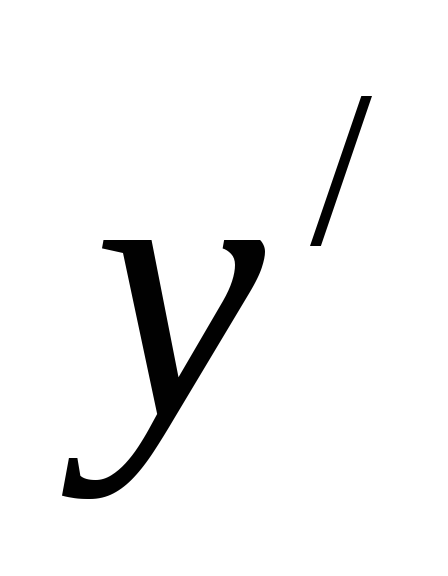Тогда
=
0
(
уравнение
Эйлера-Лагранжа)
f (x,
)
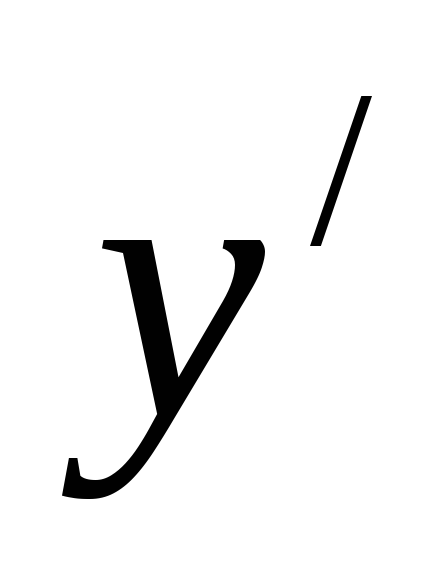не зависит отy:
=
0
0
f (y,
)
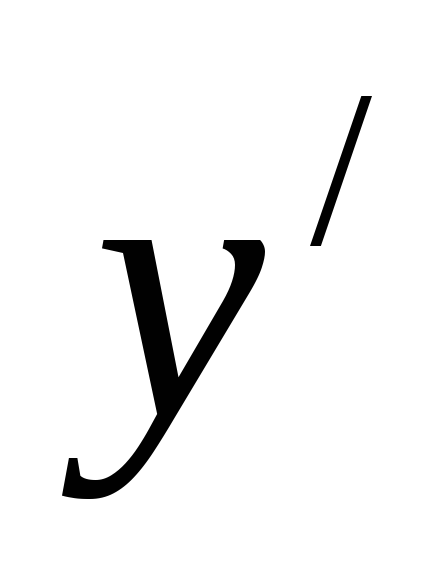не зависит отx:
(*)
0\
умножим
данное выражение на
\
(
)
0
Пример:
5.1.2. Задача о брахистохроне.
Как выбрать профиль горки, чтобы можно было скатиться с неё за минимальное время (трение отсутствует, под действием силы тяжести)?
Перерисуем для удобства рассмотрения :
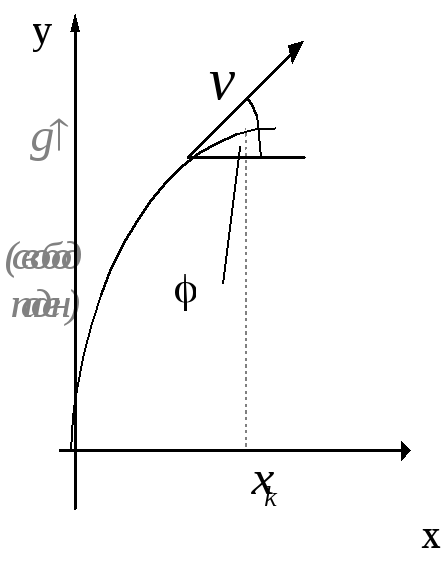
Здесь V –скорость, - угол наклона горки, g ускорение свободногопадения.
Справедливы следующие соотношения:
dx = V cos j dt (*)
tg
j
=
(x)
cos j
=
(1)
v-? (найдем формулу скорости)
Закон сохранения энергии для решения заданной задачи имеет вид:
=
mgy,
отсюда
V
=
(2)
Подставим (1) и (2) в (*), получим:
=
dt
Проинтегрируем обе части:
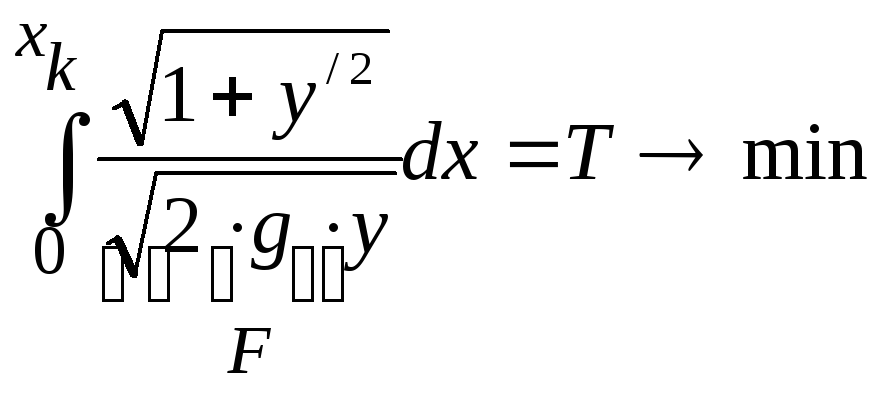(Т
– время спуска шарика.)
Итак, требуется найти функцию y=y(x), минимизирующую указанный выше интеграл.
Отметим,
что F
зависит от y
и
,
т.е. это третий частный случай уравнения
Эйлера - Лагранжа Þ
F
–
const - уравнение
Эйлера-Лагранжа для F(y,Y’).
Вынесем 2g из рассмотрения, т.к. на экстремум оно не влияет
Приведем к общему знаменателю:
Выберем
c
=
const
=
тогда
:
(**)
Это уравнение надо решить. Делаем подстановку:
=
tg
t
\
t-
вспомогательная переменная
\
Из (**) следует:
Интегрируем:
=
=
y через x выразить трудно.
Константы берутся из начальных условий.
Полученная кривая называется циклоидой.
График:
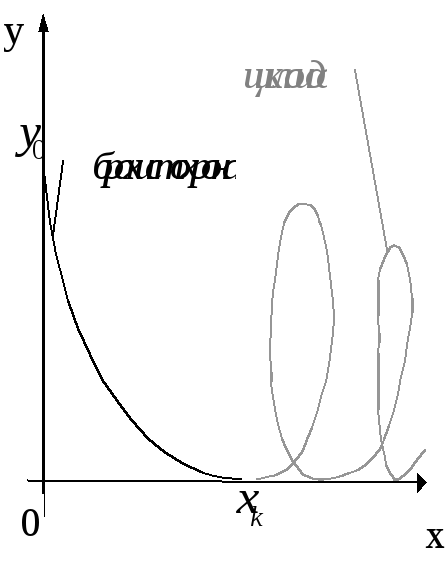
Брахистохрона (решение) является локальным минимумом.
Доказано,
что это глобальный минимум (
>0).