2.4. Двойственность звп

В формулировке теоремы Куна- Таккера прямые и двойственные переменные входят симметричным образом. Поэтому можно ожидать, что аналогичная симметрия существует и для задач оптимизации относительно прямых и двойственных переменных.

Введем функцию: g(x)=sup(x,), при0

Тогда очевидно ,что

g(x) =f(x), еслиg_i(x)0,i=1...m

g(x) =, в противном случае

Понятно, что (x,) =f(x)+(,g(x)),

Поэтому исходная ЗВП может быть записана в виде:

ming(x)-?, приxRⁿ

Эту задачу принято называть прямой.

Поступим аналогичным образом, поменяв роль переменных и операций maxиmin. Обозначимh()=inf , приxRⁿ

Задачу нахождения максимума функции h()-? при, называют двойственной.

Теорема двойственности:

Справедливы следующие соотношения двойственности:

1) f(x)h() xX,

2) Если выполнено условие теоремы Куна-Таккера, а пара (x*,*) является седловой точкой функции Лагранжа, то*-решение двойственной задачи.

* = argmaxh(),прииf(x* )=h(*)

3)Если для допустимых x*,* :f(x*)=h(*), то

x* =argminf(x), приxX– решение прямой задачи,

* = argmaxh(), при0 – решение двойственной задачи.

Доказательство:

1) f(x)f(x)+(,g(x))=(x,)inf(x,) =h(), приxRⁿ

2) Для всех 0 справедливо соотношение:

h(*)=inf(x,*) =(x* ,*)(x* ,)inf(x,) =h(),приxRⁿ

Отсюда * - решение двойственной задачи.

Но (x*,*) =f(x*)h(*)=f(x*)

3) На основании 1)f(x)h(*) = (на основании 2))f(x*)h()

тогда x*- прямое решение,*- двойственное решение

Продемонстрируем двойственность ЗВП на примере задачи линейного программирования (ЗЛП) , которая вкладывается в ЗВП.

Напомним, что функция fназывается вогнутой, если -fвыпуклая функция.

Определение. Функция, которая выпукла и вогнута одновременно, является афинной или линейной функцией.

2.4.1. Двойственность злп

Рассмотрим множество X=xRⁿ,x,Axb,b- вектор размерностиm,A- матрица размерностиmn.

f(x) = (c,x)- целевая функция (линейная)

ЗЛП: minf(x)-?, приxX- прямая задача линейного программирования.

Построим функцию Лагранжа.

=(c,x)+(₁,b-Ax)+( ₂,-x),₁R^m,₂Rⁿ (подгоняем подg_i(x)0).

Тогда min(c,x) =maxinf(c,x)+(₁,b-Ax)+(₂, -x), при₁0,₂0,xRⁿ = (см. метод модификации функции Лагранжа) =maxinf(c-A^T₁-₂,x)+(b,₁)

при ₁0,₂0,xRⁿ =

Примечание: (_1,Ax)=(A^T₁,x)

= max 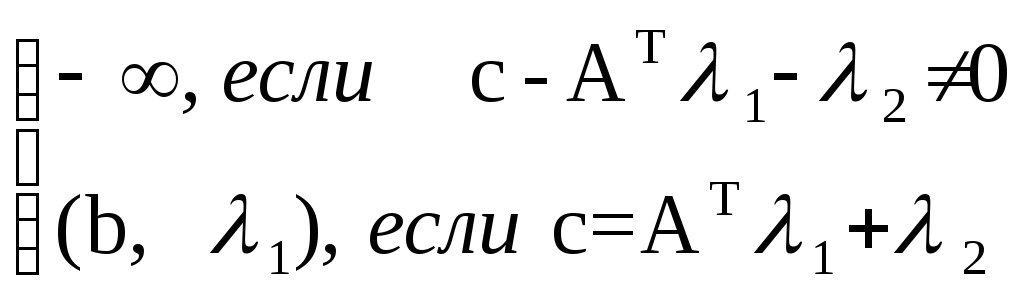, при₁0,₂0

= max(b,₁) (при₁0,₂0, с=A^T₁+₂) =max(b,₁) (при₁0, сA^T₁)

Таким образом, max(b,) = (c,x*), сA^T,0

max(b,), сA^T,0 - двойственная ЗЛП.

Таким образом, решение исходной ЗЛП может быть сведено к решению новой ЗЛП : максимизация (b,) по множеству, определенному условиями сA^T,

 0.

Утверждения:

1. Вектор состояния двойственной ЗЛП имеет размерностьm- количество ограничений в исходной задаче (размерность вектораAx).

2. Количество ограничений (кроме 0, неотрицательных) совпадает с размерностью вектора состояний в исходной задаче (вектораx).

3. Суммарное количество ограничений совпадает с (n+m) в обеих задачах.

4. Двойственная задача к двойственной задаче дает исходную задачу.

Когда какую задачу решать - зависит от числа ограничений и от размерности множества Х.

Утверждение:

Двойственные переменные можно рассматривать как коэффициент чувствительности целевой функции к изменению параметров задачи.

Пусть x* ,*- решения прямой и двойственной задач, причем эти решения единственны (достиг. в одной точке минимумxи в одной максимум)

Тогда f(x*) = (b,*), несколько изменимb:bb+bminувеличился на

(b,*). При сдвигеbградиенты не изменились,_iостались теми же.

Обозначим h(b) =minf(x),Axb,x0.

Тогда при малых b:

h(b+b) =h(b) + (b,*), следовательно приb0 получим:

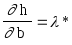, для компонент векторов