2.3.2. Метод условного градиента.

В очередной точке x^kлинеаризуют функциюf(x) (в этом «условность» метода, то есть линеаризация и есть «условие» в названии). Затем решают задачуminлинейной функции наXи найденную точкуиспользуют для выбора направления движения.

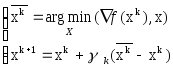
При этом предполагается:

1. Задача минимизации линейной функции на Xимеет решение.

2. Это решение может быть найдено достаточно просто, лучше всего в явной форме.

3. Нужно указать правило выбора _k. Можно_kопределить из условия наискорейшего спуска :

В этом случае последовательность x^kсходится к специальной точке. В частности для гладких функцийfверно:f(x*)-f* =o(1/k), гдеf* =minf(x) на множествеX.

2.3.3. Метод модифицированной функции Лагранжа.

Функцией Лагранжа в ЗВП называется функция

(x ,) = f(x)+f(x) + (,g(x)), где _i0.

Выше была доказана теорема о седловой точке:

Если выполняется соотношение

(x* ,)(x* ,*)(x,*)xRⁿ,0,

то точка x* является оптимальной точкой задачи выпуклого программирования.

Это соотношение можно записать иначе:

(*)(x* ,*) =(x,) =(x,) =f(x*)

Если назвать xпрямыми переменными, адвойственными, то видно, что прямые и двойственные переменные равноправны.

Теорема Куна- Таккера позволяет исходную задачу заменить задачей отыскания седловой точки функции Лагранжа, то есть задачи вида (x,).

Метод Эрроу-Гурвица ориентирован на поиск седловой точки функции (x,).

Метод Эрроу- Гурвица

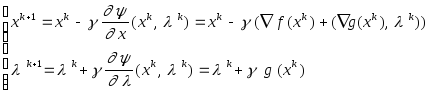
Сходимость таких методов затруднена в общей ситуации.

Метод модифицированной функции Лагранжа обладает лучшими характеристиками по сравнению с предыдущими методами.

Определим - модифицированная функция Лагранжа:

.

11. некоторый параметр (штраф)

+ - взятие положительной части.

Свойства модифицированной функции Лагранжа.

1. Если +k g(x)>0,то

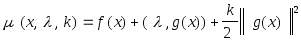
- добавка (штраф) за то, чтоg(x)>0.

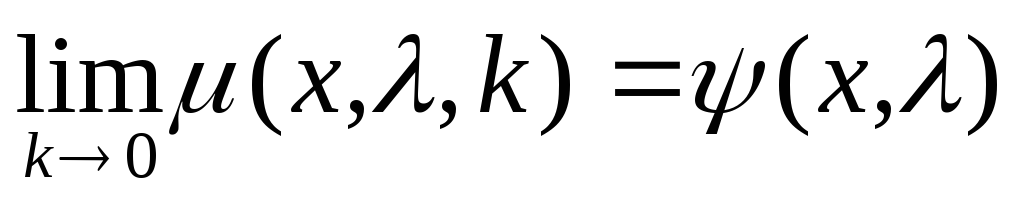2. (функция Лагранжа),

иначе

Метод модифицированной функции Лагранжа.

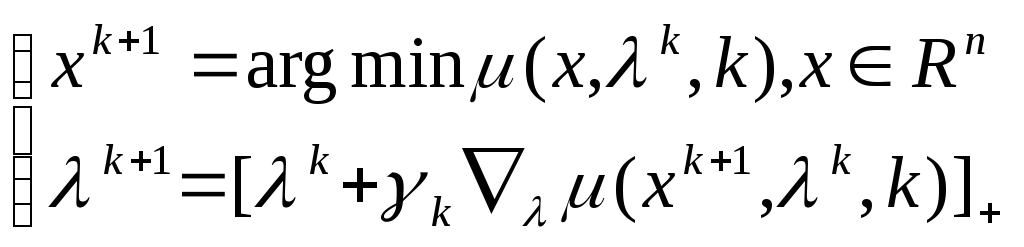
Метод сходится к (x* ,*) со скоростью геометрической прогрессии.

2.3.4. Метод штрафных функций.

Идея метода: Сведение задачи с ограничениями к последовательности задач без ограничений.

ЗНП:

min f(x), xX,

X = {xRⁿ, g_i(x) 0, i = 1...m}

Определение:

Функция (x), определенная и непрерывная всюду в Rⁿ , называется штрафной функцией для рассматриваемой задачи с ограничениями, если:

Строится однопараметрическое семейство функций:

, где  - скалярный параметр, принимающий строго положительные значения.

Алгоритм метода штрафных функций:

1. Выбираем убывающую последовательность 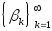положительных чисел, такую, что .

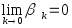2. Сопоставляем каждому _к из этой последовательности соответствующую функцию семейства (x,). Получаем последовательность функций (x,₁),..., (x,_k).

Пусть для каждой функции этой последовательности может быть решена задача безусловной минимизации (одним из рассмотренных ранее методов) :

.

Оказывается, что при некоторых условиях последовательность оптимальных точек для задач без ограничений может сходиться к оптимальной точке для исходной задачи с ограничениями: на Х.

Применяются различные штрафные функции. Наиболее распространена следующая штрафная функция:

, где - «срезка» функции:

=0, если 0

=, если>0

или