- •Тольяттинский государственный университет Физико-технический институт
- •Часть 2. Модуль 5
- •Содержание
- •Часть 2. Модуль 5. Раздел: постоянный электрический ток
- •Часть 2. Модуль 5. Раздел: магнитное поле в вакууме
- •Введение
- •Принятые условные обозначения
- •Часть 2. Модуль 5. Раздел: Постоянный электрический ток
- •Практическое занятие № 5
- •Тема: постоянный электрический ток. Законы ома
- •Содержание:
- •Основные формулы
- •Методические указания к решению задач
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Р Рис. 10 ешение
- •Решение
- •Р Рис. 13 ешение
- •Р Рис. 16 ешение
- •Задания для аудиторной работы
- •Задания для аудиторной самостоятельной работы Вариант № 1
- •Вариант № 2
- •Вариант № 3
- •Вариант № 4
- •Вариант № 5
- •Вариант № 6
- •Вариант № 7
- •Вариант № 8
- •Домашнее задание
- •Практическое занятие №6
- •Тема: постоянный электрический ток.
- •Правила кирхгофа. Закон джоуля-ленца
- •Содержание
- •Основные формулы
- •Методические указания к решению задач
- •1.Расчет характеристик разветвленных электрических цепей.
- •2. Задачи на расчет величины работы, мощности и теплоты можно разбить на три группы.
- •Примеры решения задач
- •Решение
- •Решение
- •Задания для аудиторной работы
- •Задания для аудиторной самостоятельной работы Вариант № 1
- •Вариант № 2
- •Вариант № 3
- •Вариант № 4
- •Вариант № 5
- •Вариант № 6
- •Вариант № 7
- •Вариант № 8
- •Домашнее задание
- •Часть 2. Раздел: Магнитное поле в вакууме
- •Практическое занятие № 7
- •Тема: магнитное поле в вакууме
- •Содержание
- •Основные формулы
- •Методические указания к решению задач
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •1 Случай
- •2 Случай
- •3 Рис. 50 случай
- •Д ано Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задания для аудиторной работы
- •Задания для аудиторной самостоятельной работы Вариант № 1
- •Вариант № 2
- •Вариант № 3
- •Вариант № 4
- •Вариант № 5
- •В Рис. 77 ариант № 6
- •Вариант № 7
- •Вариант № 8
- •Домашнее задание
- •Практическое занятие № 8 тема: движение заряженных частиц в магнитном поле. Работа по перемещению проводников с током или контуров с током в магнитном поле Содержание
- •Основные формулы
- •Методические указания к решению задач
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задания для аудиторной работы
- •Задания для аудиторной самостоятельной работы Вариант № 1
- •Вариант № 2
- •Вариант № 3
- •Вариант № 4
- •Вариант № 5
- •Вариант № 6
- •Вариант № 7
- •Вариант № 8
- •Домашнее задание
- •Приложения Единицы физических величин си, имеющие собственные наименования
- •Единицы электрических и магнитных величин
- •Удельное сопротивление ρ и температурный коэффициент α проводников
- •Плотность ρ твердых тел и жидкостей
- •Твердые тела
- •Диэлектрическая проницаемость ε
- •Множители и приставки для образования десятичных, кратных и дольных единиц и их наименований
- •Формулы алгебры и тригонометрии
- •Формулы дифференциального и интегрального исчислений
- •Литература
- •Электричество и магнетизм
- •Часть 2. Модуль 5 Разделы: «Постоянный электрический ток». «Магнитное поле в вакууме»
Решение
Рассмотрим
участок пространства между обкладками
конденсатора. Т.к. среда слабо проводящая,
будем считать, что разность потенциалов
электростатического поля есть величина
постоянная, участок - однородный. Тогда
разобьем этот участок на слои толщиной
![]() .
Элементарное сопротивление такого
тонкостенного цилиндрического слоя
радиуса
.
Элементарное сопротивление такого
тонкостенного цилиндрического слоя
радиуса
![]() и толщины
будет:
и толщины
будет:
![]() .
Т.к. слои соединены последовательно, то
результирующее сопротивление равно:
.
Т.к. слои соединены последовательно, то
результирующее сопротивление равно:
![]() .
.
Для
однородного участка цепи силу тока
найдем по закону Ома в интегральной
форме:
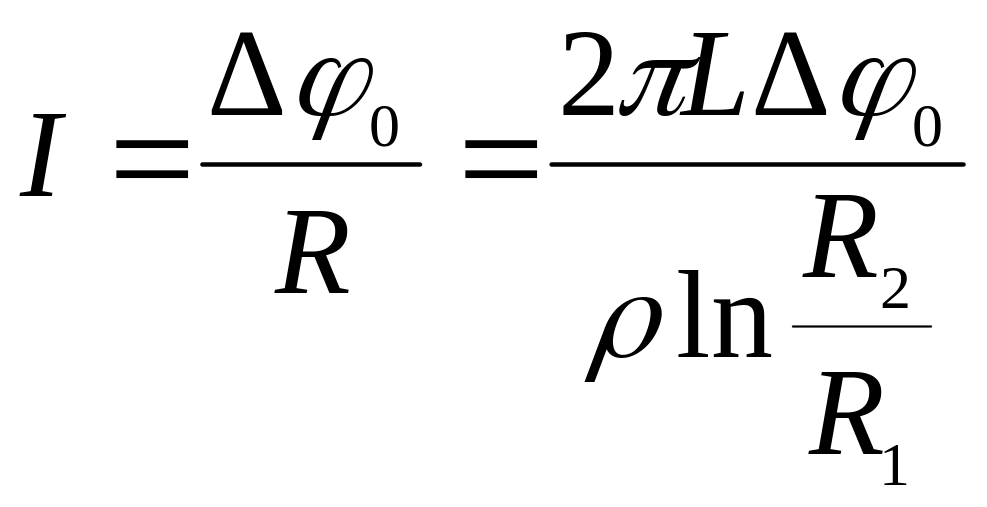 .
.
Проверка
размерностей: [R]
=![]() =Ом;
[I]
=
=Ом;
[I]
=
![]() = А.
= А.
Ответ:
;
Эта задача иллюстрирует применение метода дифференцирования и интегрирования (ДИ) к расчету характеристик электрической цепи- силы тока и сопротивления цепи.
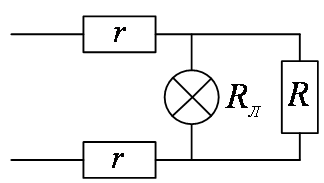
Пример 6. Определить сопротивление в цепи уличного освещения, которое состоит из достаточно большого числа одинаковых ячеек, состоящих из сопротивлений подводящих проводов и сопротивления лампы, соединенных как показано на рисунке 4.
Рис.
4
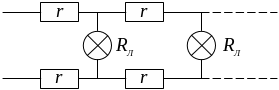
![]() – сопротивление
лампы,
– сопротивление
лампы,
![]() –
длина подводящих проводов между двумя
столбами,
– удельное сопротивление подводящих
проводов,
–
длина подводящих проводов между двумя
столбами,
– удельное сопротивление подводящих
проводов,
![]() – площадь поперечного сечения проводов.
– площадь поперечного сечения проводов.
Д ано Анализ
ано Анализ
Т.
к. цепь бесконечно длинная, то, отделив
одно звено, мы практически не изменим
общее сопротивление всей цепи. Обозначим
общее сопротивление цепи –
![]() .
Составим эквивалентную схему нового
соединения (рис. 5).
.
Составим эквивалентную схему нового
соединения (рис. 5).
Рис.
5![]()
![]()
Сопротивление
первой лампочки
![]() и общее сопротивление цепи
соединены параллельно, заменим их одним
сопротивлением
и общее сопротивление цепи
соединены параллельно, заменим их одним
сопротивлением
![]() :
:
![]() (1)
(1)
![]() (2)
(2)
С
 Рис.
6
Рис.
6
![]() (3).
Перепишем выражение (3) в виде (4):
(3).
Перепишем выражение (3) в виде (4):
![]() (4)
(4)
Решением уравнения (4) является:
![]() (5)
(5)
По
определению сопротивление длинного
проводника равно:
![]() (6)
(6)
Окончательно
получим:
![]() (Ом).
(Ом).
Ответ: (Ом).
Пример
7. Длинный
проводник круглого сечения радиусом r
сделан из материала, удельное сопротивление
которого зависит только от расстояния
r
до оси проводника как
![]() ,
где a
= const.
По проводнику течет ток I.
Найти:
,
где a
= const.
По проводнику течет ток I.
Найти:
Сопротивление единицы длины проводника.
Напряженность поля в проводнике.
Д ано Сделаем
рисунок
ано Сделаем
рисунок
r
Рис.
7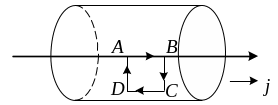
= а/r2
a = const
![]()
![]()
![]()
Решение
Рассмотрим
применение к решению задачи теоремы о
циркуляции вектора
![]() ЭСП
и
закона Ома в дифференциальной форме
для однородного участка цепи.
ЭСП
и
закона Ома в дифференциальной форме
для однородного участка цепи.
Проводник, рассматриваемый в задаче, неоднородный, т.к. его сопротивление меняется с изменением расстояния от оси проводника.
Докажем, что напряженность электростатического поля ( = const) является постоянной во всех точках сечения данного проводника.
Для доказательства воспользуемся теоремой о циркуляции вектора напряженности ЭСП.
Замкнутый контур внутри проводника выберем в виде прямоугольника, одна сторона которого совпадает с осью проводника (рис. 7).
![]() (1);
(1);
![]()
![]() (3).
(3).
Т.к.
АВ=СD,
то
= const,
т.е. напряженность постоянна во всех
точках проводника. Из закона Ома в
интегральной форме сопротивление
проводника равно:
![]() .
(4). Но
.
(4). Но
![]() и тогда
и тогда
![]() (5).
(5).
Теперь
запишем закон Ома для однородного
участка цепи в дифференциальной форме:
![]() .(6)
.(6)
По
определению:
![]() (7). Отсюда:
(7). Отсюда:
![]() (8).
(8).
Т.к.
проводник имеет круглое сечение радиусом
,
то:
![]() ,
тогда
,
тогда
![]() (площадь тонкого кольцевого слоя, в
пределах которого величину плотности
тока можно считать одинаковой) будет
равна:
(площадь тонкого кольцевого слоя, в
пределах которого величину плотности
тока можно считать одинаковой) будет
равна:
![]() (9).
(9).
Учитывая,
что
![]() а
а
![]() ,
то вынеся постоянный множитель
,
то вынеся постоянный множитель
![]() из-под знака интеграла, получим:
из-под знака интеграла, получим:
![]()
Выразим искомую величину напряженности электрического поля из соотношения (10):
(11)
![]()
Теперь
найдем сопротивление проводника из
закона Ома в интегральной форме для
однородного участка цепи:
![]() (12), учитывая, что
(13),
(12), учитывая, что
(13),
тогда:
![]()
Проверка
размерности:
![]()
![]() ;
;
![]() =
=
![]() ;
[a]
=
;
[a]
=
![]() .
.
Ответ:
![]()
![]() ;
;
![]()
![]() .
.
Пример
8. Ток
короткого замыкания источника тока с
ЭДС
![]() составляет
40 А.
Найти величину сопротивления, которое
нужно включить во внешнюю цепь, чтобы
получить от этого источника ток силой
1 А.
составляет
40 А.
Найти величину сопротивления, которое
нужно включить во внешнюю цепь, чтобы
получить от этого источника ток силой
1 А.
Д ано Решение
ано Решение
Величину
внутреннего сопротивления источника
найдем из выражения для величины тока
короткого замыкания:
![]()
![]() (1)
(1)![]() (2)
(2)
![]()
![]()
![]()
Из
закона Ома для полной цепи:
![]() (3) выразим величину сопротивления
цепи, подставив значение внутреннего
сопротивления источника тока в формулу
(3). Получим:
(3) выразим величину сопротивления
цепи, подставив значение внутреннего
сопротивления источника тока в формулу
(3). Получим:
![]() (4)
(4)
Проверка
размерности:
![]()
Расчет:
числовое значение сопротивления -
![]()
Ответ:
![]() .
.
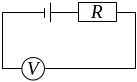
Пример 9. Можно ли с помощью вольтметра измерить ЭДС источника?
Рис.
8