Основные элементы зубчатой передачи. Термины, определения и обозначения

Одноступенчатая зубчатая передача состоит из двух зубчатых ко­лес - ведущего и ведомого. Меньшее по числу зубьев из пары колес назы­вают шестерней, а большее колесом. Термин «зубчатое колесо» является об­щим. Параметрам шестерни (ведущего колеса) приписывают при обозначе­нии нечетные индексы (1, 3, 5 и т. д.), а параметрам ведомого колеса — четные (2, 4, 6 и т. д.).

Зубчатое зацепление характеризуется следующими основными пара­метрами:

d_a — диаметр вершин зубьев;

d_r — диаметр впадин зубьев;

d_a — начальный диаметр;

d — делительный диаметр;

р_t — окружной шаг;

h — высота зуба;

h_a — высота ножки зуба;

с — радиальный зазор;

b — ширина венца (длина зуба);

е_t — окружная ширина впадины зуба;

s_t — окружная толщина зуба;

 — межосевое расстояние;

а — делительное межосевое расстояние;

Z — число зубьев.

Делительная окружность - окружность, по которой обкатывается ин­струмент при нарезании. Делительная окружность связана с колесом и де­лит зуб на головку и ножку.

Основные элементы зубчатых колес представлены на рис.15.

 

Рис. 15. Геометрические параметры цилиндрических зубчатых колес

 

Модулем зубьев т называется часть диаметра делительной окружности, приходящаяся на один зуб.

Модуль является основной характеристикой размеров зубьев. Для пары зацепляющихся колес модуль должен быть одинаковым.

Линейную величину, в   раз меньшую окружного шага зубьев, называют окружным модулем зубьев и обозначают т:

.

Размеры цилиндрических прямозубых колес вычисляют по окружному модулю, который называют расчетным модулем зубчатого колеса, или про­сто модулем; обозначают буквой т. Модуль измеряют в миллиметрах. Мо­дули стандартизованы (табл. 3).

 

Таблица 3. Стандартные значения модулей

1-й ряд	2-й ряд	1-й ряд	2-й ряд	1-й ряд	2-й ряд	1-й ряд	2-й ряд
1	1,125	3	3,5	10	11	32	36
1,25	1,375	4	4,5	12	14	40	45
1,5	1,75	5	5,5	16	18	50	55
2	2,25	6	7	20	22	60	70
2,5	2,75	8.	9	25	28	80	90

Примечание. При назначении модулей первый ряд значений следует предпочитать второму.

 

Ниже приведены определения остальных параметров зацепления.

Начальная окружность — каждая из взаимокасающихся окружностей зубчатых колес передачи, принадлежащая начальной поверхности данного зубчатого колеса.

Начальные окружности являются сопряженными, т.е. это понятие от­носится к паре колес, находящихся в зацеплении (к передаче). При измене­нии межосевого расстояния   начальные диаметры тоже соответственно изменяются, так как   равно сумме радиусов этих окружностей. Таким об­разом, у пары колес, находящихся в зацеплении, может быть сколько угод­но начальных окружностей, в то время как для отдельно взятого зубчатого колеса понятие начальной окружности вообще лишено смысла.

По делительному диаметру d окружные шаги соответствуют стандарт­ному модулю т. Для цилиндрических прямозубых колес, например,   или  .

Основными называются окружности, по которым развертываются эвольвенты,  очерчивающие профили зубьев.

Окружностями выступов и впадин называются окружности, ограничивающие вершины и впадины зубьев.

Линией зацепления называется геометрическое место точек контакта зубьев в зацеплении. В эвольвентном зацеплении линия зацепления - прямая, нормальная к профилю зубьев в полюсе зацепления и касательная к основным окружностям.

Углом зацепления   называется угол между линией зацепления и перпендикуляром к линии центров.

Углом наклона спирали зубьев косозубых шестерен   называется угол между осью зуба и образующей делительного цилиндра или конуса.

Для определения основных параметров зубчатой передачи принимают делительный радиус. Если межосевое расстояние в передаче равно сумме делительных радиусов, то начальные и делительные окружности в этом случае совпадают. В дальнейшем рассматривается именно такой частный случай зацепления.

Высота зуба h — радиальное расстояние между окружностями вершин и впадин зубчатого колеса:

.

Головка зуба — его часть, расположенная между делительной окружно­стью цилиндрического зубчатого колеса и окружностью вершин зубьев; h — высота головки зуба.

Ножка зуба — часть зуба, расположенная между делительной окружно­стью и окружностью впадин (высота ножки зуба h_f).

Радиальный зазор — расстояние между поверхностями вершин зубьев и впадин шестерни и колеса:

.

Окружная толщина зуба s_t — расстояние между разноименными профи­лями зуба по дуге концентрической окружности зубчатого колеса.

Ширина венца b — наибольшее расстояние между торцами зубьев ци­линдрического зубчатого колеса по линии, параллельной его оси.

Межосевое расстояние   — расстояние между осями зубчатых колес передачи.

 

           

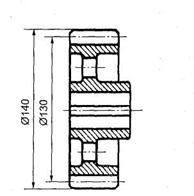
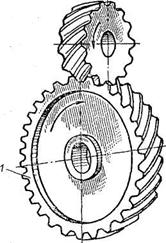
Рис. 16                                                             Рис.17

 

Основная теорема зубчатого зацепления. Понятия о линии и полюсе зацепления. Профилирование зубьев

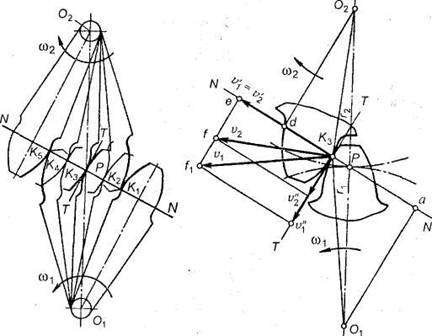
Для обеспечения нормальной работы пары зубчатых колес с постоянным передаточным числом профили зубьев должны быть очерчены по кривым, подчиняющимся определенным законам. Эти законы вытека­ют из основной теоремы зацепления, сущность которой заключается в следующем.

Пусть имеется пара зубчатых колес с центрами О₁ и О₂, вращающихся соответственно с угловыми скоростями   и  . На рис.18, а показаны сложения, которые последовательно занимает пара сопряженных (эвольвентных) зубьев в процессе их зацепления; прямую О₁О₂ называют межосевой линией зубчатой передачи. Проведем в точках касания зубьев К₁, К₂, К₃, ... общие нормали к профилям. Все эти нормали NN должны пересекать межосевую линиюО₁О₂ в постоянной точке Р. Эту точку называют полюсом зацепления; ее положение на межосевой линии определяется отношением уг­ловых скоростей колес, т. е. их отношением:

.

 

                                                                           а)                                                                               б)

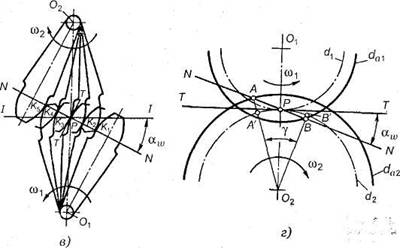
Рис. 18. Элементы зубчатого зацепления

 

Основную теорему зацепления можно сформулировать так: общая нор­маль к профилям зубьев в точке их касания пересекает межосевую линию в точке Р, называемой полюсом зацепления и делящей межосевое расстояние на отрезки, обратно пропорционально угловым скоростям.

Следствие: для обеспечения постоянного передаточного отношения по­ложение полюса Р на линии центров должно быть постоянным.

В процессе работы сопряженных (эвольвентных) профилей точка их касания все время перемещается по прямой NN. Эту прямую называют линией зацепления.

Место (точку) входа в зацепление и выхода из него сопряженных зубь­ев можно определить при следующем геометрическом построении.

Возьмем произвольное межосевое расстояние О₁О₂ (рис.18, г) и раз­делим его в произвольном отношении  . Радиусами О₂Р и O₁P проведем начальные окружности зубчатых колес через точку Р, касатель­ную ТТ кэтим окружностям и линию NN — нормаль к боковым поверхно­стям зубьев — под углом   и касательной ТТ. Угол   называют углом за­цепления; в СНГ   принят 20°.

Примем произвольную высоту головки зубьев и проведем радиусами, равными   и  , окружности выступов зубчатых колес (высота го­ловки зуба шестерни и колеса должна быть одинаковой). При направлении вращения колес, указанном на рисунке, зубья войдут в зацепление в точке А (точке пересечения нормали с окружностью выступов колеса) и выйду: из зацепления в точке В (точке пересечения нормали с окружностью вы­ступов шестерни).

Все точки касания сопряженных зубьев будут лежать на участке АВ ли­нии зацепления. Участок АВ называется рабочим участком линии зацепле­ния.

Необходимое условие непрерывности зацепления: дуга зацепления должна быть больше шага. В противном случае при выходе из зацепления одной пары зубьев вторая пара еще не войдет.

Длина линии зацепления q_a — отрезок линии зацепления, отсекаемый окружностями вершин зубьев сопряженных колес. Он определяет начало и конец зацепления пары сопряженных зубьев. Длина зацепления — актив­ная часть линии зацепления.

Коэффициент торцового перекрытия   — отношение длины линии за­цепления к шагу:

.

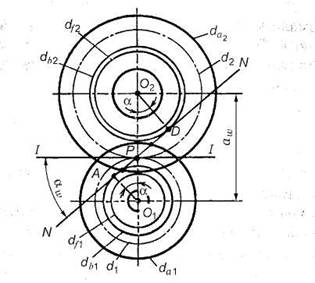
Рис. 19. Геометрические параметры зубчатой передачи

 

Полюс зацепления Р (см. рис. 18, б) сохраняет неизменное положе­ние на линии центров О₁О₂. Следовательно, радиусы О₁P (r₁) и О₁P (r₁) также неизменны. Окружности радиусов r₁ и r₂ называют начальными (делитель­ными). При вращении зубчатых колес эти окружности пе­рекатываются одна по другой без скольжения, о чем свидетельствует ра­венство их окружных скоростей   (см. доказательство основной теоремы зацепления). Теоретически боковые поверхности зубьев (профи­ли) могут быть очерчены любыми кривыми, удовлетворяющими основному закону зубчатого зацепления. Такие профили называют сопряженными.

В современном машиностроении для построения сопряженных профилей применяют ограниченное число кривых.

Профили зубьев должны быть технологичными, т.е. такими, чтобы их можно было получить в производственных условиях наиболее простыми методами. Из теоретически возможных профилей преимущественное применение получили эвольвентные профили (см. рис. 18, б), так как такие про­фили проще обработать и они обладают большими преимуществами. Эвольвентное зацепление предложено Эйлером более 200 лет назад. Это зацепление по сравнению с другими имеет следующие преимущества: при изменении межосевого расстояния не нарушается правильность их зацепления (не изменяется передаточное число); это зацепление может быть использовано и в сменных колесах.

В зацеплении М.Л. Новикова рабочие профили зубьев очерчены дуга­ми окружностей (рис. 20, 21). По сравнению с эвольвентными передачами зацепления Новикова могут при одних и тех же габаритных размерах передавать в 1,5-2 раза большую мощность. Ввиду сложности изготовления и монтажа передачи с зацеплением Новикова пока нашли применение только в специальном машиностроении.

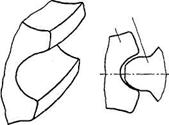
Рис. 20. Колесо с зацеплением М. Л. Новикова

 

Рис. 21.  Кинематика зацепления зубчатых колес

 

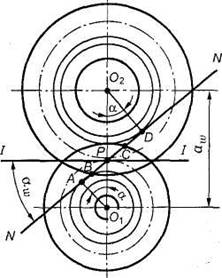
Рис.22

 

Краткие сведения о корригировании зацеплений

Форма эвольвентного профиля зубьев при заданном угле инстру­мента   и модуле зависит от числа зубьев z (рис. 23): с уменьшением чис­ла зубьев увеличивается кривизна эвольвентного профиля и соответствен­но уменьшается толщина зубьев у основания и вершины.

Если число зубьев z меньше некоторого предельного значения z_min, то при нарезании зубьев происходит подрезание ножек зуба (рис. 23, z= 10), в результате чего в опасном сечении зуб значительно ослабляется, снижа­ется его прочность на изгиб, а также уменьшается рабочая часть ножки, что увеличивает изнашивание зубьев и уменьшает коэффициент их пере­крытия.

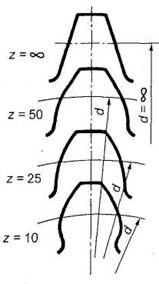
Рис.23. Формы зубьев  эвольвентного профиля

 

Минимальное число зубьев шестерни, у которой исключено подреза­ние зубьев, без сдвига инструмента реечного типа, определяется по фор­муле  , где  — угол профиля зуба рейки. Для стандартного зацепления  = 20°,  = 17. При больших окруж­ных скоростях передачи для уменьшения шума для гедукторов   принимают   число   зубьев   шестерни z = 20 ÷ 30.

Для устранения явлений подрезания зубьев и улуч­шения параметров передачи применяют корригирование. Корригирование зубьев производят на обычных станках стандартным инструментом. Разница в из­готовлении зубчатых колес с некорригированными и корригированными зубьями заключается в том, что для последних инструмент устанавливают с некоторым дополнительным смещением по отношению к оси заготовки.

При этом по сравнению с нормальным эвольвентным  зацеплением  профили  корригированных зубьев получаются другими, т.е. используются для данной передачи более выгодные участки эвольвенты той же основной окружности. Соответственно заготовки этих колес должны быть измененного диаметра.

Коррекция зацепления может быть высотной или угловой. Осущест­вляется она смещением инструментальной рейки (рис. 24) на размер   при нарезании зубьев (положительное смещение рейки — от центра зубча­того колеса, отрицательное — к центру).

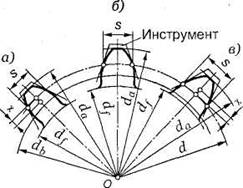
Рис.24. Профили корригированных колес

 

Высотное корригирование. Шестерню изготовляют с положительным ко­эффициентом смещения X₁, а колесо с отрицательным — X₂. Суммарный коэффициент смещения  . При высотной коррекции изменя­ется соотношение между высотой головки ножки зубьев, общая же высота зубьев не изменяется. Межосевое расстояние   и угол зацепления   так­же остаются неизменными.

Угловое корригирование отличается от высотного тем, что  . При   и   толщина зубьев по делительным окружностям   и диаметры вершин зубьев   увеличатся как у шестерни, так и у колеса. Для обеспече­ния нормального зацепления колеса необходимо раздвинуть на величину   (при этом начальные окружности отличаются от делительных). При увеличении межосевого расстояния   угол зацепления   возрастает.Угло­вое корригирование имеет значительно большие возможности, чем высот­ное, поэтому применяется чаще.

Более подробные сведения по корригированию зацепления приведены в специальной литературе.