
- •Будівельна механіка. Конспект лекцій для студентів напряму “Будівництво” денної та заочної форм навчання/ я.Д.Кислюк, д.Я.Кислюк. - Луцьк: лнту, 2008.
- •Тема 1. Основні положення будівельної механіки. Кінематичний аналіз споруд
- •1.1. Розрахункові схеми та основні елементи споруд
- •1.2. Кінематичний аналіз споруд
- •Тема 2. Розрахунок балок та простих рам на нерухоме навантаження
- •2.1. Загальні положення визначення внутрішніх зусиль в балках
- •2.2. Порядок та методи розрахунку балок
- •2.3. Залежності між побудованими епюрами
- •2.4. Багатопрольотні статично визначні балки
- •2.5. Розрахунок шарнірно-консольної балки
- •2.6. Статично визначні рами
- •2.7. Особливості розрахунку складених рамних систем
- •Тема 3. Прості плоскі ферми
- •3.1. Поняття про ферму та особливості її роботи
- •3.2. Класифікація ферм
- •3.3.Визначення зусиль в стержнях ферм
- •Тема 4. Розрахунок трьохшарнірних систем
- •4.1. Види трьохшарнірних систем
- •4.2. Визначення опорних реакцій трьохшарнірної арки
- •4.3. Визначення внутрішніх зусиль
- •Тема 5. Розрахунок балок на рухоме навантаження
- •5.1. Загальні положення розрахунку конструкцій на рухоме навантаженняю
- •5.2. Лінії впливу опорних реакцій балок
- •5.3.Лінії впливу внутрішніх зусиль для балок
- •5.4. Визначення зусиль за допомогою ліній впливу
- •Тема 6. Розрахунок ферм на рухоме навантаження
- •Тема 7. Розрахунок трьохшарнірних систем на рухоме навантаження
- •При побудові лінії впливу поперечної сили qk для перерізу к арки використаємо вираз
- •Побудова ліній впливу за допомогою нульових точок.
- •Тема 8. Загальні методи визначення переміщень
- •8.1.Робота зовнішніх сил
- •8,2. Теорема про взаємність робіт
- •8.4. Формула переміщень
- •8.5. Переміщення від зміни температури
- •8.6. Техніка знаходжень переміщень
- •8.7. Переміщення статично визначених систем, визваних зміщенням опор
- •Література
- •43018 М. Луцьк, вул. Львівська, 75.
Тема 4. Розрахунок трьохшарнірних систем
4.1. Види трьохшарнірних систем
Трьохшарнірна система складається з двох дисків (/ і //), з’єднаних за допомогою одного шарніра один з одним (шарнір С на рис. 4.1) і двома шарнірами із землею (шарніри А і В). Земля може розглядатися як третій диск і тому трьохшарнірна система є з'єднанням трьох дисків за допомогою трьох шарнірів, не розташованих на одній прямій. Таке з'єднання, як відомо, є геометрично незмінним .

Рис 4.1
Якщо диски / і // (рис. 4.2) є стержнями з криволінійною віссю (а), то трьохшарнірна система називається трьохшарнірною аркою; якщо дисками / і // є прямолінійні (б) або ламані (в) стержні, то система називається трьохшарнірною рамою; у випадку, коли диски / і // виявилися наскрізними конструкціями (фермами), система називається трьохшарнірною арочною фермою(г).Відстань І між центрами опорних шарнірів трьохшарнірної арки називається прольотом, а відстань f від середнього шарніра до прямої, що з’єднує опорні шарніри, — стрілою підйому арки
Трьохшарнірна система може бути симетричною і несиметричною щодо вертикальної осі. В симетричній системі середній шарнір С розміщений на осі симетрії, а опорні шарніри А і В — на одному рівні.
Опори А і В в несиметричній системі можуть бути розміщені на різних рівнях (рис. 4.3).

Рис 4.2

Рис 4.3
У трьохшарнірних арках і рамах одна з шарнірно нерухомих опор може бути замінена шарнірно рухомою з вертикальним опорним стержнем. У цьому випадку для забезпечення геометричної незмінності вводиться затяжка, яка і сприймає розпір.
4.2. Визначення опорних реакцій трьохшарнірної арки
Реакції Ra і Rb опор трьохшарнірної системи характеризуються кожна двома параметрами — величиною і напрямом (або, наприклад, величинами горизонтальної і вертикальної складових Н і V); отже, опорні реакції трьохшарнірної системи характеризуються чотирма параметрами, наприклад, величинами сил HA, HB, VA, VB . Вони можуть бути визначені з трьох рівнянь рівноваги всіх сил, діючих на систему (включаючи і опорні реакції), і четвертого рівняння,

Рис 4.4
що виражає рівність нулю моменту всіх сил, діючих на ліву або праву частину системи, відносно шарніра С. Отже, трьохшарнірна система є статично визначною.
Вертикальні складові опорних реакцій VА і VВ визначають з рівнянь моментів відносно опор :
![]()
де ai — плече сили Pi відносно точки А.
Правильність визначення VА і VB перевіряють, склавши рівняння ΣY=0. З рівняння ΣХ=0 стає відомим, що НА=Нв=H. Значення розпору аналітично визначають з рівняння ΣMcлів =0, або ΣMcправ =0:
![]()
оскільки
![]()
то
![]()
При дії на трьохшарнірну систему вертикального навантаження горизонтальні складові НА і НВ реакцій опор А і В, так звані розпором, не рівні нулю; у зв'язку з цим трьохшарнірні системи відносять до розпірних.
4.3. Визначення внутрішніх зусиль
Внутрішніми зусиллями, що виникають в поперечних перерізах арки, є згинаючі моменти М, поперечні сили Q і подовжні сили N. Їх визначають при навантаженнях, які діють на арку ліворуч або праворуч даного перерізу.При визначенні внутрішніх зусиль і побудові епюр цих зусиль використовують правила знаків (за винятком знака поздовжньої сили, яка в арках вважається додатньою при стиску) приведені для балок.При розрахунку арок у виразах доцільно позначити вісь, співпадаючу з дотичної до осі арки в даному перерізі u (замість х в балок), перпендикулярну до неї v (замість y), а проекції сил на ці осі відповідно U і V.
З урахуванням висловленого виразу для арок рівняння рівноваги приймають вигляд:

В цих виразах, що входять під знаки сум моменти зовнішніх сил додатні при обертанні за годинниковою стрілкою, проекції V — коли направлені знизу вгору, а проекції U — коли направлені зліва направо.
Визначимо за допомогою виразів внутрішні зусилля в поперечному перерізі k арки, показаної на рис. 4.5, де х і y — координати точки k осі арки; — кут між дотичної до осі арки в точці k і горизонталлю; Ру та Рx — відповідно вертикальна і горизонтальна проекції сили Р; хр і уp — координати точки прикладення сили Р.

Рис 4.5
В отримані вирази
Q,
М
і N
під знаки сум входять проекції Ру
і Рx
всіх сил Р,
прикладених до арки зліва перерізу k.
Для перерізу k
, показаного на рис. 4.5,
під знак кожної
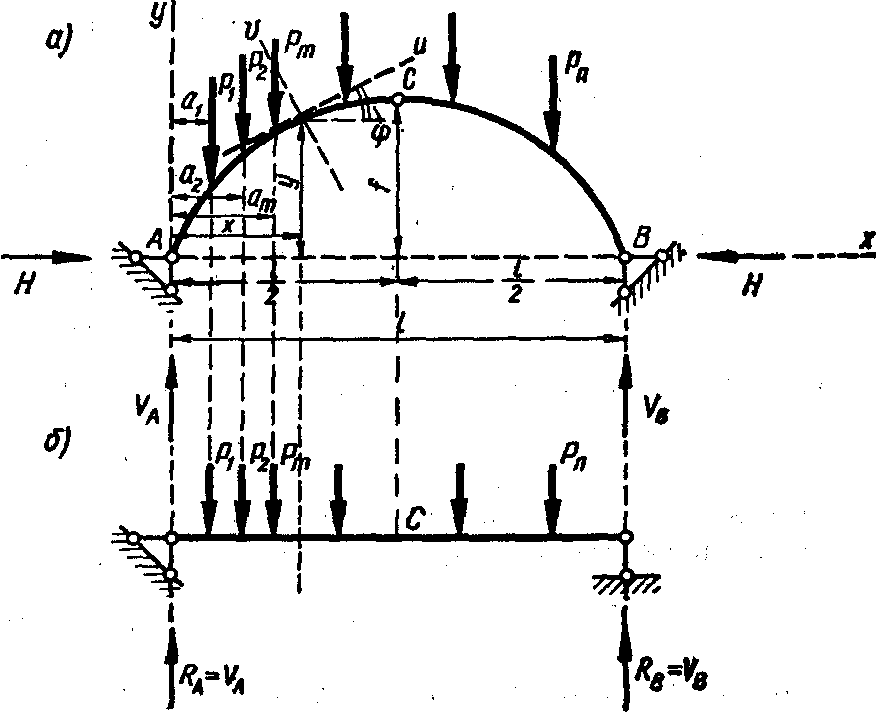
Рис.4.6
суми входить лише одна проекція Рy, або Px. Аналогічним шляхом зусилля Q, М і N можуть бути виражені і як проекція правих сил.
При дії на арку тільки вертикального навантаження (рис.4.6,а) горизонтальні проекції Рx; рівні нулю, проекції Рy рівні Р, а розпір НA = HB= Н; тому вирази приймають спрощений вигляд:
![]()
![]()
NX=![]() .
.
У трьохшарнірній арці із затяжкою Va=V0a, Vb=V0b; зусилля в затяжці визначають з рівняння
ΣMcлів=0
![]()
Згинаючий момент М, поперечна Q і подовжня N сили в будь-якому перерізі трьохшарнірної арки із затяжкою будуть рівні:
а) для ділянок нижче затяжки
![]()
![]()
![]()
б) для ділянок вище затяжки
![]()
Як видно з наведених вище формул в арці, порівняно з балкою істотно зменшується згинальний момент і поперечна сила, що є результатом впливу розпору. Наявність в арках розпору викликає необхідність встановлення масивних опор або затяжок, здатних сприймати великі горизонті зусилля.
Раціональним контуром осі арки називається такий, при якому крива тиску від заданого нерухомого навантаження співпадає з віссю арки; отже, при цьому навантаженні у всіх перерізах арки згинаючий момент рівний нулю. Якщо ординати y і η осі арки і кривої тиску визначаються відповідно рівняннями
y=f(x) та =(x),
то умовою того, що вісь арки має раціональний контур, є тотожність: y=
При дії на арку тільки вертикального навантаження

Рис 4.7
чисельник
останньої формули рівний згинаючому
моменту в простій балці в перетині з
абсцисою х,
тобто![]() ,
а тому
,
а тому
![]()
Використовуючи співвідношення y=, одержуємо наступне рівняння раціональної осі арки:
![]()
Отже, при вертикальному навантаженні вісь арки буде раціональною, якщо її контур міняється за законом зміни балочного моменту.
