5.2. Ортогональное дополнение

Определение. Два множества F и G векторов евклидова пространства E называются ортогональными, если каждый вектор из F ортогонален каждому вектору из G.

Определение. Пусть F – подпространство E. Совокупность всех векторов подпространства E, ортогональных подпространству F, называется ортогональным дополнением подпространства F.

Всякое ортогональное дополнение является, в свою очередь, линейным подпространством.

Всякое произвольное евклидово пространство E разлагается в прямую сумму своего произвольного подпространства F и его ортогонального дополнения

Примеры

1. Требуется найти базис ортогонального дополнения подпространства L, натянутого на векторы

, ,

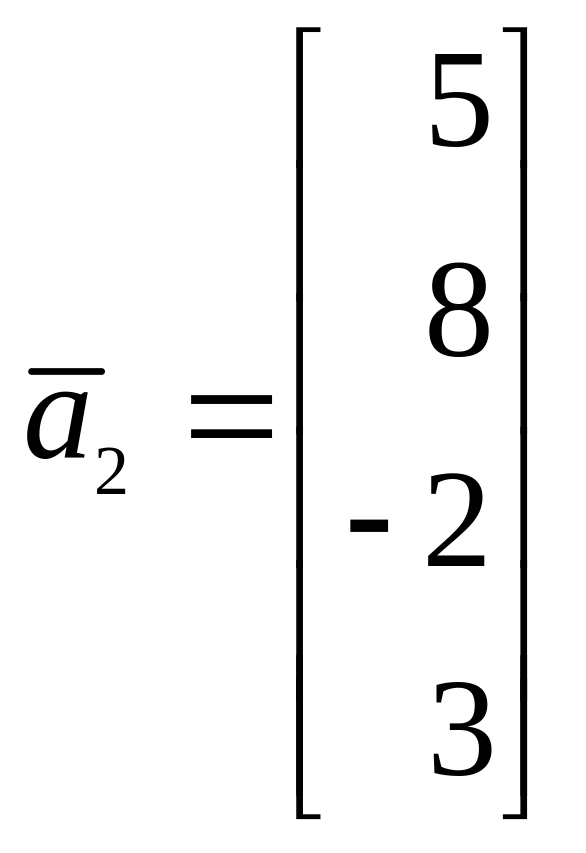Будем считать, что базис, относительно которого заданы векторы, ортонормированный. По определению, если , то . Далее, каждый вектор из должен быть ортогонален к . Для этого достаточно, чтобы . Расписывая скалярные произведения, получим три уравнения относительно координат вектора

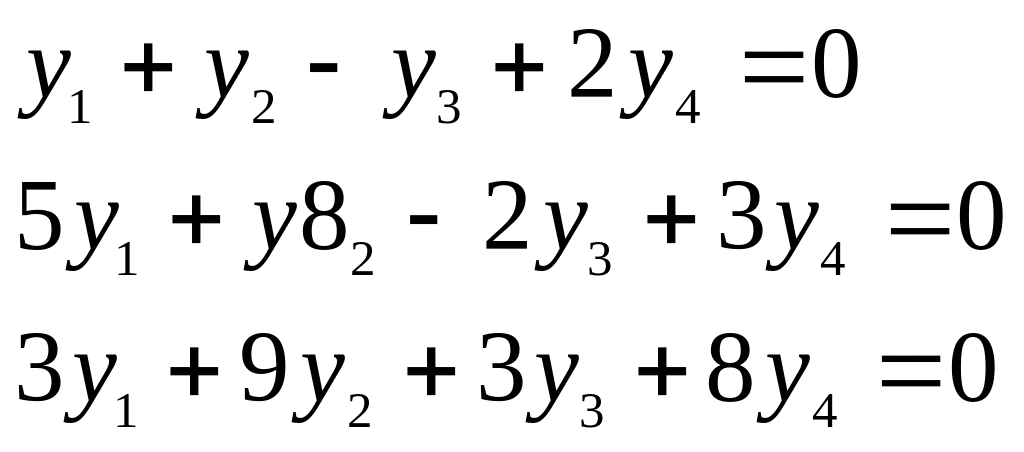
Совокупность решений этой системы и образует ортогональное дополнение. За базис в можно принять любую фундаментальную систему решений. Например, вектор .

2. Линейное подпространство задано уравнениями

Требуется найти уравнения, которые задают ортогональное дополнение .

Пусть , . Тогда . Этому условию удовлетворяют два линейно независимых вектора и , которые образуют коэффициенты системы уравнений, задающей F. Далее, . Ранг системы равен 2. Значит и, так как , то . Поэтому найденные векторы можно принять за базис в , и есть линейная оболочка данных векторов. Далее задача решается так же как в примере из § 3. Дословно повторяя решение, получим следующую систему уравнений

которая и задает .

5.3. Проектирование вектора на подпространства

Пусть . Тогда всякий вектор можно представить в виде , где и . Вектор называется ортогональной проекцией вектора x на подпространство L, а вектор называется ортогональной составляющей вектора .

Пусть и — расстояние между векторами , тогда

Таким образом, ортогональная проекция есть ближайший к вектору подпространства L. Часто используются следующие обозначения , .

Укажем в заключение как вычисляются координаты вектора . Пусть — базис в L. Так как , то . Поэтому

Отсюда имеем, что в случае ортонормированного базиса

Примеры

1. Найти ортогональную проекцию и ортогональную составляющую вектора на линейное подпространство L, натянутое на векторы . Все векторы заданы координатами относительно ортонормированного базиса.

, , ,

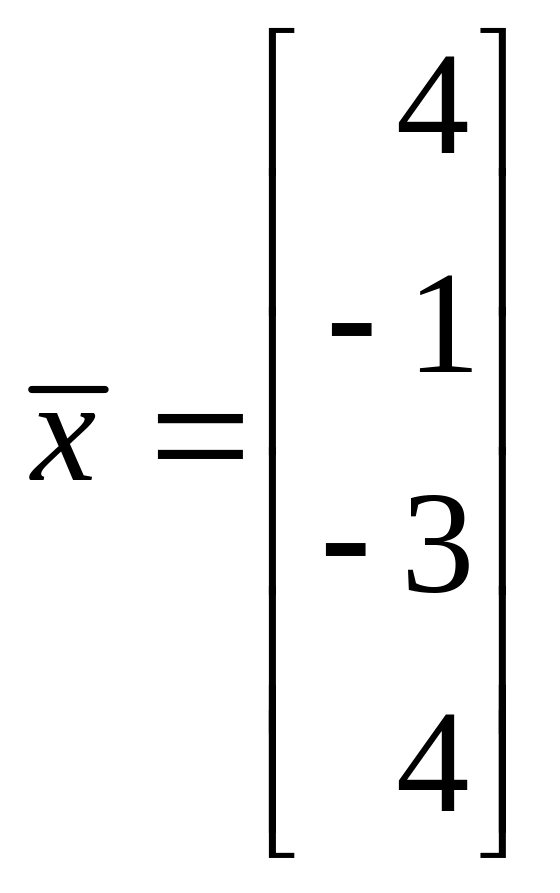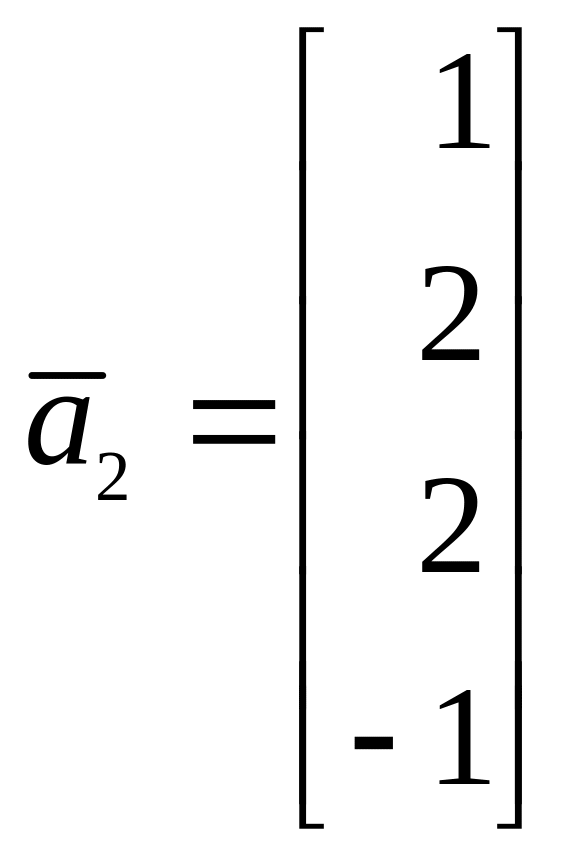Нетрудно убедиться, что и что за базис можно принять векторы и . Нам будет удобно перейти к ортонормированному базису в L. Применяя процедуру ортогонализации к векторам и , получим ортонормированный базис в L:

,

Заметьте, что векторы и линейно выражаются через и и, значит, также принадлежат L. Имеем теперь

2. Требуется найти расстояние от точки, заданной вектором до плоскости (линейного многообразия), заданной системой уравнений

Расстояние между точкой и множеством L определится следующим образом

Для вычисления расстояния удобно перейти к параметрическому уравнению плоскости. Имеем и поэтому всякий вектор представляется в виде

где — фиксированный радиус-вектор точки плоскости; и — базис направляющего линейного подпространства, которое задается соответствующей однородной системой. Решая уравнение, получим, например,

, ,

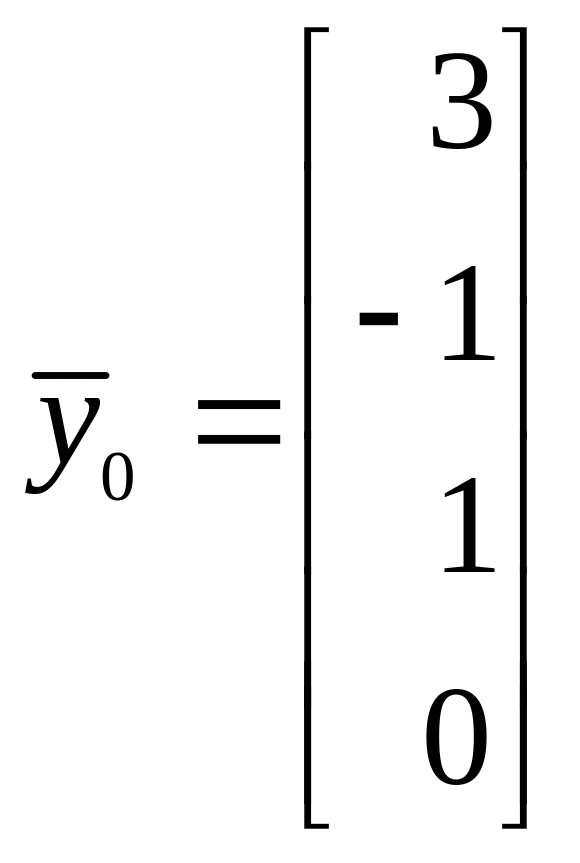Затем

Векторы и принадлежат направляющему подпространству M плоскости L. Вектор . Так как , а , то

Правая часть этого неравенства и есть искомое расстояние. Осталось вычислить вектор и найти его норму. Проделав для этого аналогичные вычисления и вычислив длину вектора, получим, что .

3. Пусть — ортонормированная система векторов евклидова пространства E_n. Нужно доказать, что для любого вектора имеет место неравенство Бесселя

с равенством тогда и только тогда, когда , т.е. векторы образуют ортонормированный базис в E_n.

Так как — ортонормированная система, то ее всегда можно векторами достроить до ортонормированного базиса в E_n. Разложим вектор по этому базису. Имеем

Далее,

или

С равенством тогда и только тогда, когда . Исключение составляют случаи, когда или когда принадлежит линейной оболочке векторов .