Метод Лагранжа

Задача состоит в вычислении какого–либо частного решения линейного неоднородного дифференциального уравнения с непрерывными коэффициентами и непрерывной правой частью.

Рассмотрим линейное неоднородное дифференциальное уравнение

y⁽ⁿ⁾ + a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' + a₀(x)y = f(x).

с непрерывными на [a; b] коэффициентами и непрерывной правой частью.

Предположим, что известна фундаментальная система y₁(x), y₂(x),..., y_n(x) решений соответствующего однородного уравнения   y⁽ⁿ⁾ + a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' + a₀(x)y = 0.

Будем искать частное решение неоднородного уравнения в виде

y*(x) = C₁(x) y₁(x) + C₂(x) y₂(x) + ... + C_n(x) y_n(x) ,

где C₁(x), C₂(x) , ... , C_n(x) — неизвестные, n раз дифференцируемые на [a; b] функции. Их называют варьируемые постоянные общего решения однородного уравнения.

Справедливо следующее утверждение.

Пусть y₁(x), y₂(x),..., y_n(x) — фундаментальная система решений однородного уравнения   y⁽ⁿ⁾ + a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' + a₀(x)y = 0 с непрерывными на отрезке [a; b] коэффициентами. Если правая часть f(x) неоднородного уравнения   y⁽ⁿ⁾ + a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' +a₀(x)y = f(x) непрерывна на [a; b], то его частное решение можно искать в виде

y*(x) = y(x,C₁,..., C_n) = C₁(x) y₁(x) + C₂(x) y₂(x) + ... + C_n(x) y_n(x) .

Неизвестные функции C₁(x), C₂(x) , ... , C_n(x) находятся из системы

Такой метод отыскания частного решения неоднородного уравнения называется методом вариации произвольных постоянных илиметодом Лагранжа.

Подробнее (кому нужно)

Посмотрим как можно найти методом Лагранжа частное решение для уравнения 2–го порядка y'' + a₁(x)y' + a₀(x)y = f(x) с нерерывными коэффициентами и непрерывной правой частью.

Предположим, что известна фундаментальная система y₁(x), y₂(x) решений соответствующего однородного уравнения   y'' + a₁(x)y' + a₀(x)y = 0.

Будем искать частное решение неоднородного уравнения в виде

y*(x) = C₁(x) y₁(x) + C₂(x) y₂(x),

где C₁(x), C₂(x) — такие неизвестные, дважды дифференцируемые на [a; b] функции.

Для того чтобы подставить функцию y*(x) в исходное уравнение, найдём сначала первую производную y*(x):

(y*(x))' = C₁'(x) y₁(x) + C₁(x) y₁'(x) + C₂'(x) y₂(x) + C₂(x) y₂'(x).

Будем искать C₁(x), C₂(x) такими, чтобы C₁'(x) y₁(x) + C₂'(x) y₂(x) = 0 и, следовательно,

(y*(x))' = C₁(x) y₁'(x) + C₂(x) y₂'(x).

Тогда

(y*(x))'' = C₁'(x) y₁'(x) + C₁(x) y₁''(x) + C₂'(x) y₂'(x) + C₂(x) y₂''(x).

Подставим выражения для производных в уравнение:

y'' + a₁(x)y' + a₀(x)y ≡ C₁'(x) y₁'(x) + C₁(x) y₁''(x) + C₂'(x) y₂'(x) + C₂(x) y₂''(x) + a₁(x)(C₁(x) y₁'(x) + C₂(x) y₂'(x)) + a₀(x)(C₁(x) y₁(x) + C₂(x)y₂(x)) = f(x).

После простых преобразований имеем:

C₁(x)(y₁'' + a₁(x)y₁' + a₀(x)y₁) + C₂(x)(y₂'' + a₁(x)y₂' + a₀(x)y₂) + C₁'(x) y₁'(x) + C₂'(x) y₂'(x) = f(x).

Но поскольку y₁(x), y₂(x) — решения однородного уравнения   y^'' + a₁(x)y' + a₀(x)y = 0, то

C₁'(x) y₁'(x) + C₂'(x) y₂'(x) = f(x).

Для неизвестных функций C₁(x), C₂(x) получили систему линейных дифференциальных уравнений второго порядка:

Определитель этой линейной относительно C₁'(x), C₂'(x) системы — это отличный от нуля на [a; b] вронскиан фундаментальной системы решений.

Следовательно, система имеет единственное решение, которое можно выписать в явном виде (имеем два дифференциальных уравнения первого порядка):

Эти дифференциальные уравнения первого порядка с разделяющимися переменными легко интегрируются:

Неизвестные варьируемые постоянные найдены — найдено частное решение линейного неоднородного уравнения второго порядка.

Пример

Найдём методом Лагранжа (методом вариации произвольных постоянных) частное решение линейного неоднородного дифференциального уравнения второго порядка

с непрерывными на (e, ∞) коэффициентами и непрерывной правой частью.

Фундаментальную систему решений соответствующего однородного уравнения образуют функции y₁(x) = ln x , y₂(x) = x.

Будем искать частное решение неоднородного уравнения в виде y*(x) = C₁(x) lnx + C₂(x) x:

Подставим выражения для производных в уравнение:

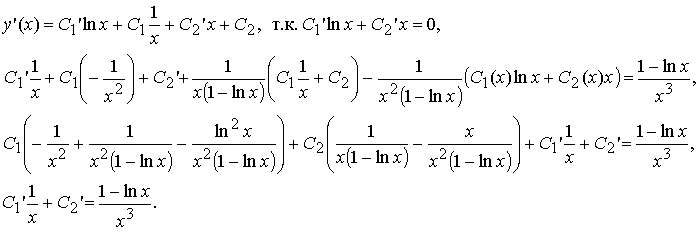
Для неизвестных функций C₁(x), C₂(x) получили систему линейных дифференциальных уравнений второго порядка:

Окуда имеем:

И тогда частным решением исходного уравнения второго порядка является функция y*(x) = C₁(x) lnx + C₂(x) x:

Построение частного решения неоднородного ДУ с постоянными коэффициентами при специальной правой части.

Рассмотрим линейное неоднородное дифференциальное уравнение

y⁽ⁿ⁾ + a_n-1y^{(n - 1)} + ... + a₁y' + a₀y = f(x). (1)

Коэффициенты a_n-1, ... , a₁, a₀ — десйствительные числа, f(x) — непрерывная на [a, b] правая часть.

Общее решение этого уравнения имеет вид y(x) = C₁y₁(x) + C₂y₂(x) + ... + C_ny_n(x) + y*(x),

где С₁, С₂, ..., С_n — произвольные постоянные, y₁(x), y₂(x), ..., y_n(x) — фундаментальная система решений однородного уравнения, y*(x) — частное решение неоднородного уравнения.

 

Если правая часть уравнения — квазимногочлен — функция вида

f(x) = exp(αx)M_m(x) или

f(x) = exp(αx)(M_m(x)cos(βx) + N_n(x)sin(βx)), β<>0.

Здесь M_m(x) — многочлен степени m, N_n(x) — многочлен степени n, α и β — действительные числа то частное решение уравнения (1) имеет вид

y*(x) = x^rexp(αx)P_m(x) ( r- кратность корня α в харак.урав)

или

y*(x) = x^rexp(αx)(P_k(x)cos(βx) + Q_k(x)sin(βx)),

где P_k(x) и Q_k(x) — многочлены степени k = max(n, m) с неизвестными коэффициентами, r- кратность корня α+iβ в харак.урав.

P_k(x) = p_kx^k + p_k-1x^k-1 + ... + p₁x + p₀, Q_k(x) = q_kx^k + q_k-1x^k-1 + ... + q₁x + q₀.

Для того чтобы найти неизвестные коэффициенты многочленов P_k(x) и Q_k(x) , подставляем y*(x) = exp(αx)(P_k(x)cos(βx) + Q_k(x)sin(βx)) в уравнение и приравниваем в правой и левой части полученного равенства коэффициенты при

exp(αx)cos(βx), exp(αx)sin(βx), xexp(αx)cos(βx), xexp(αx)sin(βx),  x²exp(αx)cos(βx), x²exp(αx)sin(βx), ...,   x^kexp(αx)cos(βx), x^kexp(αx)sin(βx).

Полученная таким образом система 2k + 2 уравнений относительно 2k + 2 неизвестных имеет единственное решение.

 

Метод подбора применяется к ограниченному, но достаточно широкому классу правых частей, поскольку квазимногочленами являются функции вида:

M_k(x),  M_k(x)exp(αx),  M_k(x)cos(βx),   M_k(x)sin(βx),  exp(αx)(M_m(x)cos(βx) + N_n(x)sin(βx)).  

Подробнее (кому нужно)

Частное решение y*(x) можно найти методом подбора, если правая часть уравнения — квазимногочлен — функция вида

f(x) = exp(αx)(M_m(x)cos(βx) + N_n(x)sin(βx)).

Здесь M_m(x) — многочлен степени m, N_n(x) — многочлен степени n, α и β — действительные числа.

Метод подбора вычисления частного решения линейного неоднородного уравнения с квазимногочленом в правой части состоит в следующем.

Внимательно смотрим на правую часть уравнения и записываем число α ± βi.

Затем составим характеристическое уравнение однородного уравнения и найдем его корни. Возможны два случая: среди корней характеристического многочлена нет корня, равного числу α ± βi (нерезонансный случай) и среди корней характеристического многочлена есть r корней, равных числу α ± βi ( резонансный случай).

Рассмотрим нерезонансный случай (среди корней характеристического многочлена нет корня, равного числу α ± βi) . Тогда частное решение уравнения будем искать в виде

y*(x) = exp(αx)(P_k(x)cos(βx) + Q_k(x)sin(βx)),

где P_k(x) и Q_k(x) — многочлены степени k = max(n,m) с неизвестными коэффициентами,

P_k(x) = p_kx^k + p_k-1x^k-1 + ... + p₁x + p₀, Q_k(x) = q_kx^k + q_k-1x^k-1 + ... + q₁x + q₀.

Для того чтобы найти неизвестные коэффициенты многочленов P_k(x) и Q_k(x) , подставим y*(x) = exp(αx)(P_k(x)cos(βx) + Q_k(x)sin(βx)) в уравнение и приравняем коэффициенты при

exp(αx)cos(βx), exp(αx)sin(βx), xexp(αx)cos(βx), xexp(αx)sin(βx),  x²exp(αx)cos(βx), x²exp(αx)sin(βx), ...,   x^kexp(αx)cos(βx), x^kexp(αx)sin(βx).

Доказано, что полученная таким образом система 2k + 2 уравнений относительно 2k + 2 неизвестных имеет единственное решение.

Рассмотрим резонансный случай (среди корней характеристического многочлена есть r корней, равных числу α ± βi) . Тогда частное решение уравнения будем искать в виде

y*(x) = exp(αx)(P_k(x)cos(βx) + Q_k(x)sin(βx))x^r,

где P_k(x) и Q_k(x) — многочлены степени k = max(n,m) с неизвестными коэффициентами.

Для того чтобы найти неизвестные коэффициенты многочленов P_k(x) и Q_k(x) , подставляем y*(x) = exp(αx)(P_k(x)cos(βx) + Q_k(x)sin(βx))x^rв уравнение и приравниваем коэффициенты при

exp(αx)cos(βx), exp(αx)sin(βx), xexp(αx)cos(βx), xexp(αx)sin(βx),  x²exp(αx)cos(βx), x²exp(αx)sin(βx), ...,   x^kexp(αx)cos(βx), x^kexp(αx)sin(βx).

 

Пример. Уравнением колебаний называют линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами

Однородное уравнение y'' + ω₀²y = 0 описывает свободные колебания материальной точки с частотой ω₀².

Неоднородное уравнение — колебания материальной точки под действием внешней периодической силы Fcosω₀x, частота которой ω₀ совпадает с частотой свободных колебаний частицы (резонанс).

Найдём общее решение уравнения колебаний в случае, когда частота свободных колебаний совпадает с частотой внешней вынуждающей силы.

Характеристическое уравнение однородного уравнения λ² + ω₀² = 0 имеет пару комплексно сопряжённых корней λ_1,2 = ± i ω₀.

Фундаментальную систему решений однородного уравнения образуют функции cosω₀x, sinω₀x. Общее решение однородного уравнения имеет вид

y(x, C₁, C₂) = C₁cosω₀x + C₂sinω₀x.

Правая часть уравнения — квазимногочлен exp(αx)(M_m(x)cos(βx) + N_n(x)sin(βx))≡Fcosω₀x , у которого α = 0, β = ω, M_m(x)=M₀ = F, N_n(x)= 0, α ± iβ = iω₀.

Среди коренй характеристического уравнения есть одна пара комплексно сопряжённых корней, равная α ± iβ = iω₀: λ_1,2 = ± i ω₀.

Поэтому будем искать частное решение неоднородного уравнения y*(x) в виде y*(x) =( A cosω x + B sin ω x)x.

Подставим в уранение:

y = (A cosω x + B sin ω x)x,

y' = (−Aω sinω x + B ωcos ω x)x + (A cosω x + B sin ω x),

y'' = (−Aω² cosω x − Bω² sin ω x)x + 2(−Aω sinω x + B ωcos ω x)x ,

y'' + ω₀²y = (−Aω² cosω x − Bω² sin ω x)x + 2(−Aω sinω x + B ωcos ω x)x + ω₀²(A cosω x + B sin ω x)x = 2Bω₀cosω₀ x − 2A sin ω₀ x = Fcos ω₀x.

Приравняв коэффициенты в левой и правой части уравнения  2Bω₀cosω₀ x − 2 A sin ω₀ x = Fcos ω₀x, получим A = 0, B = F/2ω₀и тогда частное решение неоднородного уравнения

Теперь можно записать общее решение неоднородного уравнения