Практична робота №4

Тема: Числові характеристики випадкової величини.

Мета: Навчитися знаходити математичне сподівання, дисперсію та середнє квадратичне відхилення дискретних та неперервних випадкових величин.

ХІД РОБОТИ

1. Розвязати задачі відповідно варіанта.

2. Зробити висновок.

3. Підготуватися до захисту практичної роботи за контрольними запитаннями.

Теоретична частина з прикладами виконання

практичних завдань

Величина називається випадковою, якщо в наслідок проведення експерименту під впливом випадкових факторів вона набуває того чи іншого можливого числового значення з певною ймовірністю.

Якщо множина можливих значень випадкової величини є зчисленною то таку величину називають дискретною. У противному разі її називають неперерваною.

Випадкові величини визначаються великими літерамі латинського алфавіту X, Y, Z,…, а їх можливі значення – малими x,y,z, … .

Для опису випадкової величини необхідно навести не лише множину можливих її значень, а і указати, з якими ймовірностями ця величина набуває того чи іншого можливого значення.

З цією метою вводять поняття закону розподілу ймовірностей.

Співвідношення, що встановляє зв'язок між можливими значеннями випадкової величини та відповідними їм ймовірностями, називають законом розподілу випадкової величини.

Закон розподілу дискретної випадкової величини X можна задати в табличній формі або за допомогою імовірнісного многокутника.

У разі табличної форми запису закону подається послідовність можливих значень випадкової величини Х, розміщених у порядку зростання, та відповідних їм ймовірностей:

Х = хі	х1	х2	х3	….	xk
Р(Х = хі) = рі	р1	р2	р3	….	рk

Оскільки випадкові події (Х = х_j) і (Х = х_m) є між собою несумісними то необхідною є така умова:

(1)

Рівність (1) називають умовною нормування для дискретної випадкової величини Х. Наведену таблицю називають рядом розподілу.

Приклад 1. Закон розподілу дискретної випадкової величини Х задано таблицею

Х = хі	2,5	3	4,5	5	5,5	6
Р(Х = хі) = рі	а	2а	а	3а	а	2а

Знайти ймовірність можливих значень випадкової величини Х: х₁ = 2,5; х₃ = 4,5; х₄ = 5; х₅ = 5,5; х₆ = 6.

Розв’язання. За умовою нормування (1) дістанемо:

Отже, закон розподілу дискретної випадкової величини набуває такого вигляду

Х = хі	2,5	3	4,5	5	5,5	6
Р(Х = хі) = рі	0,1	0,2	0,1	0,3	0,1	0,2

Дискретний закон розподілу ймовірностей можна унаочнити графічно.

Для цього візьмемо систему координат (р_і , х_і) відклавши на осі абсцис можливі значення випадкової величини х_і, а на осі ординат імовірності р_і цих можливих значень. Точки з координатами (х_і, р_і) послідовно сполучимо відрізками прямої. Утворену при цьому фігуру називають ймовірнісним многокутником.

Приклад 2. За заданим у табличній формі законом розподілу дискретної випадкової величини Х:

Х = `хі	- 2,5	1	3,5	5	6,5	8
Р(Х = хі) = рі	0,1	0,2	0,1	0,3	0,2	0,1

побудувати імовірнісний многокутник.

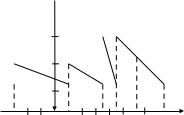
Розв’язання. Імовірнісний багатокутник зображено на рис.1

р_і

0,3

0,2

0,1

2,5 0 1 3,5 5 6,5 8 ^Х_і

Рисунок 1- Ймовірносний багатокутник

Сума ординат імовірнісного многокутника завжди дорівнює одиниці.

Функція розподілу ймовірностей (інтегральна функція) та її властивості

Закон розподілу ймовірностей можна подати ще в одній формі, яка придатна і для дискретних, і для неперервних випадкових величин, а саме: як функцію розподілу ймовірностей випадкової величини F(x), так звану інтегральну функцію.

Функцію аргументу х, що визначає ймовірність випадкової події Х < х, називають функцією розподілу ймовірностей:

F(x) = P(X < x) (2)

Цю функцію можна тлумачити так: унаслідок експерименту випадкова величина може набути значення, меншого за х.

Н априклад, F(5) = P(X < 5) означає, що в результаті експерименту випадкова величина Х (дискретна чи неперервна) може набути значення, яке міститься ліворуч від х = 5, що ілюструє рис.2

F(5) = P(X < 5)

-3 -2 -1 0 1 2 3 4 5 6 Х

Рисунок 2 - F(5) = P(X < 5)

Розглянемо властивості F(x):

1. 0 ≤ F(x) ≤ 1. Ця властивість випливає з означення функції розподілу.

2. F(x) є не спадною функцією, а саме F(x₂) ≥ F(x₁), якщо x₂ > x₁.

Із другої властивості F(x) випливають наведені далі висновки:

1. Імовірність того, що випадкова величина Х набуде можливого значення Х = х , дорівнює приросту інтегральної функції F(x) на цьому проміжку:

Р(α ≤ Х ≤ β) = F(β) - F(α).

2. Якщо випадкова величина Х є неперервною, то ймовірність того, що вона набуде конкретного можливого значення, завжди дорівнює 0:

Р(X = x_і) = 0

Отже для неперервної випадкової величини Х справджуються такі рівності:

Р(α < Х < β) = Р(α ≤ Х < β) = Р(α < Х ≤ β) = Р(α ≤ Х ≤ β)

Якщо можливі значення випадкової величини Х належать обмеженому проміжку 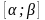, то

F(x) = 0 x ≤ a

F(x) = 1 x > b

Приклад 3. Закон розподілу дискретної випадкової величини Х задано таблицею:

Х = хі	-4	-1	2	6	9	13
Р(Х = хі) = рі	0,1	0,2	0,1	0,3	0,1	0,2

Побудувати F(x).

Розв’язання. Згідно з властивостями F(x), дістанемо наведені далі співвідношення.

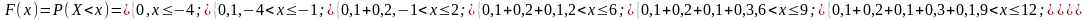
Щільність розподілу ймовірностей та її властивості

Для неперервних випадкових величин закон розподілу ймовірностей зручно описувати з допомогою щільності ймовірностей, яку позначають f(x).

Щільністю ймовірностей неперервної випадкової величини Х називається перша похідна від інтегральної функції F(x):

(3)

Властивості f(X)

1. f(x) ≥ 0. Ця властивості випливає з означення щільності ймовірності як першої похідної від F(x) за умови, що F(x) є не спадною функцією.

2. Умова нормування неперервної випадкової величини Х:

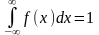
Якщо неперервна випадкова величина Х визначена лише на проміжку [a; b], то умова нормування має такий вигляд:

3. Можливістьсть попадання неперервної випадкової величини в інтервал [α; β], обчислюється за формулою

Залежність (4) можна подати так:

4. Якщо можливі значення неперервної випадкової величини належать лише інтервалу

[a; b], то

Закон розподілу ймовірностей як для дискретних, так і для неперервних випадкових величин дає повну інформацію про них. Проте на практиці немає потреби так докладно описувати ці величини, а достатньо знати лише певні параметри, що характеризують їх істотні ознаки. Ці параметри і називають числовими характеристиками випадкових величин.

Однією з найчастіше застосовуваних на практиці характеристик є математичне сподівання.

Математичним сподіванням дискретної випадкової величини Х, що приймає скінченну множину значень з законом розподілу

Р(Х = х_і) = р_к, к = 1, 2, … п (4)

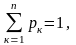(5)

називається сума добутків її значень на їх відповідні ймовірності:

(6)

Термін «математичне сподівання» випадкової величини Х є синонімом терміна «середнє значення» випадкової величини Х.

Якщо простір Ω є неперервним і всі значення Х належать проміжку

[а; b], а f(x) – її щільність ймовірностей, то

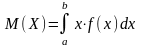(7)

Якщо випадкова величина Х 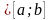, то М(Х) , а саме: математичне сподівання випадкової величини має обов’язково міститься в середині інтервалу [a;b], являючи собою центр розподілу цієї величини.