17. Корни натуральной степени.

Корень четной степени из отрицательного числа не определен!

1. 4. 7.

2. 5. 8.

3. 6.

Если a>b≥0, то и

Если a> 1,то >1 и .

Если 0<а< 1,то и .

18. Тригонометрия.

1. sin² x + cos² x = l. 3. . 5. .

2. . 4. . 6. .

Тангенс не определен для углов кратных 90°.

Котангенс не определен для углов кратных 180°.

Формулы сложения: 1. .

2. .

3. .

4. .

5. . 6. .

7. . 8. .

Формулы двойного аргумента: 1. .

2. . 3. . 4. .

5. . 3а) . 4а) .

6. .

Формулы суммы и разности тригонометрических функций:

1. 2.

3. 4.

5. 6.

7. 8.

Формулы половинного аргумента:

1. . 4. .

2. . 5. .

3. . 6. .

Формулы произведения тригонометрических функций:

1. . 3. .

2. . 4. .

5. . 6. . 7. .

Формулы тригонометрических функций через тангенс половинного аргумента:

. . . .

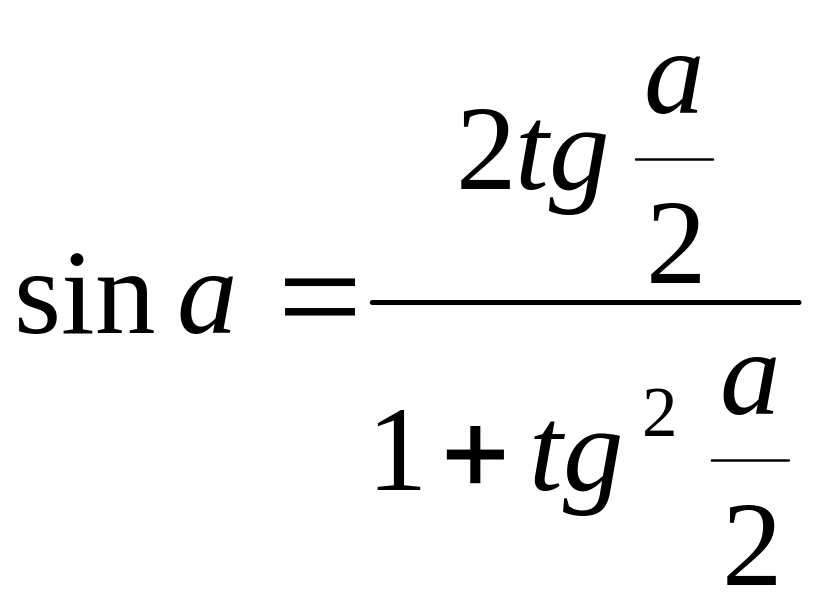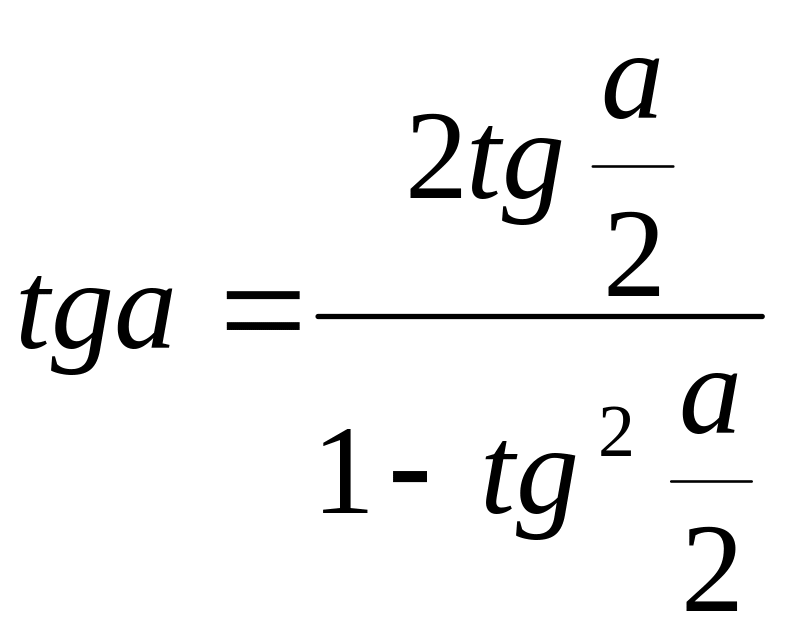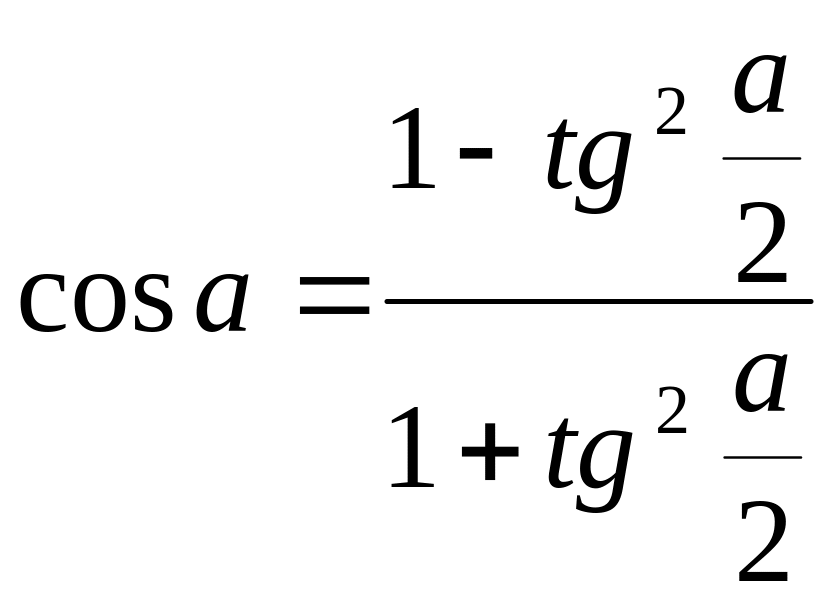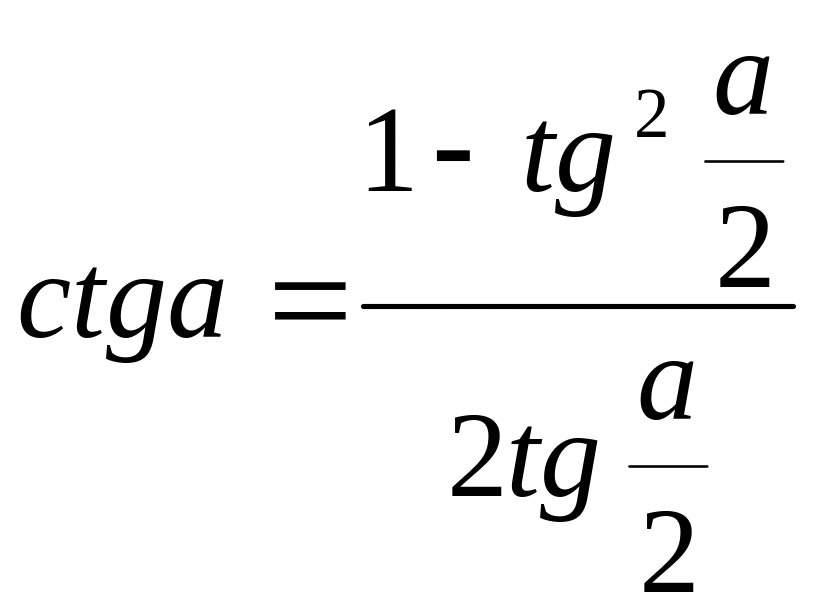19. Формулы сокращённого умножения.

1. (a + b)² = a²+2ab+b²; 4. (a + b)³ = a³+3a²b+3ab²+b³ ;

2. (a - b)² = a²-2ab+b²; 5. (a - b)³ = a³-3a²b+3ab²-b³ ;

3. a² – b² = (a-b)(a+b);

6. a³+b³= (a+b)(a²-ab+b² );

7. a³-b³ = (a-b)(a²+ab+b²).

20. Свойства степеней.

1. аⁿ = а∙ а∙...∙ а, n — натуральное число

n раз

2. а° = 1, (а 0, т.к. 0 ° - не определено)

3.

4. например,

5. , например

6. и

7. 10. (ab)ⁿ =aⁿ∙bⁿ

8. 11.

9.

Если a> b ≥ 0 и г > 0, то а^г >b^r.

Если а>b > 0 и г < 0, то а^r<b^r.

Если p > г и а > 1, то а^р > а^г.

Если р> г и 0 < а< 1, то а^р <а^г.

21. Квадратные уравнения.

ax²+bx+c = 0 (a 0) D = b² — 4ас - дискриминант квадратного уравнения.

D = b² - 4ас — дискриминант квадратного уравнения.

При а>0, D<0 парабола «висит» над осью Ох, т. е. нет корней (рис 1).

Если а>0, D=0 парабола касается сверху оси Ох, т.е. один корень (рис 2).

Если а>0, D>0, то парабола пересекает ось Ох в двух точках х₁ и х_2, т. е. и (рис 3).

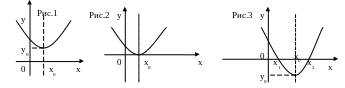
Аналогично при а<0.

ТЕОРЕМА ВИЕТА

Произведение корней приведенного квадратного уравнения равно свободному члену, а сумма корней равна второму коэффициенту, взятому с противоположным знаком, т.е.

x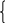 ²+px + q = 0, х₁+х₂= -р

x₁ и х₂ — корни х₁∙х₂=q

ТЕОРЕМА, ОБРАТНАЯ ТЕОРЕМЕ ВИЕТА

Если числа х₁ и х₂ таковы, что х₁ + х₂ = - р и х₁∙х₂= q, то они являются корнями уравнения

х² + рх + q = 0.

Пример. Решить уравнение х ² – 5х + 6 = 0.

Число 6 можно разложить на целые множители: 2 и 3, -2 и -3, а также 6 и 1, - 6 и - 1. Сумма корней должна давать второй коэффициент, взятый с противоположным знаком, т.е. 5. Подходят числа 2 и 3.

Ответ: х₁ =2,х₂ = 3.

КВАДРАТНЫЙ ТРЕХЧЛЕН

ах² + bх + с = а(х – x₁)(x – x₂) - разложение на множители, где х₁, х₂- корни;

если D = 0, т.е. один корень или два равных между собой, то ах² + bх + с = а(х - х₀)², где .