12. Параллельные прямые.

Две прямые называются параллельными, если они не пересекаются

Теорема. Две прямые, параллельные третьей, параллельны.

с

1 и 2; 3 и 4 — накрест лежащие углы

1 и 4; 2 и 3 — внутренние односторонние углы 1 и 5, 2 и 8, 3 и 6, 4 и 7 — соответственные углы

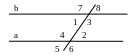
Признаки параллельности прямых:

Если внутренние накрест лежащие углы равны или сумма внутренних односторонних углов равна 180⁰ или соответственные углы равны, то прямые параллельные.

13. Углы.

Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми. ( 1 и 2)

Теорема. Сумма смежных углов равна 180⁰. ( 1+ 2=180⁰)

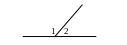
Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого угла.( 1 и 2, 3 и 4)

Теорема. Вертикальные углы равны. ( 1= 2, 3= 4)

14. Векторы и координаты.

1. А(х₁; у₁), В(х_2; у₂) - две точки на плоскости

2. М - координаты середины отрезка

3. AB= - длина отрезка

4. - координаты вектора .

5. Равными называются векторы, которые равны по длине и совпадают по направлению.

6. Равные векторы имеют равные соответствующие координаты и обратно:

7. — вектор

8. | | = - длина (абсолютная величина) вектора

9. - скалярное произведение векторов, выраженное через координаты векторов и .

10. - скалярное произведение векторов, выраженное через длины векторов и угол между ними.

11. cosα = , — косинус угла между векторами

12. - критерий перпендикулярности векторов

13. ║ - критерий коллинеарности векторов

14. ах + bу = с - уравнение прямой, k = — угловой коэффициент прямой

15. (х-а)² +(у-b)² =R² - уравнение окружности с центром в точке O(a;b) и радиусом R

16. х² +у² =R² - уравнение окружности с центром в начале координат.

15. Формулы площади.

Треугольники: - половина произведения основания на высоту

- половина произведения двух сторон на синус угла между ними

- формула Герона, где .

площадь правильного (равностороннего) треугольника

, где —катеты —площадь прямоугольного треугольника

через радиус описанной окружности

S=pr, где - через радиус вписанной окружности

Четырехугольники: S = ab - площадь прямоугольника

S=a² – площадь квадрата

S = ah_а = absin α - площадь параллелограмма

S = mh - площадь трапеции

, S = ah_а = a²sin α — площадь ромба.

, - площадь четырехугольника (выпуклого)

Многоугольник: , где Р — периметр, а r — радиус вписанной окружности

Площади подобных треугольников (фигур) относятся как квадраты их сходственных сторон (элементов) .

16. Свойства корней.

Квадратные корни

1. Для = b имеем . 4. , (а≥0, b≥0).

2. , (а≥0) 5.

3. =|а| (а-любое) 6. (а ≥ 0)

Вынесение из-под корня , b≥0.

если a<0

Внесение под корень если a>0