10. Окружность.

1. Окружностью называется фигура, состоящая из всех точек плоскости, равноудаленных от данной точки. Эта точка — центр окружности (точка О). Расстояние от точек плоскости до ее центра называется радиусом ( R=AO=DO). Отрезок, соединяющий две точки окружности, называется хордой (BC). Хорда, проходящая через центр называется диаметром (d=AD, d=2R).

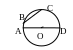
2. Центр окружности, описанной вокруг треугольника, лежит на пересечении серединных перпендикуляров к сторонам треугольника

3. радиус описанной окружности для треугольника

4. радиус описанной окружности для треугольника (из теоремы синусов).

5. Центр вписанной окружности лежит на пересечении биссектрис треугольника.

6. — радиус вписанной окружности для треугольника (многоугольника — где р — полупериметр ).

7. 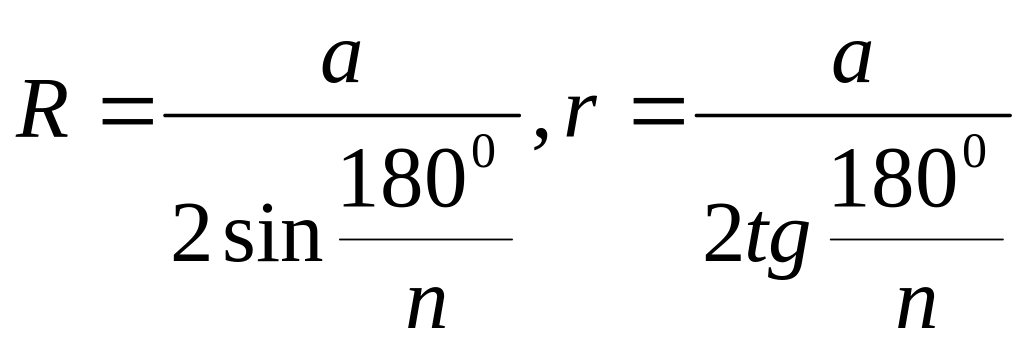— радиус описанной и радиус вписанной окружности (для правильного многоугольника).

8. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла (Рис 8).

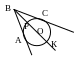
9. Отрезки касательных, проведенных из одной точки к окружности, равны между

собой АВ=ВС (Рис 8).

Рис 8

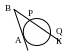
10. Квадрат отрезка касательной равен произведению секущей на ее внешнюю часть: АВ² = BP∙BQ (Рис 9).

Рис 9

11. Вписанный угол равен половине соответствующего центрального угла и равен половине градусной меры дуги, на которую он опирается, т. е. (Рис 10)

12. Угол между касательной и секущей, проходящими через одну точку окружности, равен половине градусной меры дуги, заключенной внутри угла или ( Рис 11).

Рис 10

Рис 12

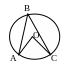
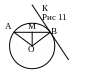
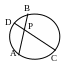
12. Произведения отрезков пересекающихся хорд равны между собой, т.е. AP∙BP=CP∙DP. (Рис. 12)

13. Свойство описанного четырехугольника:

В описанном четырехугольнике суммы противоположных сторон равны: AB+CD=BC+AD (Рис 13).

14. Признак описанного четырехугольника:

Если у четырехугольника суммы противоположных сторон равны, то в него можно вписать окружность (Рис 13).

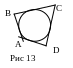
15. Свойство вписанного четырехугольника:

Во вписанном четырехугольнике сумма противоположных углов равна 180° (Рис 14).

16. Признак вписанного четырехугольника:

Если у четырехугольника сумма двух противоположных углов равна 180°, то вокруг него можно описать окружность (Рис 14).

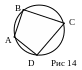
17. , - длина окружности, S = - площадь круга.

18. —длина дуги, - площадь сектора, .

19. Прямая, проходящая через точку окружности перпендикулярно к радиусу, проведенному в эту точку, называется касательной.

(а АО, а— касательная, АО — радиус)

11. Теорема Фалеса.

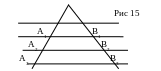
1. Если на одной стороне угла отложить равные отрезки и через их концы провести параллельные прямые, то на другой стороне угла отложатся равные между собой отрезки.

Если А₁А₂=А₂А₃ и А₁В₁║А₂В₂║А₃В₃, то В₁В₂=В₂В₃ (Рис 15).

2. Теорема, обратная теореме Фалеса:

Если на сторонах угла от его вершины отложить равные (пропорциональные) отрезки, то прямые соединяющие их соответствующие концы будут параллельны

Теорема Фалеса позволяет обосновать деление отрезка на несколько равных частей и на пропорциональные части.

3. Теорема о пропорциональных отрезках: Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла равные отрезки.