2. Приклад аналізу точності лінійної системи при випадкових впливах

Визначити дисперсію результуючої помилки після закінчення перехідного процесу в системі, структурна схема якої приведена на рис 2.1., для таких параметрів:

; ; ;

; ; ; ; .

1. Визначимо передаточну функцію по помилці для корисного повідомлення:

.

2. Знайдемо дисперсію помилки, викликану корисною дією з заданим енергетичним спектром :

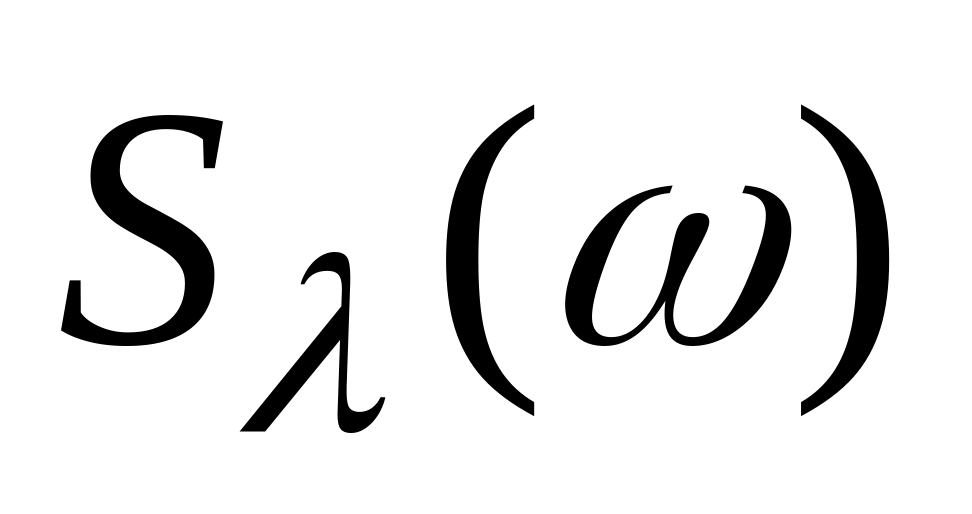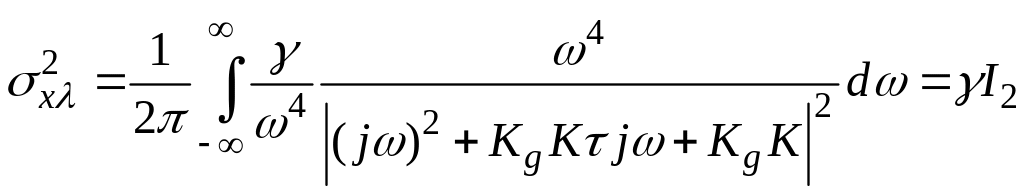
Звідси для знаходимо ; ; ; ; .

Тоді

.

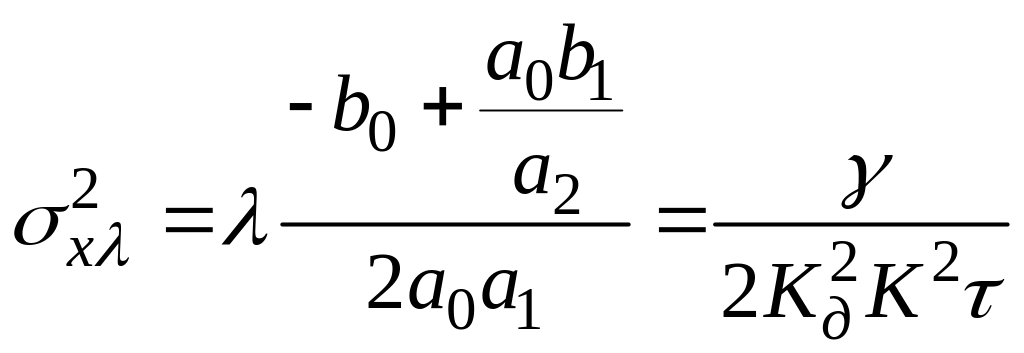3. Визначимо передаточну функцію по помилці для заважаючого впливу :

.

4. Обчислимо дисперсію помилки, обумовлену заважаючим впливом:

.

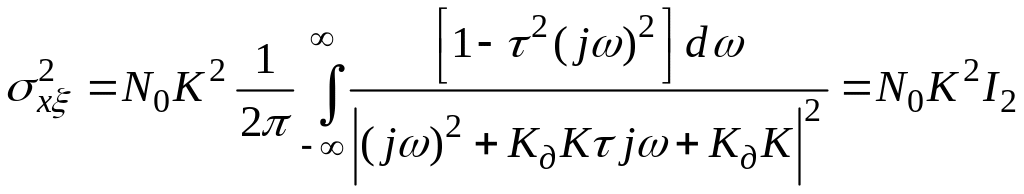При отримаємо ; ; ; ; ,

.

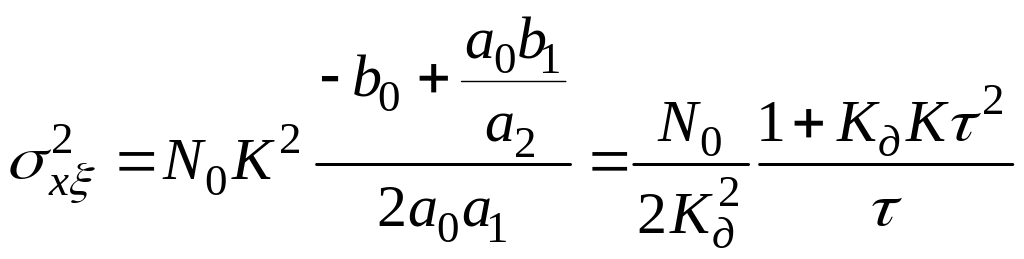5. Обчислимо дисперсію результуючої помилки:

.

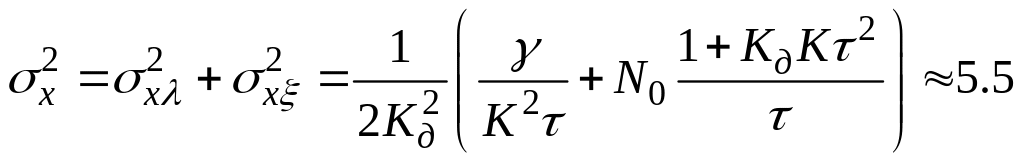3. Оптимізація параметрів слідкуючих систем

Задачі оптимізації параметрів радіотехнічних слідкуючих систем дуже різноманітні. Вони відрізняються не тільки структурою даних систем, але і видом впливів, що діють на систему, критеріями, по яких ведеться оптимізація, наявністю додаткових вимог і обмежень.

Найбільш характерні для слідкуючих систем такі випадки.

1. Корисні і заважаючі впливи є детермінованими процесами. При цьому як критерій оптимізації використовується мінімум сумарної помилки

.

2. Корисне повідомлення описується регулярною функцією, а заважаючий вплив - флюктуаційний процес. Критерієм оптимізації є мінімум сталого значення середнього квадрата помилки:

.

3. Дії і є випадковими процесами. Тоді мінімізації підлягає дисперсія результуючої помилки:

.

Вважаючи, що результуюча помилка (дисперсія, середній квадрат) описується функцією , завдання оптимізації можна звести до вигляду

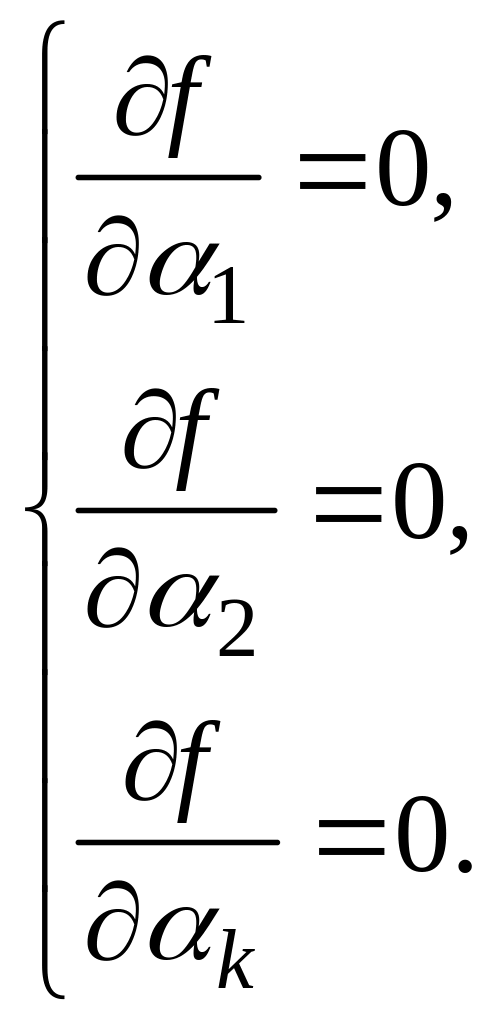
Вирішуючи спільно систему рівнянь, знаходимо оптимальні значення параметрів .

У якості ілюстрації визначимо оптимальні значення коефіцієнта підсилення і постійної часу системи, розглянутої в прикладі 2.2.2.

Як було показано, дисперсія результуючої помилки

.

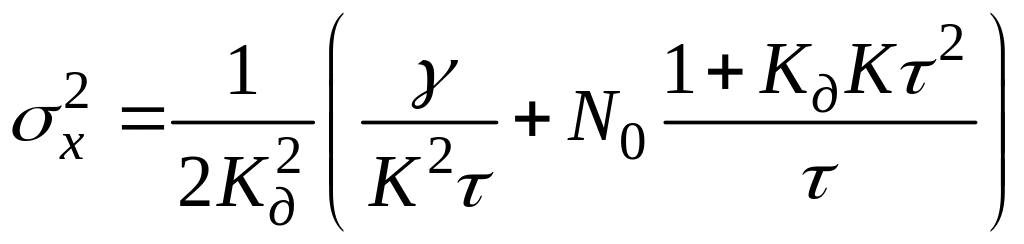Звідси для знайдення найкращих (у сенсі мінімуму ) значень і обчислимо відповідні частні похідні і прирівняємо їх до нуля:

;

.

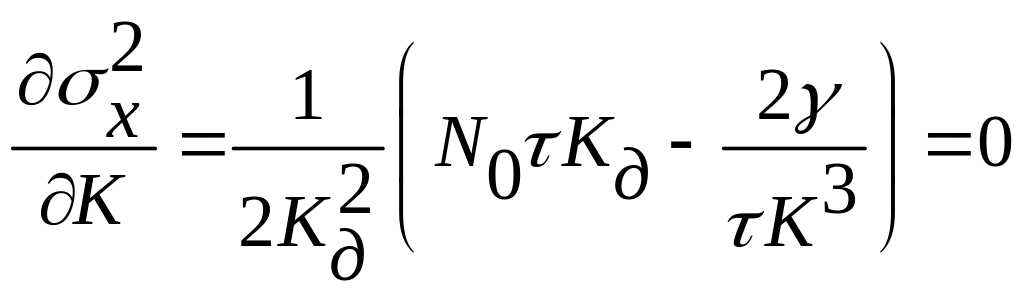Спільно вирішуючи рівняння, отримуємо

.

4. Аналіз лінійних систем методом простору станів

Розглянемо систему радіоавтоматики, що описується диференційним рівнянням вигляду

(2.10)

Послідовною заміною змінних можна здійснити перехід від скалярного диференційного рівняння n- го порядку (2.10) до векторного диференційного рівняння першого порядку (рівняння стану) [1;2]:

, (2.11)

де

- вектор (змінна) стану системи;

; .

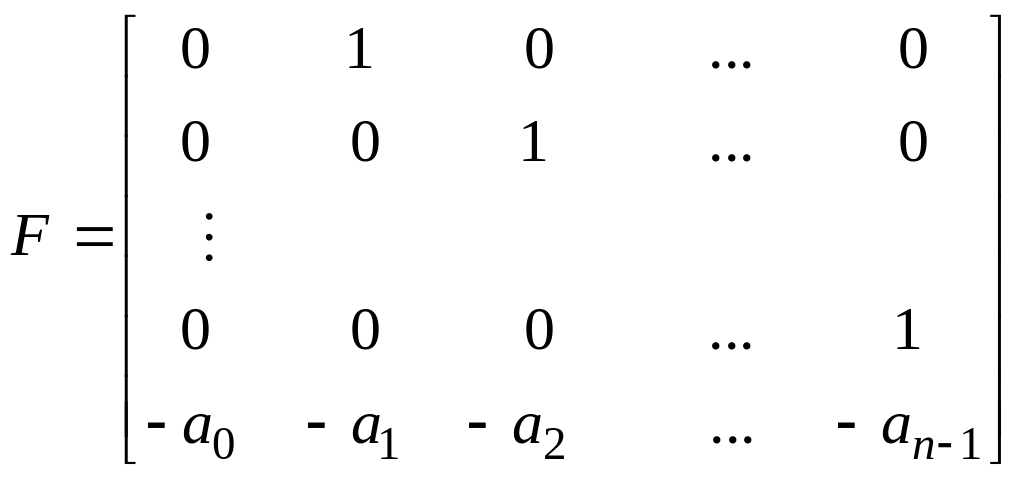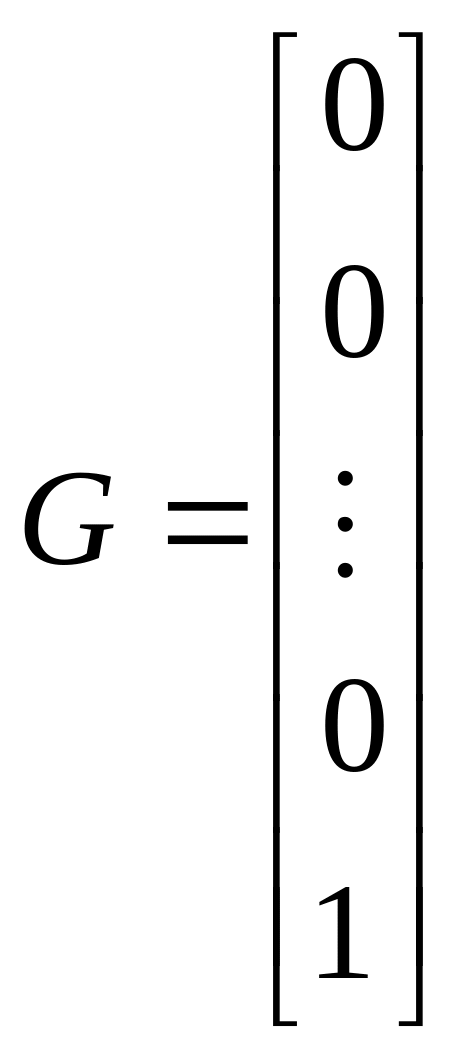Рівняння для вихідного сигналу (вихідне рівняння) можна записати у вигляді , де

. (2.12)

Загальне рішення векторного рівняння (2.11) дорівнює сумі загального рішення однорідного і частного рішення неоднорідного рівняння [1;2]:

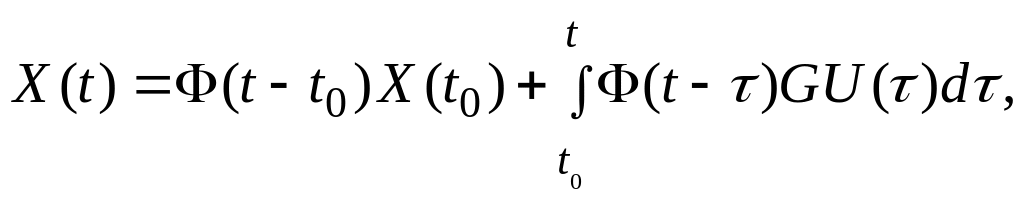(2.13)

де - перехідна матриця системи;

- обратне перетворення Лапласа;

- одинична матриця.