4 Аналіз нелінійних систем радіоавтоматики

Багато систем автоматичного регулювання не можуть бути з достатньою точністю, а іноді навіть якісно правильно описані лінійними диференціальними рівняннями з постійними коефіцієнтами. Наприклад, неможливо за допомогою лінійних методів досліджувати системи, що працюють в коливальному або релаксаційному режимі, врахувати вплив обмеження, люфтів, насичення і багатьох інших явищ, що мають місце в реальних системах.

Системи, поведінка яких описується нелінійними диференціальними рівняннями, називаються нелінійними системами автомати­чного управління. З математичної точки зору найбільш значна відмінність лінійних систем від нелінійних полягає в тому, що до них не застосовний принцип суперпозиції, на якому заснований аналіз лінійних систем. Тому для дослідження нелінійних систем при де­термінованих впливах застосовують такі наближені ме­тоди: безпосередньої лінеаризації, кусочно-лінійної апроксима­ціі, фазової площини, гармонійного балансу, малого параметра і моделювання на ЕОМ.

Для аналізу нелінійних систем при випадкових впливах застосовуются найчастіше два методи: метод, заснований на теорії марківських випадкових процесів, і метод статистичної лінеаризації.

Далі розглянуті два методи аналізу нелінійних систем радіоавтоматики: метод гармонічної лінеарізації та метод статистичної лінеарізації.

4.1. Метод гармонічної лінеаризації (гармонічного балансу).

Метод гармонічної лінеаризації призначений для дослідження умов виникнення автоколивань і визначення амплітуди і час­тоти автоколивань в нелінійних системах.

Хай замкнута система складається з послідовно включених нелінійної безінерційної ланки НЛ і лінійної інерційної частині ЛЧ (рис.4.1).

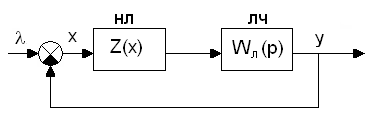
Рис. 4.1

У разі впливу на вхід НЛ гармонічного синусоїдального сиг­налу на його виході міститься спектр гармонічних складових з амплітудами , ,… і частотами , 2 , … . Передбачається, що сигнал , проходячи через лінійну частину , фільтрується нею в такому ступені, що в сигналі на виході лінійної частини можна нехтувати всіма вищими гармоніками , , … і вважати

.

Останнє припущення носить назву гіпотези фільтру і є необхідною умовою гармонічної лінеаризації [4] .

Для справедливості гіпотези фільтру необхідна така характе­ристика лінійної частини щоб, проходячи через неї, всі гармоніки, окрім першої, затухали до малих значень, якими можна нехтувати . Математично цю умову можна виразити співвідношенням

,

де =2, 3, … - номер гармоніки.

Звертаючись до структурної схеми, помічаємо, оскільки автоколивання мають місце при , то , а при виконанні гіпотези фільтру це означає: ; .

Нелінійна ланка при дії на її вхід гармонійного сигна­ла може бути описана (у припущенні справедливості гіпотези фільтру) комплексним коефіцієнтом підсилення, рівним відношенню комп­лексної амплітуди першої гармоніки вихідного сигналу до комплексної амплітуди вхідного гармонічного сигналу.

Розглянемо безінерційну нелінійну ланку з характеристикою . Якщо на вхід нелінійної ланки діє гармонічний сигнал , то періодичний сигнал на виході НЛ можна представити у вигляді ряду Фурье:

,

де

;

.

Вважаючи, що гіпотеза фільтру виконується і періоди­чний сигнал при гармонічній лінеаризації приблизно представ­ляється своєю першою гармонікою:

,

де

;

.

Звідси комплексний коефіцієнт підсилення нелінійної ланки:

;

; (4.1)

;

, .

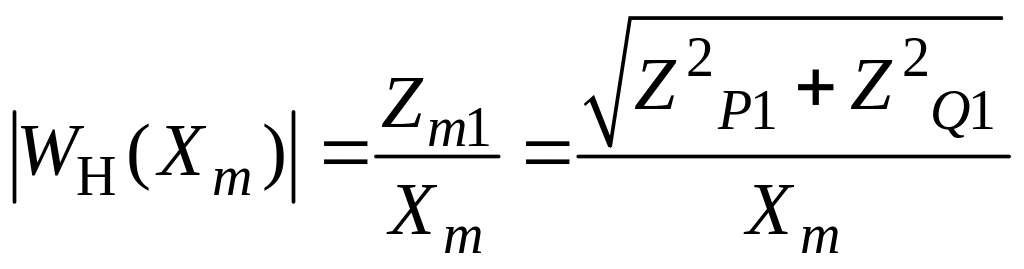Комплексний коефіцієнт підсилення показує співвідноше­ння амплітуд і фаз першої гармоніки вихідного і вхідного сигналів і в цьому сенсі нагадує комплексний коефіцієнт передачі лінійної ланки . Проте у разі НЛ залежить він не від частоти, а від амплітуди вхідного гармонічного сигналу .

Показано, що гармонічний сигнал зазнає фазового зсуву при проходженні через нелінійну ланку тільки у разі неоднознач­ної нелінійності, наприклад типу гістерезисної характеристики. При­чому уявна складова комплексного коефіцієнта підсилення [3; 4] :

, (4.2)

де - площа неоднозначної нелінійної характеристики. Для однозначної нелінійності .

Скориставшись комплексним коефіцієнтом підсилення НЛ, рівняння гармонічного балансу та , можна представити у вигляді

. (4.3)

Записавши окремо реальну і уявну частини цього рівняння

отримаємо систему рівнянь, що дозволяє визначити амплітуду і частоту можливих коливань в нелінійній системі.

Зручним способом вирішення рівняння (4.3) є запропонований Л.С.Гольдфарбом графічний метод. Перепишемо вираз (4.1) у вигляді

, (4.4)

де - інверсний комплексний коефіцієнт підсилення НЛ.

На комплексній площині побудуємо графіки лівої і правої частин рівняння (4.4) (рис.4.2). В точках перетину цих годографів виконується умова гармонійного балансу. Визначимо точку стійких коливань.

Нехай зона, яка лежить праворуч від годографа лінійної частини по ходу збільшення частоти, ек­вівалентна наявності коренів з додатною реальною частиною, а ліворуч - з від’ємною.

Розглянемо точку 1 перетину годографів і .

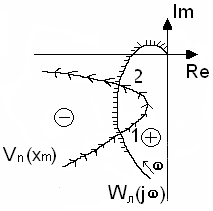
Рис.4.2.

Припустимо, що з якоїсь причини амплітуда авто­коливань збільшилася і ми перемістилися по годографу у бік зростання . При цьому з точки 1 переходимо в область , що еквівалентно наявності кореня з додатною дійсною частиною, а це приводить до збільшення амплітуди і порушення стійкості коливань. Якщо припустимо, що амплітуда автоколивань зменшилася, то ми пере­міщаємося по годографу в область, що відповідає наявності кореня з від’ємною дійсною частиною, де всі коливання повинні затухати і, отже, амплітуда повинна зменшуватися. Це дозволяє зробити висновок про нестійкість автоколивань в точці 1. Проводячи аналогічні міркування, можна прийти до висновку про стийкість автоколивань в точці 2.

Точці 2 годографа відповідає певна амплітуда першої гармоніки, але ця точка належить також годогра­фу , тому їй відповідає певна час­тота автоколивань. Таким чином, по годографу можна визначити амплітуду, а по годографу - частоту автоколивань в нелінійній системі.