1.4. Интервальное оценивание

Рассмотренные в разделе 1.2 статистические и оценочные характеристики М^*(x), D^*(x) и D(x) называются точечными, так как они характеризуют изучаемое явление одним числом. При небольшом числе испытаний указанные точечные характери­стики, как правило, отличаются от истинных значений математи­ческого ожидания и дисперсии. Иначе говоря, наблюдается раз­брос указанных характеристик. В связи с этим, в математической статистике наряду с точечными характеристиками применяются интервальные оценки - доверительный интервал и доверительная вероятность, которые дают представление о точ­ности и надежности точечных характеристик. Доверительный интервал характеризует точность, а доверительная вероятность характеризует надежность оценки.

Рассмотрим вопрос о нахождение доверительного интервала для математического ожидания с заданной надежностью γ. Пусть при выборочном обследовании по N измерениям было получено статистическое среднее арифметическое M^*(x). Требуется определить точность оценки, т.е. на какую величину Δ среднее значение измеряемого параметра в генеральной сово­купности М(х) отличается от статистического среднего арифме­тического M^*(x). Величина Δ называется точностью оценки, а интервал (M^*(x) - Δ; M^*(x) + Δ) - доверительным интервалом. Доверительная вероятность (надежность)

γ = Р(М^*(х) - Δ < М(х) < М*(х) + Δ) = Р(|М*(х) - М(х) < Δ). (1.13)

Если генеральная совокупность подчиняется нормальному закону распределению и объем выборки достаточно велик (N>25), то используется следующая формула;

Р(|М*(х) - М(х) < Δ) =2Ф , (1.14)

где Ф (х) - функция Лапласа (табл. 1 приложения);

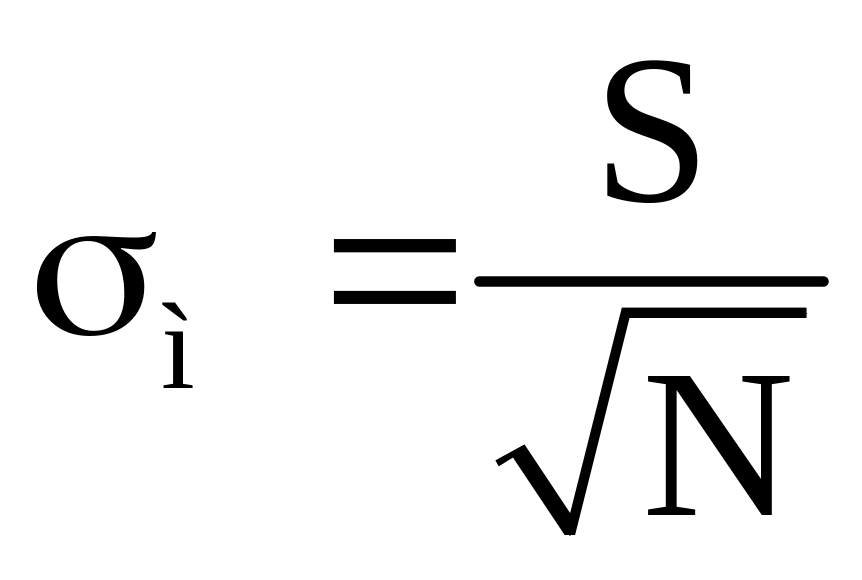- среднее квадратическое отклонение величины М*(Х);

Р - стандартное отклонение случайной величины.

Обозначим 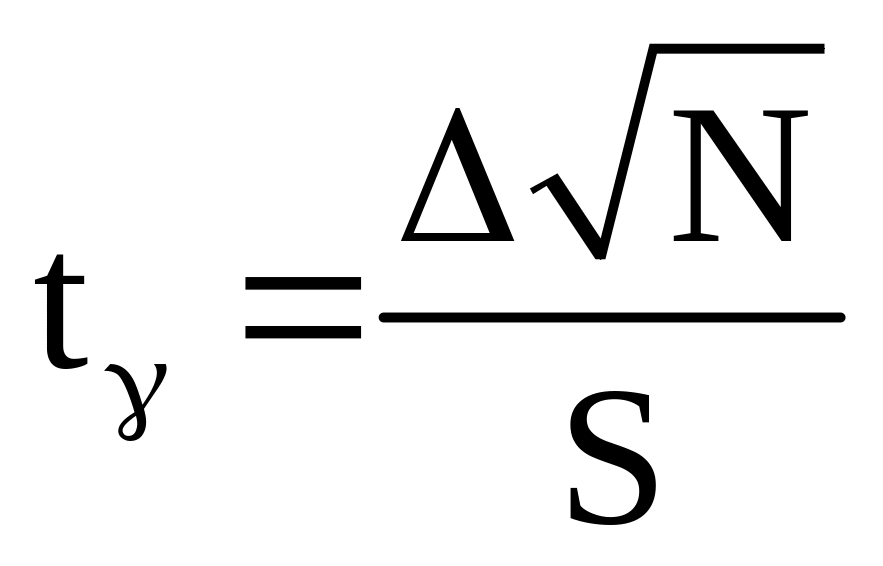, тогда

.

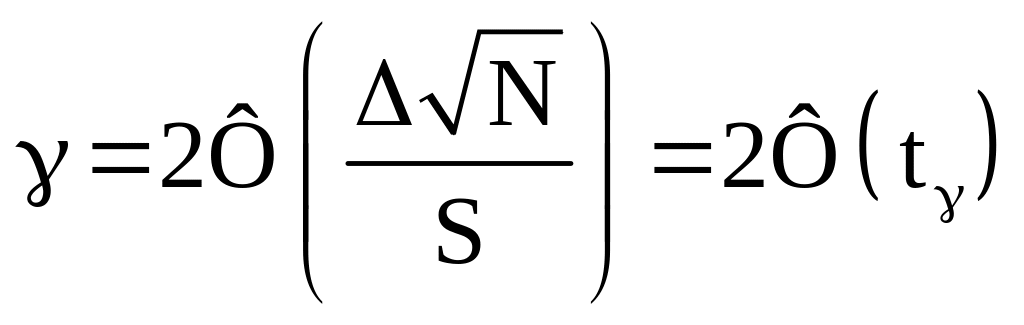По таблице 1 приложения значений функции Лапласа определяем число α, соответствующее заданной надежности γ, и нахо­дим точность оценки Δ по формуле

.

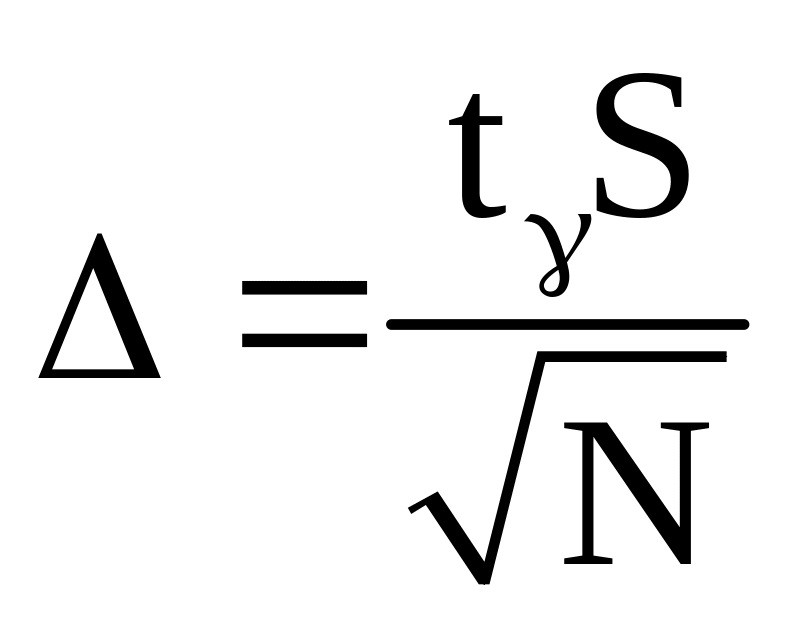В случае малых выборок (N < 25) пользуются соотношением

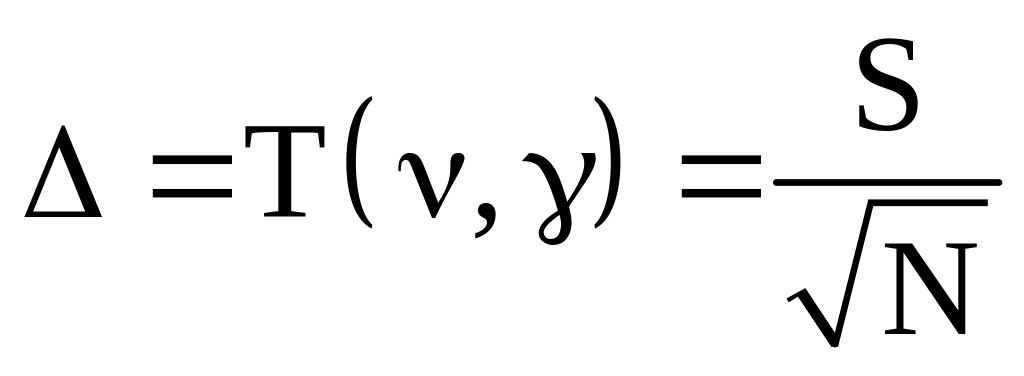. (1.17)

где - коэффициент доверия для заданного числа степеней ν = N - 1 и доверительной вероятности γ.

Значения приведены в таблице II приложения.

На основании проведенного анализа можно сделать следую­щие выводы:

при возрастании объема выборки N число Δ убывает и, следовательно, точность оценки возрастает;

увеличение надежности оценки γ приводит к увеличению t_γ или и, следовательно, к возрастанию Δ, что ведет за собой уменьшение точности оценки;

минимальный объем выборки, который обеспечивает оценку истинного математического ожидания М(x) с заданной надеж­ностью γ и точностью Δ, определяется по формуле

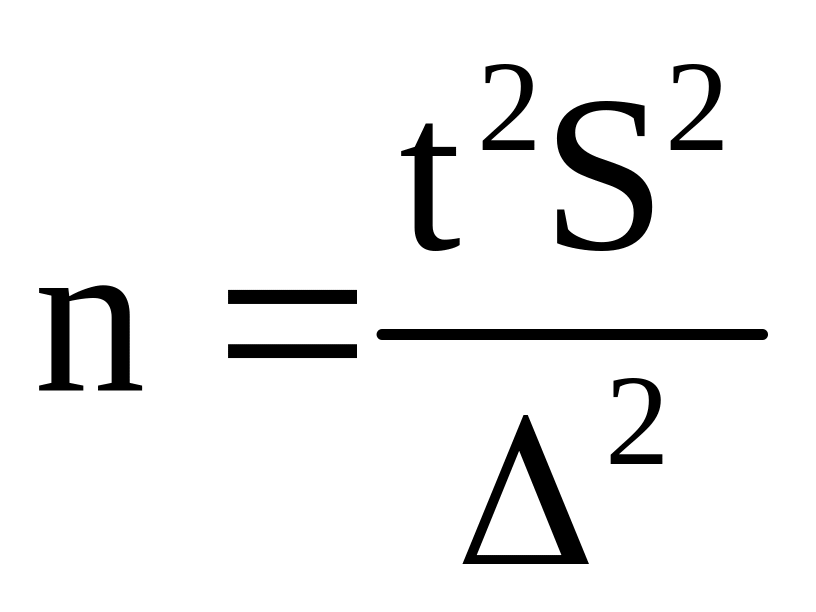. (1.18)

В заключении для рассматриваемого примера (см. табл. 1.2) покажем порядок определения доверительного интервала разброса среднего результата (истинного математического ожидания).

1. Вычисляем статистическое среднее арифметическое

2. Вычисляем статистическую дисперсию

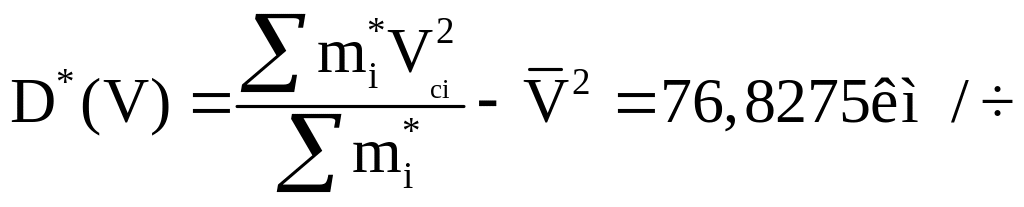
3. Вычисляем несмещенное значение дисперсии и несмещенное значение среднего квадратического отклонения

.

4. Находим среднее квадратическое отклонение среднего результата

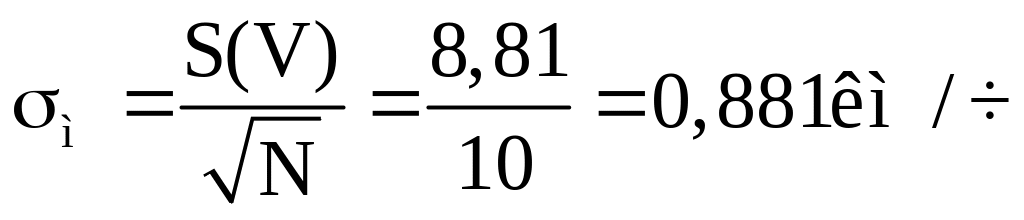
5. Так как объем выборки N = 100 > 25 велик, то для заданной надежности γ=0,95 величина

.

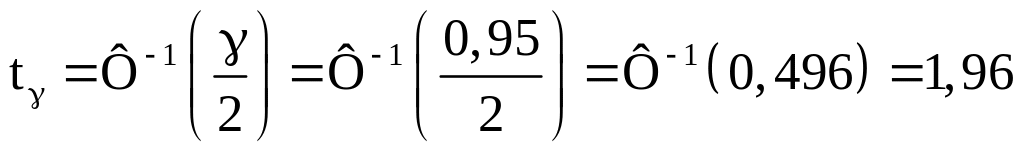Ф^-1(х) - обращенное значение функции Лапласа.

6. Находим точность оценки

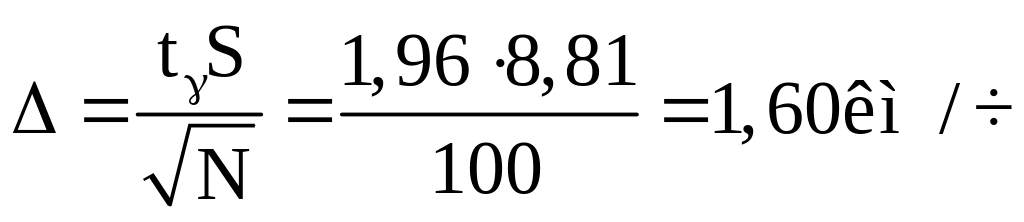
7. Находим доверительный интервал для математического ожидания

М^*(х) - Δ < М(х) < М*(х) + Δ= (44,35 - 1,60 < М(х) < 44,35+1,60) = (42,75 < М (x) < 45,95),

Следовательно, с надежностью γ = 0,95, можно утверждать, что значение математического ожидания генеральной совокупно­сти находится в пределах (42,75; 45,95).

Итак, в первой главе изучены вопросы сбора информации, группировки исходных данных, построения гистограммы, полигона и кумулятивной кривой, рассмотрен порядок и методология оце­нивания точечных статистических характеристик случайных вели­чин, сделана интервальная оценка математического ожидания. На базе выполненного анализа можно приступать к следующему этапу статистической обработки - выравниванию эксперименталь­ных данных различными законами распределения.