2.8. Статистическая проверка гипотезы о принадлежности опытных данных к гамма-распределению

Гамма-распределение наряду с другими законами находит самое широкое применение при исследовании различных явлений. Так данное распределение применяется при описании безотказ­ной работы системы, выходящей из строя после m независимых её отказов, при определении распределения времени между двумя последовательными операциями по обслуживанию систем и т.д. Гамма-распределение представляет собой композицию нескольких показательных законов.

Плотность гамма-распределения имеет вид:

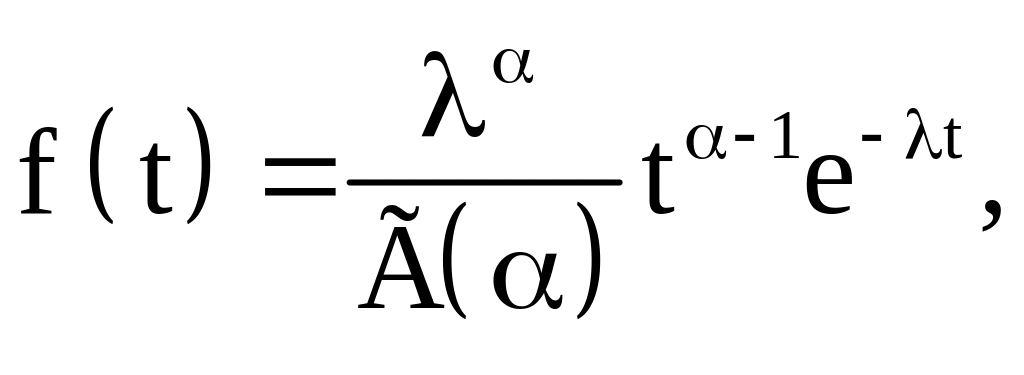
где Г(α) = (α - 1)! - гамма-функция Эйлера;

t - случайная величина;

α - параметр, численно равный числу складываемых законов;

λ - параметр, численно равный интенсивности числа появлений отказов каждого из складываемых показа­тельных законов.

График плотности гамма-распределения для различных зна­чений α и λ показан на рис. 2.9.

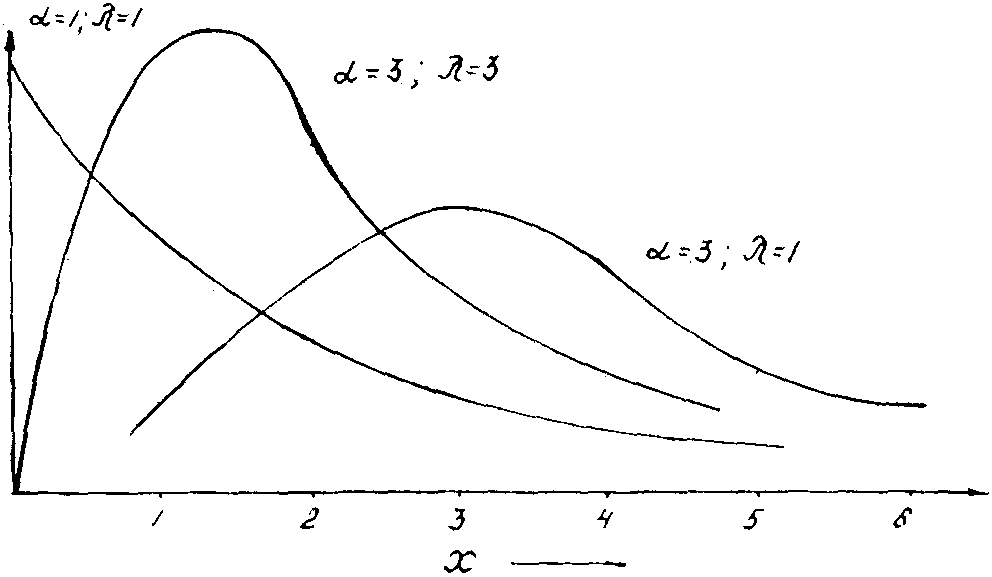
Рис. 2.9. График плотности гамма-распределения

Частными случаями гамма-распределения являются:

показательное распределение при α = 1;

распределение Эрланга, широко применяемое в теории массового обслуживания, возникающее при α целом положительном;

распределение χ² (хи - квадрат), при λ = 0,5 и α, крат­ном 0,5,

При некоторых значениях параметров при λ и α гамма-распределе­ние приближается к закону Вейбулла. По мере увеличения пара­метра α гамма-распределение преобразуется в нормальный закон

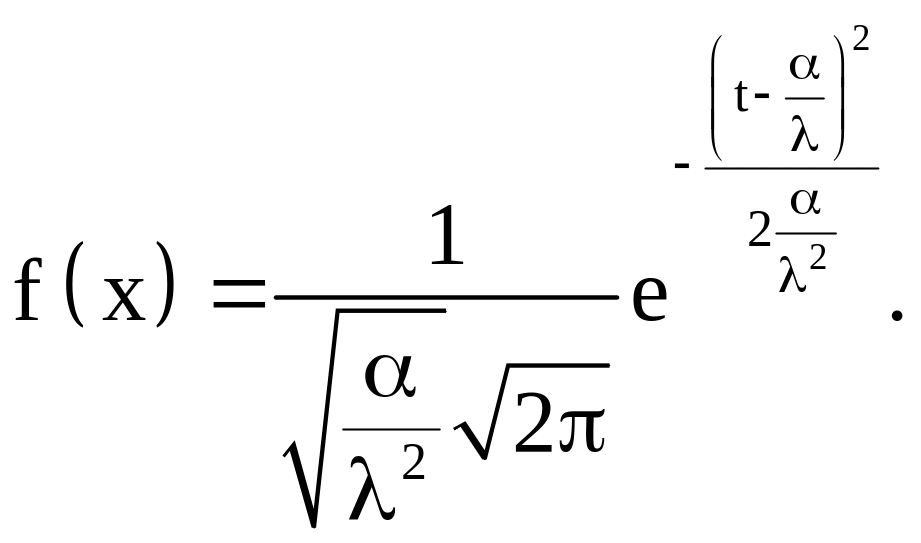(2.25)

Математическое ожидание и дисперсия гамма-распределения через параметры α и λ выражаются следующими зависимостями:

(2.26)

Покажем на примере порядок проверки гипотезы о принадлежности опытных данных к гамма-распределению. Исследуется один из этапов транспортного, процесса - время продолжительности пог­рузки автомобилей на комбинате силикатно-строительных матери­алов. Всего было зафиксировано 80 наблюдений. Максимальное время продолжительности погрузки составило 106 мин, мини­мальное - 10 мин.

1. С помощью формулы Стерджеса определяем приближенную ширину интервала

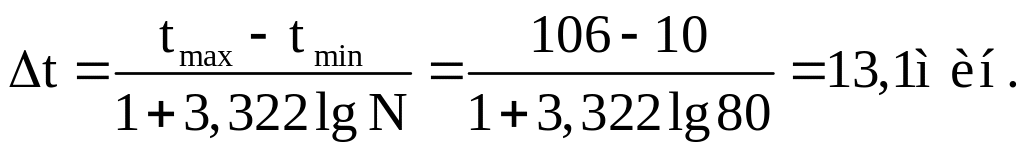
За величину ширины интервала принимаем Δt = 12 мин. Тогда гисто­грамма будет иметь 9 интервалов.

2. На основании методики, изложенной в 1.2, определяем статистические поинтервальные частоты и частости попадания слу­чайной величины в интервалы. На основании полученных данных строим гистограмму распределения (рис.2.10). Все результаты расчетов заносим в табл. 2.10.

3. Используя данные расчетов в столбцах 6 и 7 табл. 2.10, находим статистические математическое ожидание и дисперсию

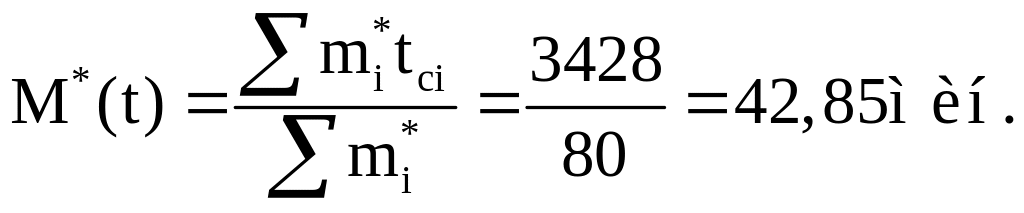
Находим несмещенную оценку для среднего квадратического отклонения

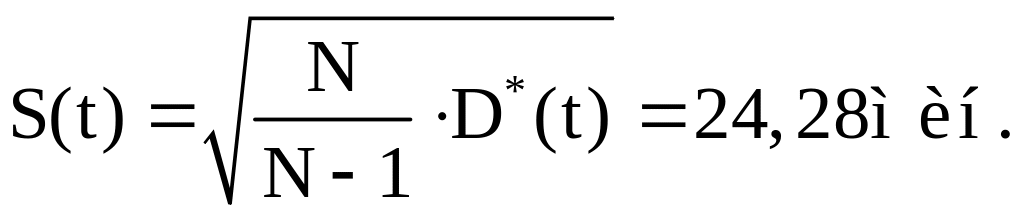
4. Определяем параметры гамма-распределения, для него решаем систему уравнений (2.26)

Получаем α = 3,153; λ = 0,0736,

5. Находим вероятности попадания случайной величины, описываемой гамма-распределением, в интервалы.

Так как гамма-распределение является двухпараметрическим законом, то её плотность-распределение преобразуют к более удобному виду. Дня этого делают замену переменных, полагая

(2.27)

Номер разряда	Границы интерва­лов времени простоя αi - βi, мин	Середины интервалов tci, мин	Опыт­­ные часто­ты	Опыт­ные часто­сти			Теорети­ческие вероятно­сти Pi	Теорети­чес­кие числа попадания в интер­валы	Слагаемые критерия Пирсона
1	2	3	4	5	6	7	8	9	10
1	4-16	10	8	0,100	80	800	0,102	8,2	0,01
2	16-28	22	17	0,2175	374	8228	0,212	17,0	0
3	28-40	34	18	0,225	612	20808	0,219	17,5	0,01
4	40-52	46	13	0,1625	598	27508	0,173	13,9	0,06
5	52-64	58	10	0,125	580	33640	0,113	9,1	0,09
6	64-76	70	5	0,0625	350	24500	0,078	6,2	0,23
7	76-88	82	3	0,0375	245	20172	0,046	3,7	0,13
8	88-100	94	4	0,050	376	35344	0,024	1,9	2,32
9	I00-112	106	2	0,025	212	22472	0,012	1,0	1,00
Итоговая строка			=80	==1,0	=3428	=193472			χ2 = 3,85

После замены плотность гамма-распредехения принимает вид:

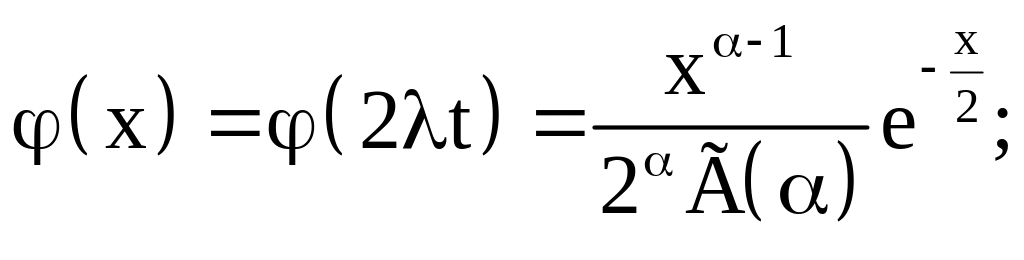
Функция φ(2λt) имеет важное преимущество перед функцией f(t) - она зависит только от одного параметра λ, в то время, когда функция f(t) зависит от двух параметров α и λ.

Значения функции φ(2λt) табулированы (табл. VIII приложения).

Пользуясь данными этой таблицы и методом линейной интер­поляции, вычисляем теоретические вероятности попадания слу­чайной величины в интервалы. Все промежуточные и конечные ре­зультаты расчетов удобно помещать во вспомогательную табл.2.11.

Таблица 2.11

t	2λt	φ(2λt)	f(t) = 2λφ(2λt)	Pi = f(t)Δt
10	1,472	0,058	0,00854	0,102
22	3,238	0,120	0,01766	0,212
34	5,005	0,124	0,01825	0,219
46	6,771	0,098	0,01443	0,173
58	8,538	0,064	0,00942	0,113
70	10,304	0,044	0,00648	0,078
82	12,070	0,026	0,00383	0,046
94	13,837	0,0135	0,00199	0,024
106	15,603	0,0065	0,00096	0,012

На основании данных столбца 8 табл.2.10 наносим на гистограмму распределения сглаживающую её теоретическую кривую гамма-распределения

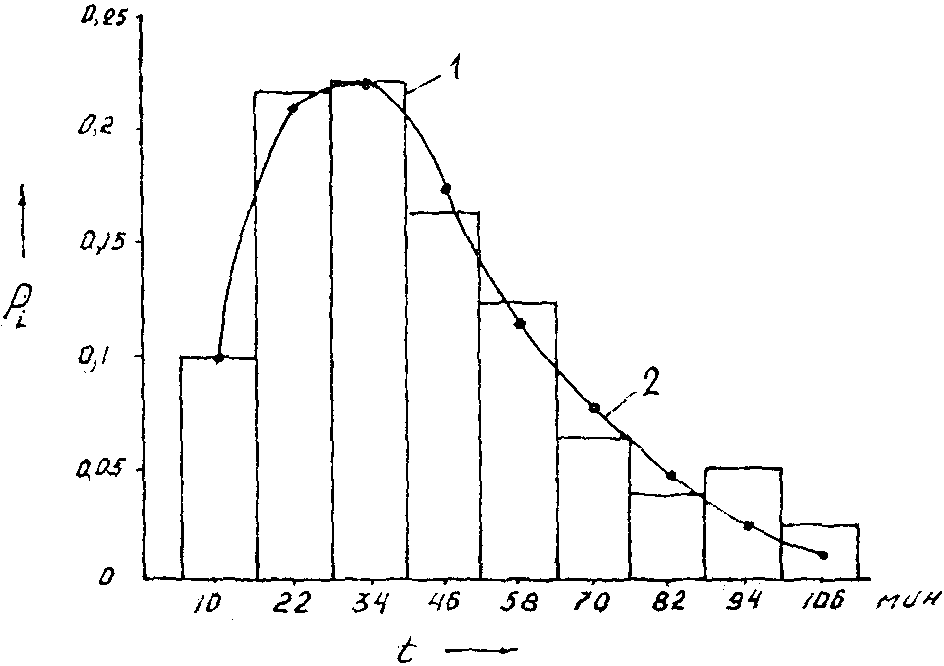
Рис.2.10. Гистограмма распределения времени продолжительности погрузки (1) и выравнивающая её теоретическая кривая гамма-распределения (2)

6. Вычисляем теоретические числа попадания случайной величины в интервалы. Результаты расчетов заносим в столбец 9 табл. 2.10.

7. Находим составляющие критерия Пирсона. Результаты вычислений помещаем в столбец 10 табл.2.10. При этом сумма значений составляет

8. Проверяем правдоподобность гипотезы о принадлежности опытных данных к гамма-распределению. Для рассматриваемого примера число степеней свободы К = n - S = 9 - 3 > 6 и заданный уровень значимости α = 0,05. По табл. V приложения с помощью линейной интерполяции находим

(χ²; К) = P(3,85; 6) = 0,696 > 0,05.

Следовательно, по критерию Пирсона гипотеза о принадлежности опытных данных к гамма-распределению подтверждается.

9. Проверяем правдоподобность принятой гипотезы с помощью критерия Романовского

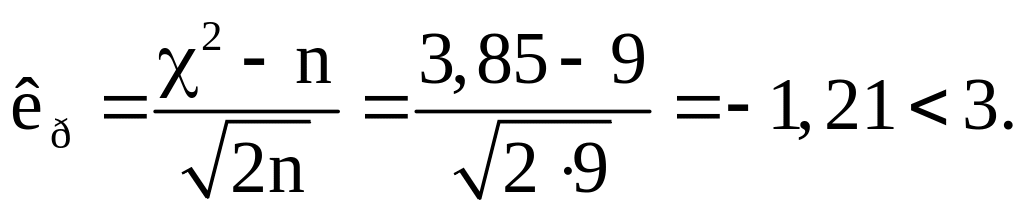
И по критерию Романовского гипотеза о принадлежности опытных данных к гамма-распределению не отвергается.

10. Найдем доверительный границы для разброса среднего ре­зультата с надежностью γ = 0,95.

Так как N = 80 > 25, то при γ = 0,95, t_γ = 1,96.

Определяем точность оценки

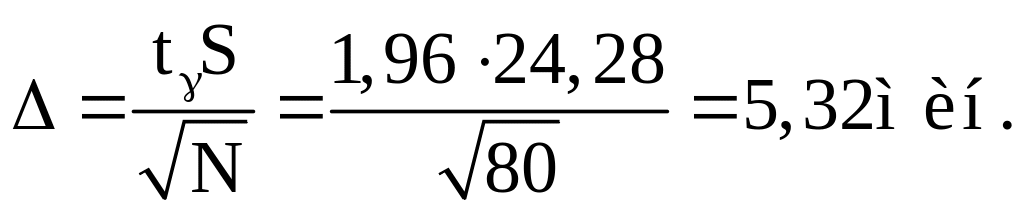
Следовательно, среднее время продолжительности погрузки находится в пределах

M*(t) - Δ < M(t) < M^*(t) + Δ;

42,85 - 5,32 < M(t) < 42,85 + 5,32, или

37,53 < M(t) < 48,17.

При организации транспортного процесса, как правило, учиты­вают верхнюю границу доверительного интервала t_max = 48,2 мин.