Функция мода

Синтаксис:

МОДА (число!; число2;...)

Результат:

Отображает наиболее часто встречающееся значение в интер­вале данных.

Аргументы:

число!, число2, ...: от 1 до 30 аргументов, для которых вычис­ляется мода.

Замечания:

• аргументы должны быть числами, именами, массивами или ссылками, которые содержат числа;

• если аргумент, который является массивом или ссылкой, со­держит текстовые, логические значения или пустые ячейки, то такие значения игнорируются, однако ячейки, содержащие нуле­вые значения, учитываются;

• если множество данных не содержит одинаковых данных, то функция МОДА помещает в ячейку значение ошибки #Н/Д.

Математика-статистическая интерпретация:

Модой (Мо) называется чаще всего встречающаяся варианта или то значение признака, которое соответствует максимальной точке теоретической кривой распределения.

Мода широко используется в коммерческой практике при изучении покупательского спроса (при определении «ходовых» размеров одежды и обуви, наиболее употребляемых продуктов и т. п.). В дискретном ряду мода - это варианта с наибольшей час­тотой.

В отличие от дискретного вариационного ряда определение моды по интервальному ряду требует проведения расчетов по фор­муле.

где: - нижняя граница модального интервала;

- величина модального интервала;

- частота модального интервала;

- частота интервала, предшествующего модальному:

- частота интервала, шествующего за модальным.

Функция СТАНДОТКПОН

См. также ДИСП, КВАДРОТКЛ, СРОТКЛ, СТАНДОТКЛОНА, СТАНДОТКЛОНП.

Синтаксис:

СТАНДОТКЛОН (число1; число2;...)

Результат:

Оценивает генеральное стандартное отклонение по выборке.

Аргументы:

число1, число2,...: от 1 до 30 аргументов, соответствующих вы­борке из генеральной совокупности.

Замечания:

• функция СТАНДОТКЛОН предполагает, что аргументы являются выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, то стан­дартное отклонение следует вычислять с помощью функции СТАНДОТКЛОНП;

• логические значения, такие, как ИСТИНА или ЛОЖЬ, а также текст игнорируются. Если текстовые и логические значе­ния игнорироваться не должны, следует использовать функцию СТАНДОТКЛОНА.

Математика-статистическая интерпретация:

В режиме «Описательная статистика» функция СТАНДОТКЛОН совместно с функцией СЧЕТ используется также для оп­ределения средней ошибки выборки выборки (показатель Стандартная ошибка в табл. 2).

Средняя ошибка выборки характеризует стандартное откло­нение вариантов выборочной средней от генеральной средней и зависит от вариации признака в генеральной совокупности, числа отобранных единиц, а также от способа организации выборки. Средняя ошибка повторной собственно-случайной выборки определяется по формуле:

Средняя ошибка выборки используется для расчета пре­дельной ошибки выборки (показатель Уровень надежности в табл. 2), которая дает возможность выяснить, в каких пределах находится величина генеральной средней. Предельная ошибка выборки связана со средней ошибкой выборки соотношением:

где t- коэффициент доверия, который определяется в зависимости от того, с какой доверительной вероятностью нужно гарантировать результаты выборочного обследования.

В Microsoft Excel коэффициент доверия t рассчитывается через функцию СТЬЮДРАСПОБР, в которой в ка­честве аргументов задаются уровень значимости  и число степе­ней свободы df. Уровень значимости а связан с доверительной вероятностью  (задается в поле Уровень надежности диалогового окна Описательная статистика) выражением  = 1 — . Число степеней свободы df зависит от объема выборки n и связано с ним выражением df = n — 1.

Функция ДИСП

ДИСП (число1; число2;...) Результат: Оценивает генеральную дисперсию по выборке.

Аргументы:

число1, число2,...: от 1 до 30 аргументов, соответствующих вы­борке из генеральной совокупности.

Замечания:

• функция ДИСП предполагает, что аргументы являются вы­боркой из генеральной совокупности. Если данные представляют всю генеральную совокупность, вычисляйте дисперсию, исполь­зуя функцию ДИСПР.

Математика-статистическая интерпретация:

В связи с тем, что изучаемые статистикой признаки варьиру­ются, обобщающие показатели в выборке могут в той или иной мере отличаться от значений этих характеристик в генеральной совокупности. Причем, чем меньше объем выборки, тем больше вероятность отклонения статистических характеристик от истин­ных, полученных по генеральной совокупности. Для устранения систематической ошибки при расчете дисперсии по выборочным данным необходимо использовать выражение:

Синтаксис:

ЭКСЦЕСС (число1; число2;...) См. также СКОС.

Результат:

Оценивает эксцесс по выборке. Аргументы:

число1, число2, ...: от 1 до 30 аргументов, для которых вычис­ляется эксцесс. Замечания:

• аргументы должны быть числами или именами, массивами или ссылками, содержащими числа;

• если аргумент, который является массивом или ссылкой, со­держит текстовые, логические значения или пустые ячейки, то такие значения игнорируются, однако ячейки с нулевыми значе­ниями учитываются;

• если задано менее четырех точек данных или если стандарт­ное отклонение выборки равняется нулю, то функция ЭКС­ЦЕСС помещает в ячейку значение ошибки #ДЕЛ/0!.

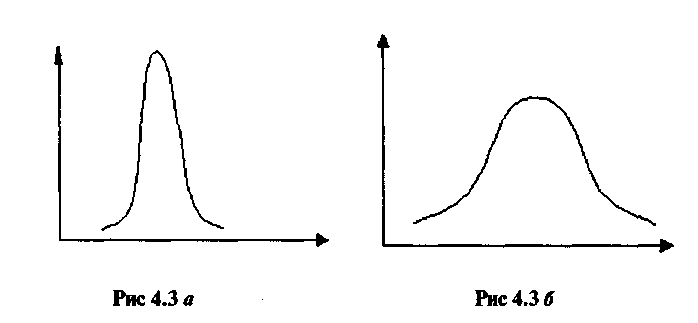
Математико-статистическая интерпретация: Эксцесс характеризует так называемую «крутость», т. е. остро­вершинность или плосковершинность распределения. Он может быть рассчитан для любых распределений, но в большинстве случаев вычисляется только для симметричных. Это объясняется тем, что за исходную принята кривая нормального распределения (Ek = 0), относительно вершины которой и определяется выпад вверх или вниз вершины эмпирического распределения. Функция ЭКСЦЕСС рассчитывает значение эксцесса как для симметрич­ных, так и для асимметричных распределений.

Наиболее точным и распространенным является определение эксцесса, основанное на расчете центрального момента 4-го по­рядка:

Применение данной формулы дает возможность вычислить значение эксцесса в генеральной совокупности. При этом если E_k > О, распределение островершинное, если E_k < 0 – плосковершинное.

Необходимо отметить, что функция ЭКСЦЕСС определяет значение эксцесса по выборочной совокупности, поэтому в ней ре­ализована формула расчета выборочного значения эксцесса.

Для приблизительного определения значения эксцесса по данным генеральной совокупности (или по данным выборочной совокупности, имеющей значительный объем) можно также пользоваться упрощенной формулой Линдберга

E_k=P- 38,29

где Р - доля (%) количества вариант, лежащих в интервале, рав­ном половине стандартного отклонения в ту и другую сто­рону от среднего значения;

38,29 - доля (%) количества вариант, лежащих в интервале, равном половине стандартного отклонения в ту и другую сторону от среднего значения ряда нормального распределения.

В примере 1 значение эксцесса расчитываеися по формуле ЭКСЦЕСС(B2:B10)