Применим синус к обеим частям данного нам неравенства

.

Упростим выражение . Пусть тогда , a .

Наше неравенство приняло вид .

Полученное иррациональное неравенство соответствует системе:

(см. рис. 35).

Р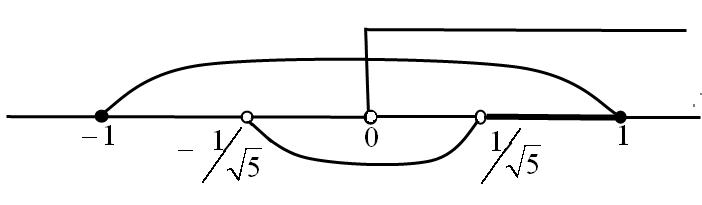 ешение системы .

С учетом условия имеем

Рис.35 .

Второй способ. .

Область определения неравенства

.

Строим графики функций и .

Следовательно, решением неравенства будет промежуток от точки, в которой до точки .

Равенство на ОДЗ равносильно . Упростим выражение .

Значит в качестве решения нашего неравенства получаем двойное неравенство:

Третий способ.

О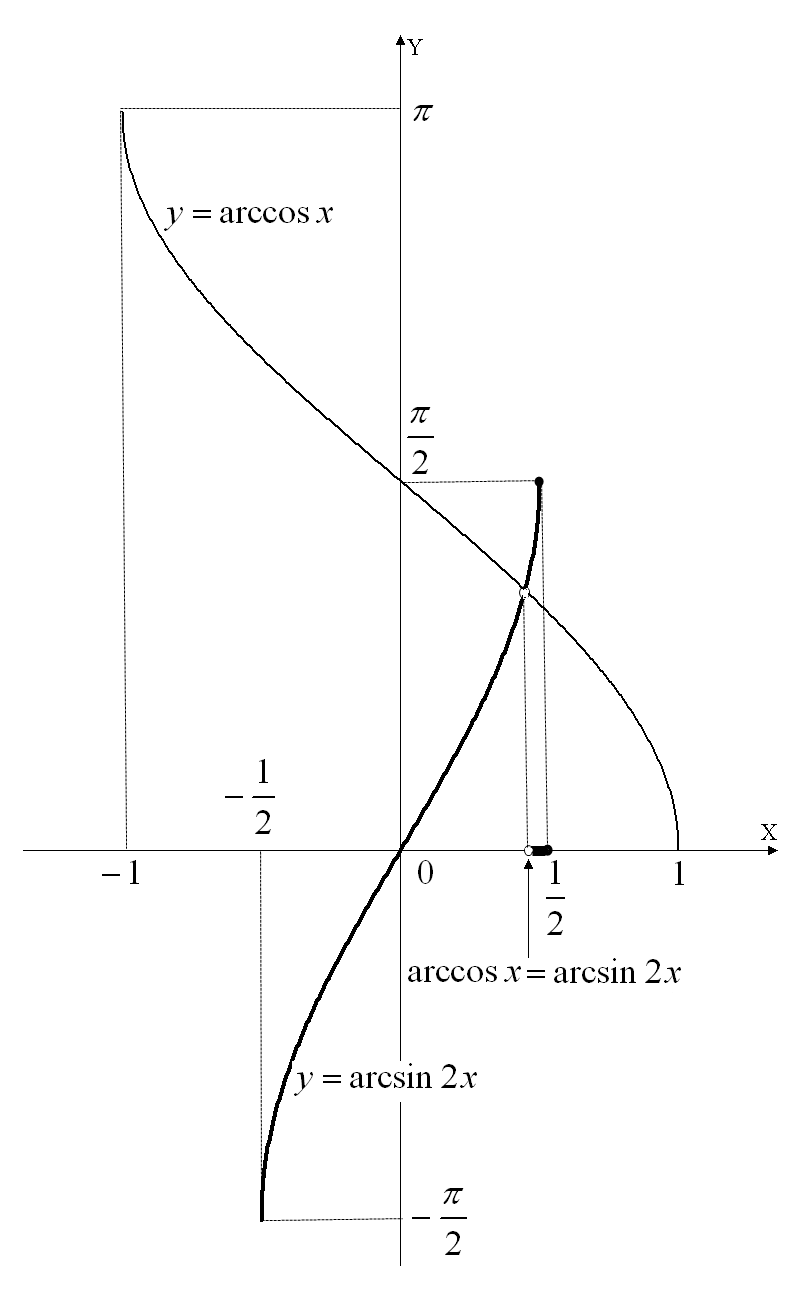 бласть определения неравенства – отрезок . Воспользуемся свойством монотонности. Слева функция убывает, а справа функция возрастает. Равенство

справедливо не более чем в одной точке , где , а правее этой точки возрастающая функция больше убывающей. Следовательно, неравенство справедливо на промежутке (см. рис. 36). Найдем , решив уравнение . Применим функцию , получим

Рис. 36

;

. Имеем .

Ответ. .

Задание 22. .

Решение.

Поскольку расположение графиков функций и все же не столь очевидно, то графический способ не будем использовать.

Обе части неравенства принимают значения из промежутка , на котором функция монотонно убывает, тогда ; .

Упростим выражение . Пусть , тогда , . Получим

Следовательно, ; ; ;

Имеем совокупность двух систем:

Итак решение неравенства .

Найдем ОДЗ данного нам по условию неравенства:

С учетом области допустимых значений .

Ответ. .

Задание 23. .

Решение.

Область определения неравенства .

Так как , то на области определения получим неравенство

. Корни квадратного трехчлена

.

Корень разбивает промежуток на два: и . Возьмем по одной точке из каждого промежутка и подставим в начальное неравенство.

Пусть имеем ; . Неравенство неверное.

Таким образом, неравенство на этом промежутке не выполняется.

Пусть , имеем ; . Неравенство верное.

Второй промежуток является решением.

Ответ. .

Задание 24. .

Решение.

Область определения неравенства , так как в точках функция принимает значения , в которых тангенс не определен; а функция принимает значения и , в которых, в свою очередь, котангенс не определен.

Воспользовавшись тождеством , имеем ; ; .

Упростим и решим неравенство

.

Неравенство выполнено при .

Отметим, что неравенство можно было решить иначе. Применим к обеим частям неравенства функцию , монотонно возрастающую на всей числовой оси

.

Так как область значений функции ‑ отрезок , а , то есть , можем применить к обеим частям неравенства функцию , монотонно возрастающую на отрезке

,

а с учетом ОДЗ .

Ответ. .