1. Простейшие неравенства с аркфункциями
Решим
простейшие неравенства с обратными
тригонометрическими функциями
;
;
;
.
Задание
1.
.
Решение.
Такие
неравенства очень удобно решать
графически, что доступно и наглядно
для учащихся (см. рис. 1). Строим графики
функций
и
.
Е
сли
,
то
ни при каких
.
Значит, в этом случае неравенство
решений не имеет.
Если
-
то в качестве решения получим промежуток
.
Если
,
то
для любых значений
из области определения функции
,
то есть
Рис.1. 
.
Ответ.
Если
,
то
;
если
,
то
;
если , то нет решений.
Следующие три неравенства решаются аналогично.
З
адание
2.
.
Решение.
График полностью иллюстрирует решение (см. рис. 2).
Ответ.
Если
то
;
если
,
то
;
если
,
то нет решений.
Рис.2
Задание
3.
.
Р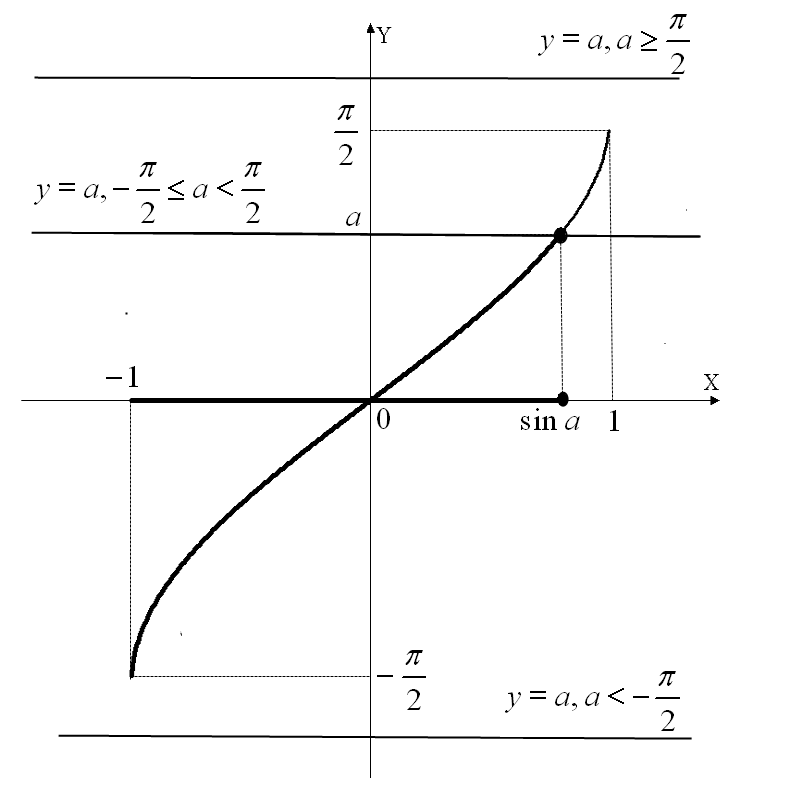
ешение.
Решение изображено на графике (см. рис. 3).
Ответ. Если , то нет решений неравенства;
если
,
то
;
если
a>
,
то
.
Рис.3
З
адание
4.
.
Решение.
Аналогично решается и это неравенство (см. рис. 4).
Ответ.
Если
,
то нет решений;
если
,
то
;
если , то .
Рис.4
Простейшие
неравенства вида
можно решать аналогично, а можно свести
к рассмотренным, если учесть известное
нам тождество
.
Для закрепления материала полезно
прорешать все простейшие неравенства
с аркфункциями.
2. Неравенства, сводящиеся к простейшим неравенствам с аркфункциями
Рассмотрим примеры усложненных, но относящихся к простейшим, неравенств с аркфункциями.
Задание
5.
.
Решение.
В
ведем
обозначение
.
Найдем область допустимых значений
неравенства. Из определения арксинуса
следует ограничение
,
,
;
.
Известно,
что областью значений функции
будет отрезок
,
то есть
на всей области определения
(см.
рис. 5).
Значит, решением данного неравенства является множество .
Рис.5
Ответ.
.
Задание
6.
.
Решение.
Первый
способ. Решение
аналитическое, без применения графика
функции
.
Областью определения неравенства
является отрезок
.
Пусть
.
Решим неравенство
:
,
тогда
.
Возвращаемся к переменной
:
.
Применяя
функцию
ко всем частям неравенства, имеем
так как
возрастает при
.
Получили неравенство
(см. рис. 6).
С
учетом ОДЗ:
, имеем систему
Рис.6 Сравним
и 1. Так как
,
то
так как
возрастает на промежутке
,
а значит
и, аналогично,
.
Следовательно,
.
Второй способ. .
Обе
части данного неравенства положительны,
значит можно извлечь квадратный корень
из обеих частей неравенства:
,
тогда имеем
Решим данное двойное неравенство графически (см. рис. 7).
Получим .
Ответ.
.
З
адание
7.
.
Решение.
Первый
способ: Так
как обе части данного неравенства
принимают значения из отрезка
,
а на нем функция
возрастает, имеем
.
Решим это неравенство
Рис.7 методом интервалов
(
см. рис. 8).
.
Рис.8 
и
.
С учетом области допустимых значений данного нам неравенства , имеем систему неравенств
(см.
рис. 9)
Рис.9
и
.
Второй способ. .
Пусть
тогда
.
Решим графически последнее неравенство (см. рис. 10).
,
то есть
.
Т
ак
как все части неравенства положительны,
значит
.
Следовательно, имеем совокупность неравенств
Решением будет
и .
Рис.10 Ответ.
.
Задание
8.
.
Решение.
Первый способ. Обе части данного нам неравенства принимают значения из области , на которой функция возрастает, значит по монотонности
;
Решая,
имеем
,
так как функция
возрастающая.
Найдем ОДЗ данного нам неравенства.
;
;
.
То есть
.
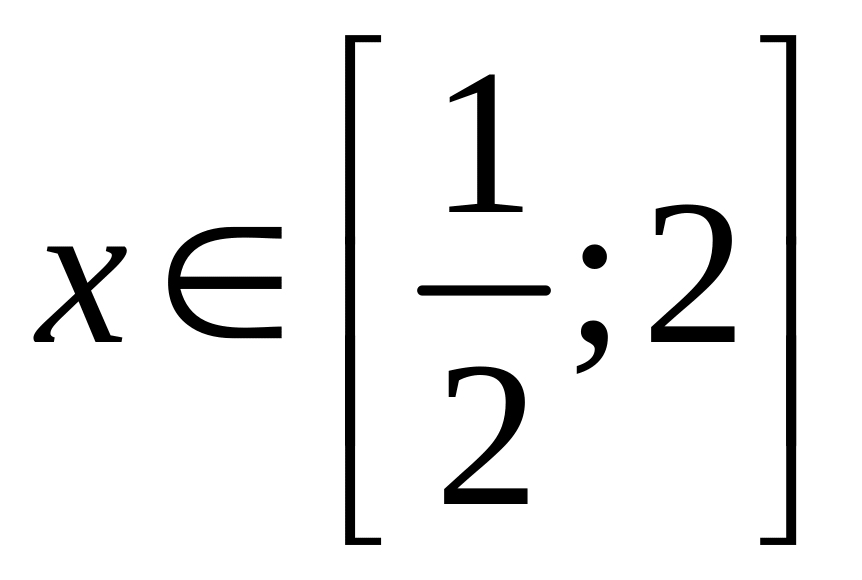Итак, имеем систему неравенств
Откуда
следует, что
.
Ответ. .
Второй
способ.
.
Пусть
,
тогда
.
Проиллюстрируем решение последнего
неравенства графически (см. рис 11).
;
;
;
Ответ. .
Задание
9.
.
Решение.
Первый способ.
П
рименим
синус к обеим частям неравенства, так
как
возрастает на области
,
то имеем
;
;
.
Так
как
возрастает на интервале
,
то
,
.
Найдем область допустимых значений данного нам неравенства. Из определения арксинуса, следует
;
Рис.11
и используя монотонность на интервале получим
Итак, имеем систему неравенств
Следовательно,
.
Второй способ.
Пусть
,
тогда
.
Мы получили такое же неравенство, как
и в задании
8 при
решении вторым способом, а это значит,
что (см. рис. 11)
Решим графически последнее неравенство (см. рис. 12).
Имеем,
что
Третий способ. .
Воспользуемся монотонностью функции :
и
областью определения
.
Получим
,
,
.
Рис.12
Ответ. .
Задание
10.
.
Решение.
Первый способ. Обе части данного нам неравенства принимают значения из области а на этом отрезке функция синус возрастает, тогда применив синус
.
С учетом ОДЗ имеем систему неравенств:
тогда
получаем систему
Р
ешим
неравенство (1) (см. рис 13).
;
;
.
Рис.13
Решим неравенство (2) (см. рис 14).
;
.
. Рис.14
И
так,
решая систему неравенств (1) и (2), имеем
(см. рис 15).
.
Рис.15
Ответ. .
Второй
способ.
.
Решим
неравенство графически. Строим графики
,
где
и
(см. рис. 16).
Получаем
двойное неравенство:
,
то есть
,
,
ч
то
сводится к решенной выше системе
неравенств
Ответ. .
Третий способ. .
Рис.16
С учетом области значений функции имеем неравенство
.
Используя
монотонность функции
на отрезке
,
имеем
.
И вновь получаем систему
Ответ. .
Задание
11.
.
Решение.
Первый
способ. Обе
части неравенства принимают значения
из области
,
на которой функция
убывает, значит
;
.
Найдем ОДЗ данного нам неравенства:
,
то есть, получаем систему неравенств
С учетом полученного выше неравенства, имеем систему неравенств:
Решим неравенство (1) из последней системы:
;
Р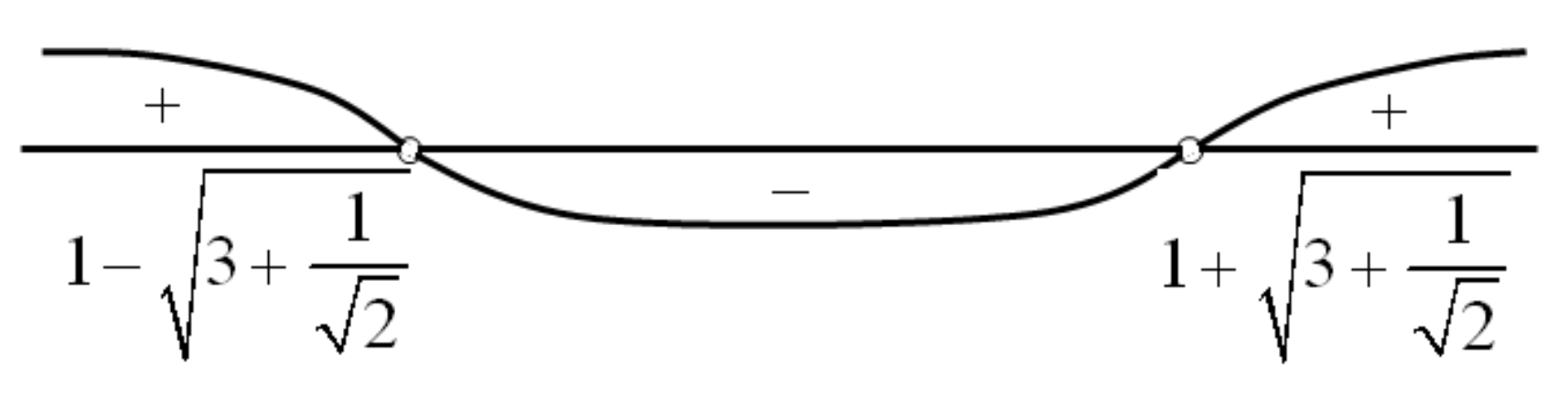
ешим
это неравенство методом интервалов
(см. рис 17).
Рис.17
Имеем
(см. рис.17):
.
Решим
неравенство (2)
.
;
Решим систему неравенств (1) и (2) (см. рис 18).
Рис.
18
и
.
Ответ.
.
Второй
способ.
Р
ешаем
графически данное неравенство. Строим
графики
и
,
где
(см. рис. 19).
то
есть
.
,
откуда следует система неравенств (1)
и (2) рассмотренная выше.
Рис. 19
Ответ. .
Задание
12.
.
Решение.
Пусть
,
то
.
Решим неравенство
;
.
Следовательно,
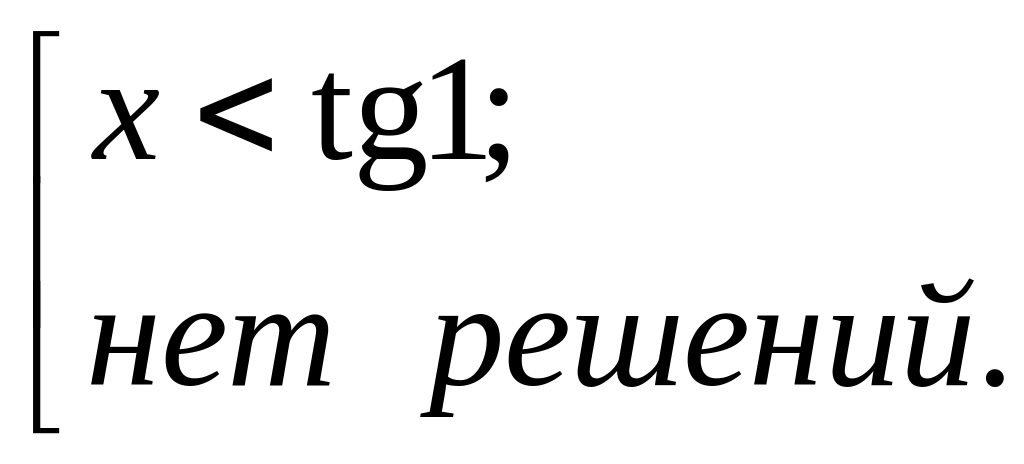
(см.
рис 20).
Рис.20
Ответ. .