3. Неравенства с аркфункциями повышенной сложности

Рассмотрим более сложные неравенства с обратными тригонометрическими функциями. Здесь часто придется применять к обеим частям неравенства синус или косинус, тангенс или котангенс. Чтобы при этом множество решений исходного неравенства не менялось, необходимо, чтобы обе части неравенства лежали внутри или совпадали с промежутком монотонности функций соответственно. Если множество значений обеих частей неравенства не укладывается в один и тот же промежуток монотонности основной тригонометрической функции, то неравенство следует тождественно преобразовать или выделить промежутки монотонности и решать неравенство отдельно на каждом таком промежутке.

Рассмотрим примеры.

Задание 13. .

Решение.

Найдем ОДЗ неравенства: .

Область значений функции ‑ интервал 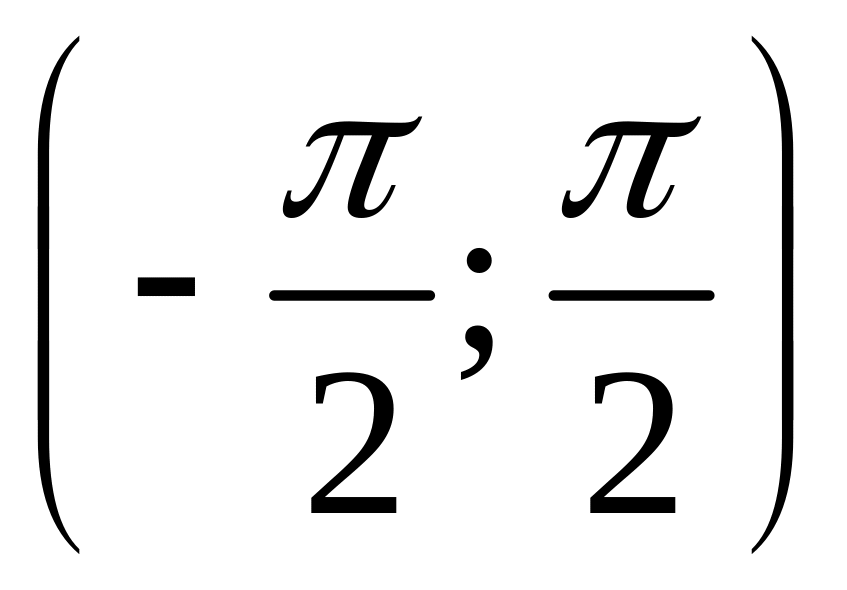, поэтому левая часть неравенства принимает значения из интервала , на котором ни одна из основных тригонометрических функций не является монотонной. Преобразуем данное нам неравенство

.

Прежде, чем решать преобразованное неравенство, попробуем получить ограничения на переменную . Для этого оценим сначала функцию

Функция ограничена. Значит, неравенство необходимо рассматривать при

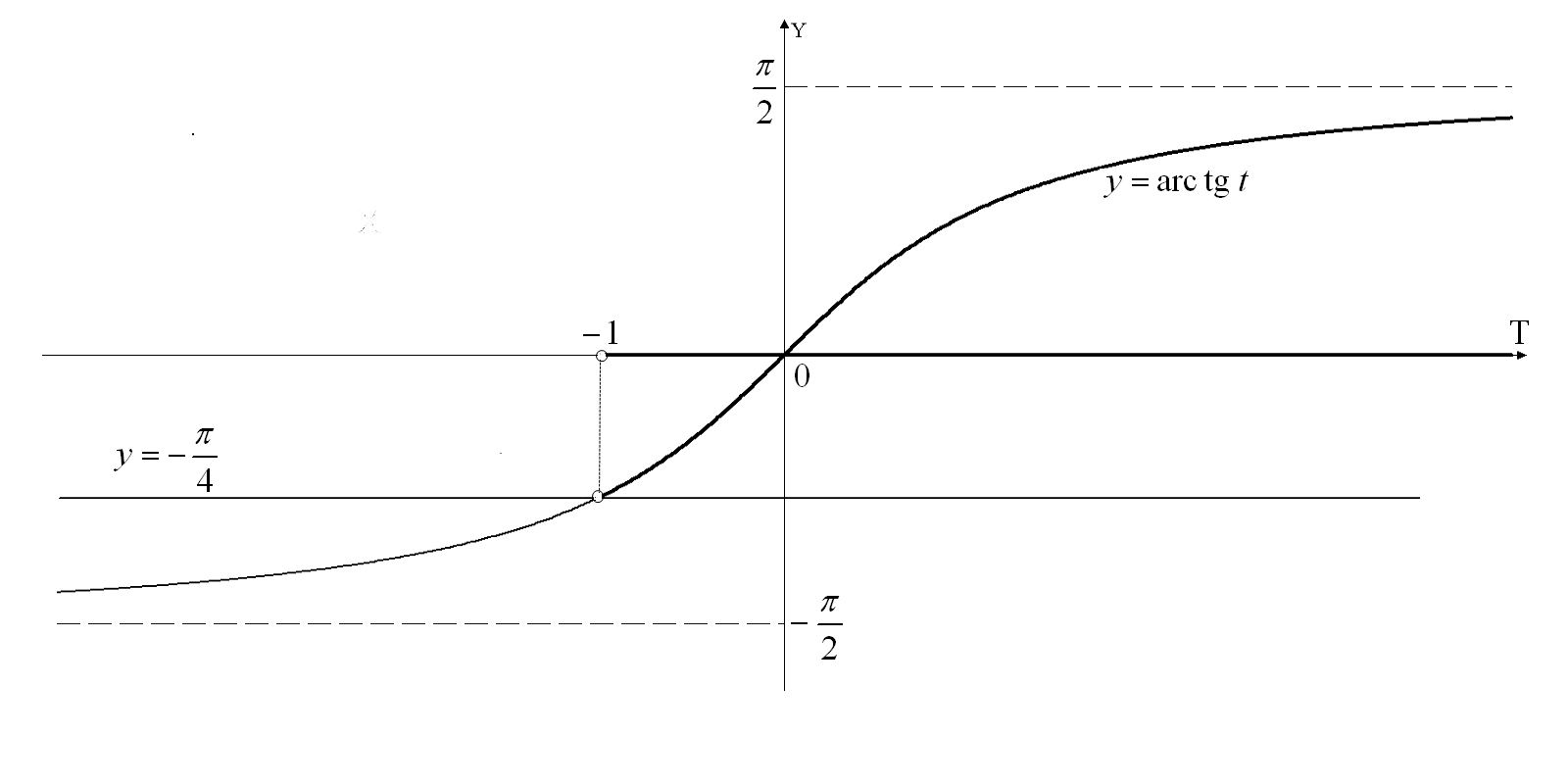
; (см. рис.21).

Рис.21

Теперь можем получить ограничения на переменную :

.

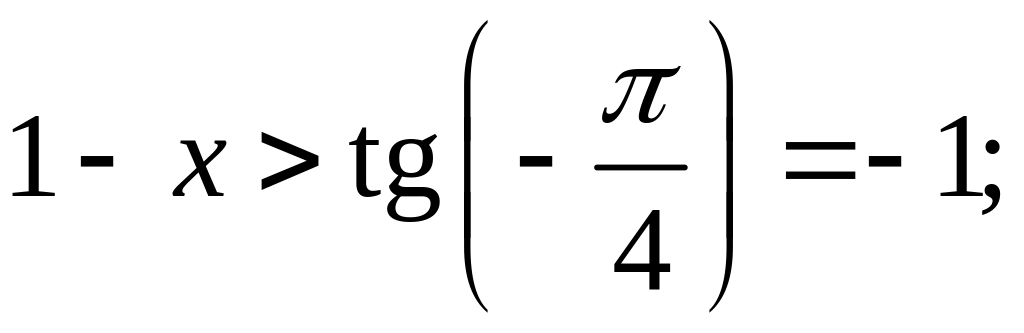
Возвращаемся к решению неравенства . При условии , обе части неравенства принимают значения из отрезка и от обеих частей можно взять тангенс, так как он монотонно возрастает на указанном интервале.

.

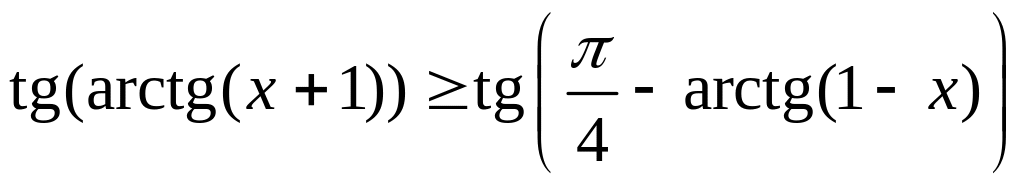
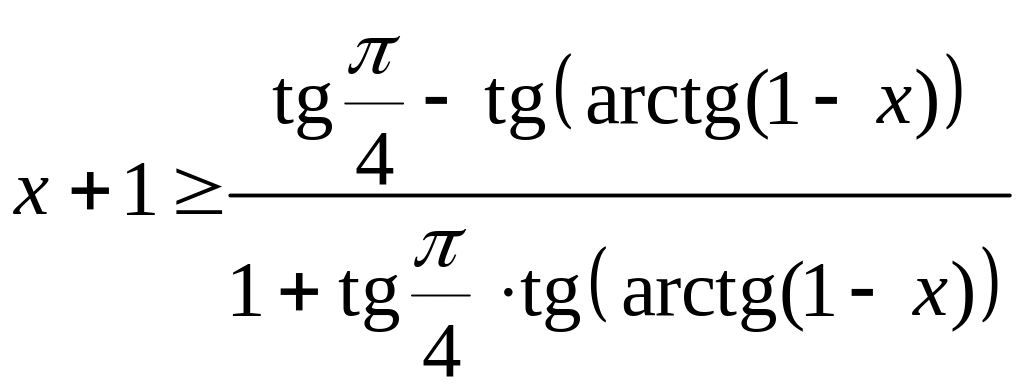
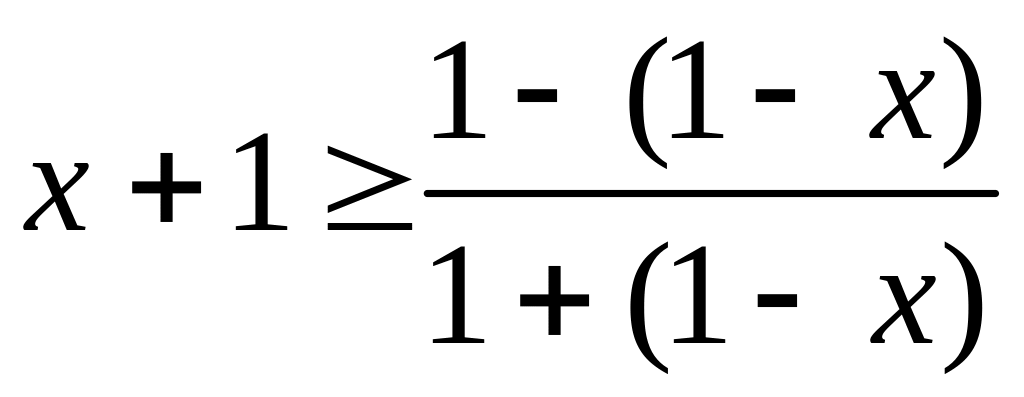
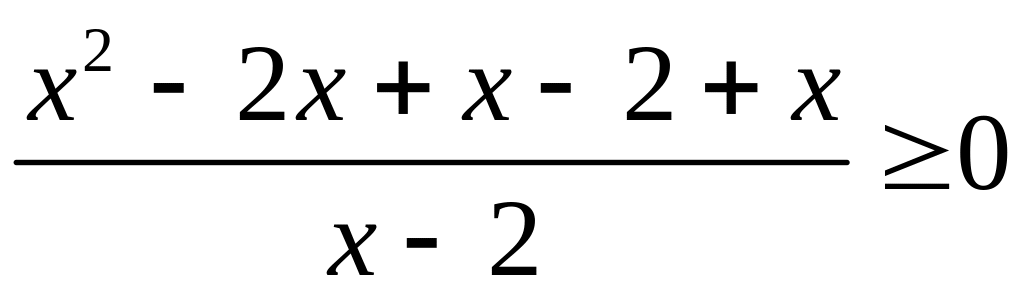
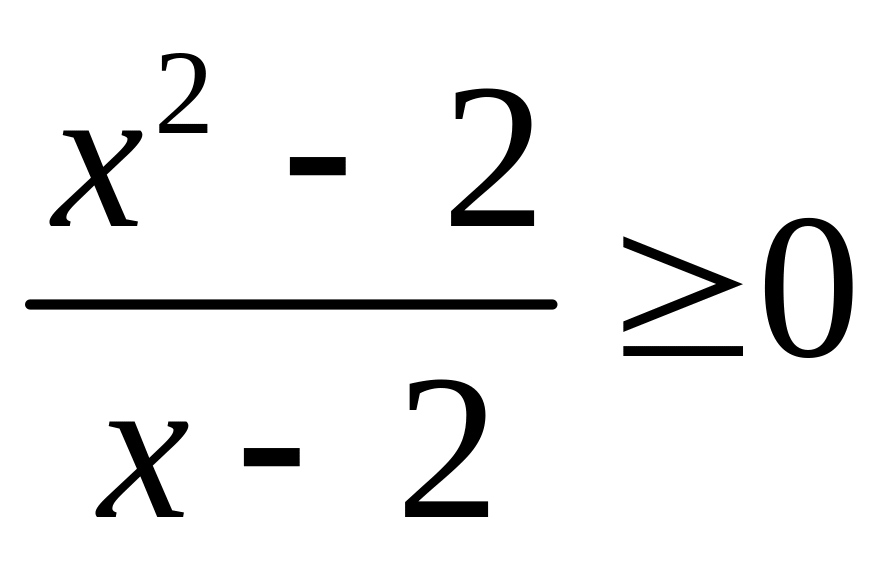
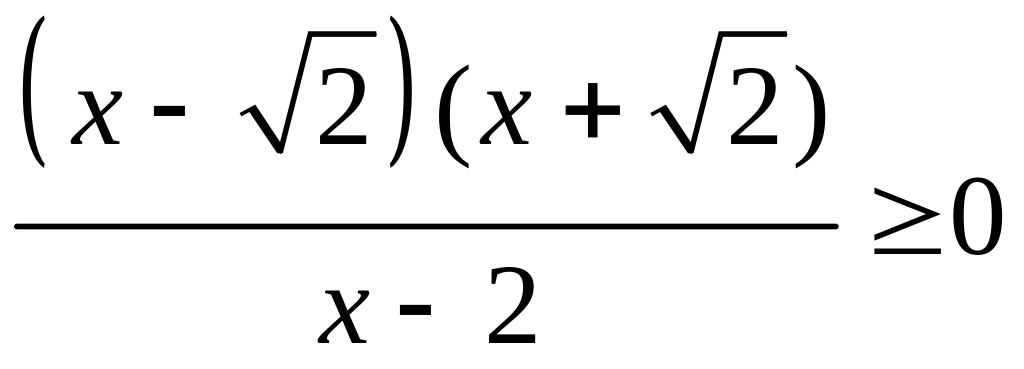Р ешение неравенства имеет вид (см. рис. 22). С учетом того, что , то .

Рис 22

Ответ. .

Задание 14. .

Решение.

Найдем область допустимых значений неравенства из решения системы

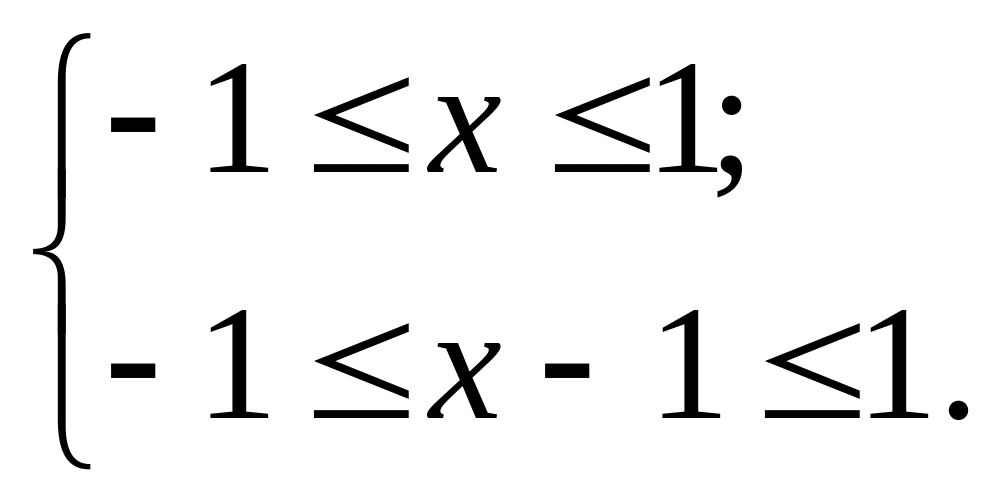
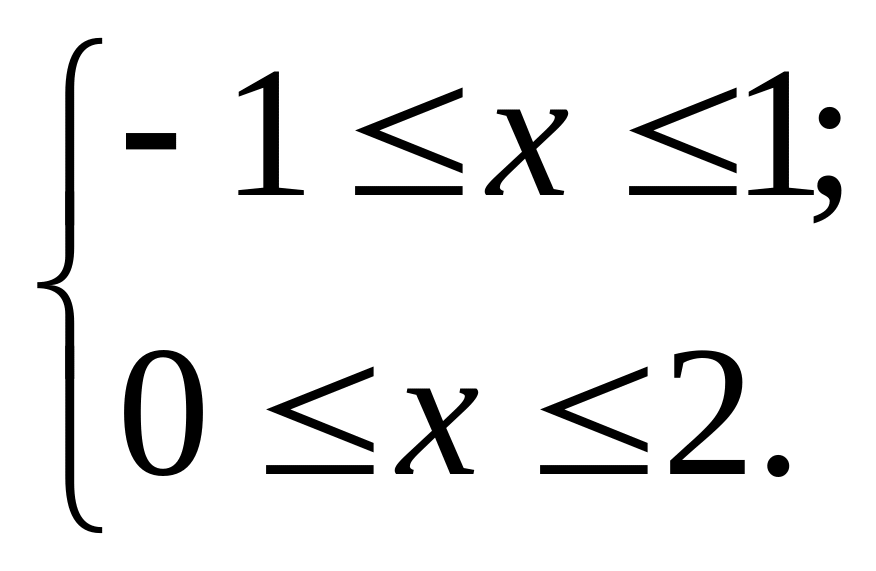
Откуда следует, что .

На этой области определения обе части неравенства принимают значения на отрезке . Покажем это, применив функцию ‑ убывающую:

Справа имеем ;

;

;

Аналогично слева: то ;

Значит ;

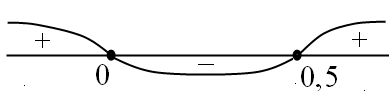
Значит можно взять косинус от обеих частей данного нам по условию неравенства, учитывая, что косинус на промежутке убывает.

;

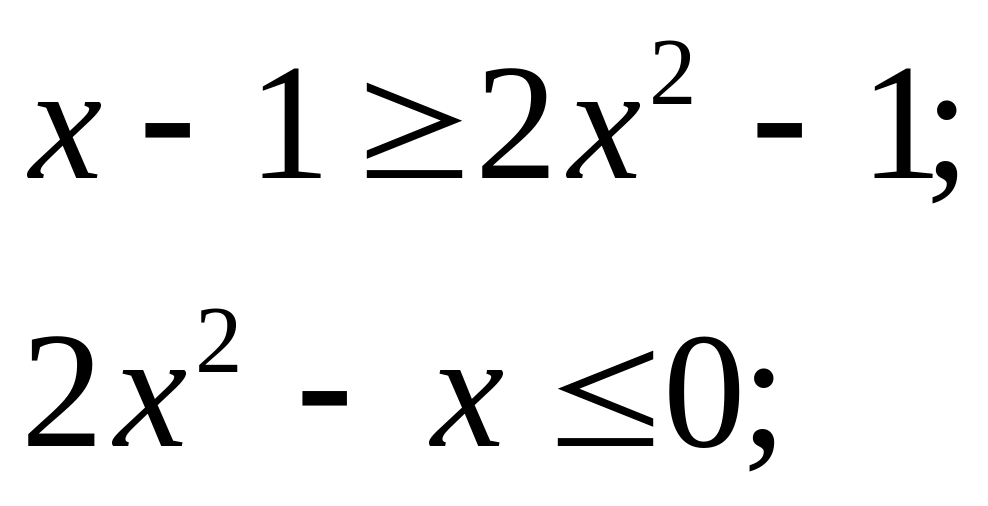
(см. рис. 23) Рис.23

Так как ОДЗ: то окончательно имеем .

Ответ. .

Задание 15. .

Решение.

Первый способ. Найдем область определения неравенства из решения системы:

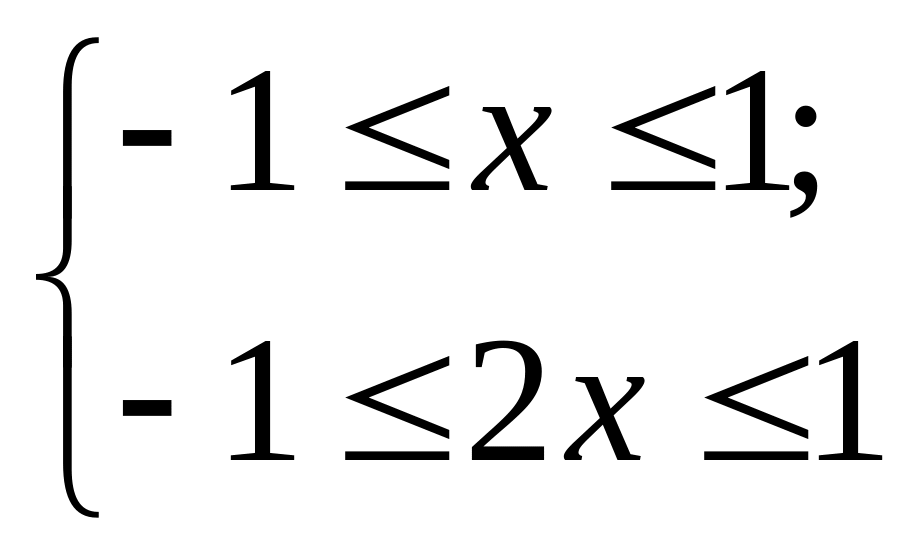
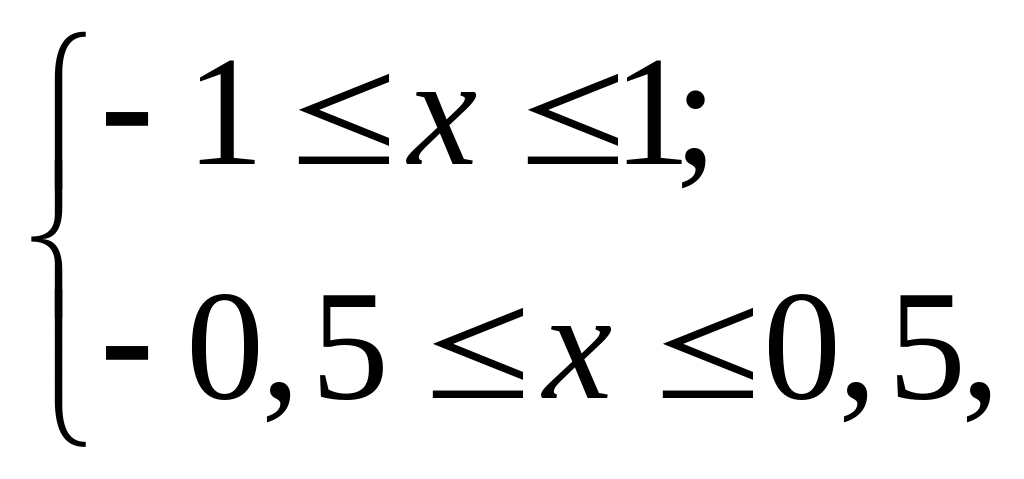то .

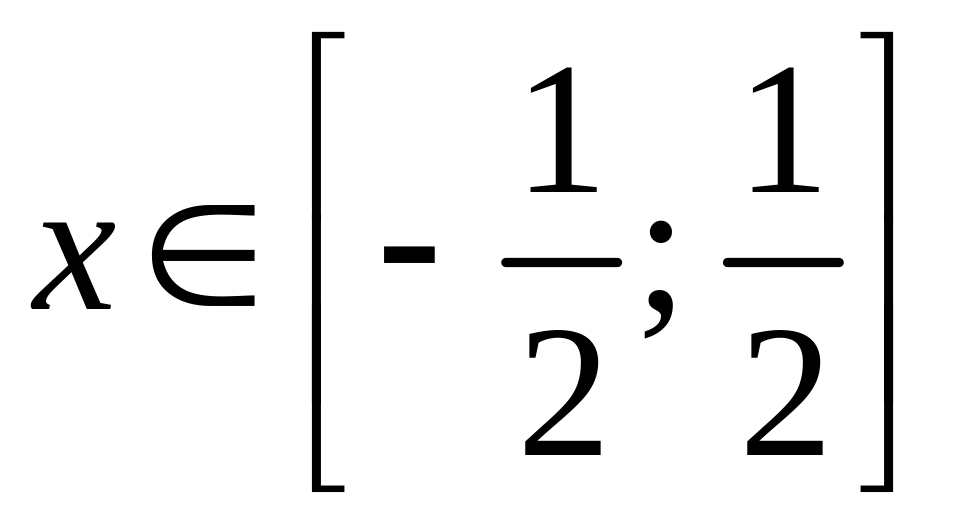Так как обе части нашего неравенства принимают значения из области , то применим синусы к обеим частям неравенства, учтем при этом, что функция на этом отрезке возрастает

;

;

С учетом ОДЗ имеем .

Второй способ. Воспользуемся свойством монотонности функции . Заметим, что при , следовательно, при . Область определения неравенства: . На этом отрезке функция возрастает. Поэтому при ( ) имеем , а при ( ) имеем

.

В нашем неравенстве должно быть , а с учетом ОДЗ, имеем .

О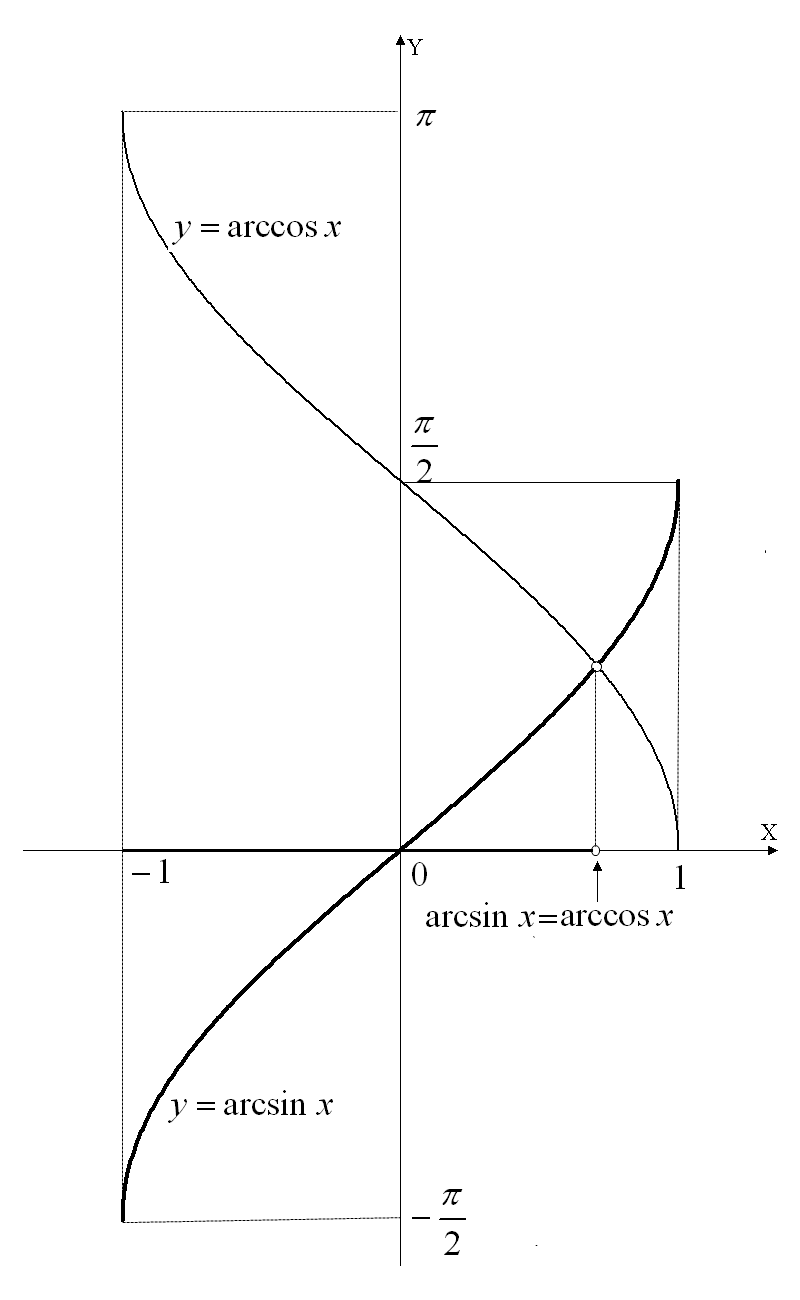 твет. .

Задание 16. .

Решение.

Первый способ. Решим неравенство графически. Для этого строим графики функций и (см. рис.24).

Очевидно, что с учетом монотонности функций (возрастает) и (убывает) решением неравенства будет промежуток от до точки, в которой , или,

Рис.24

применив к обеим частям равенства , до точки, в которой . Промежуток принял вид

Упростим выражение , входящее в двойное неравенство.

Пусть , тогда где .

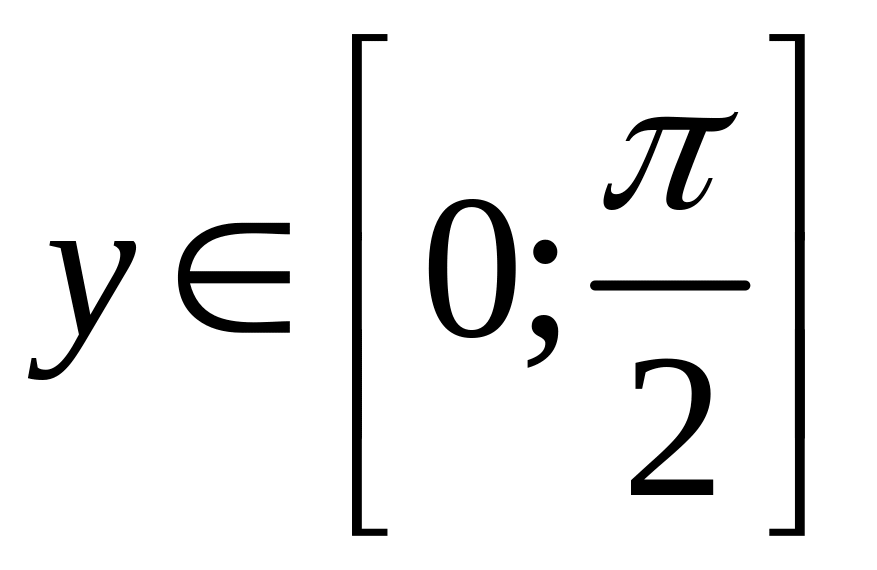Значит наше неравенство запишется в виде Имеем систему

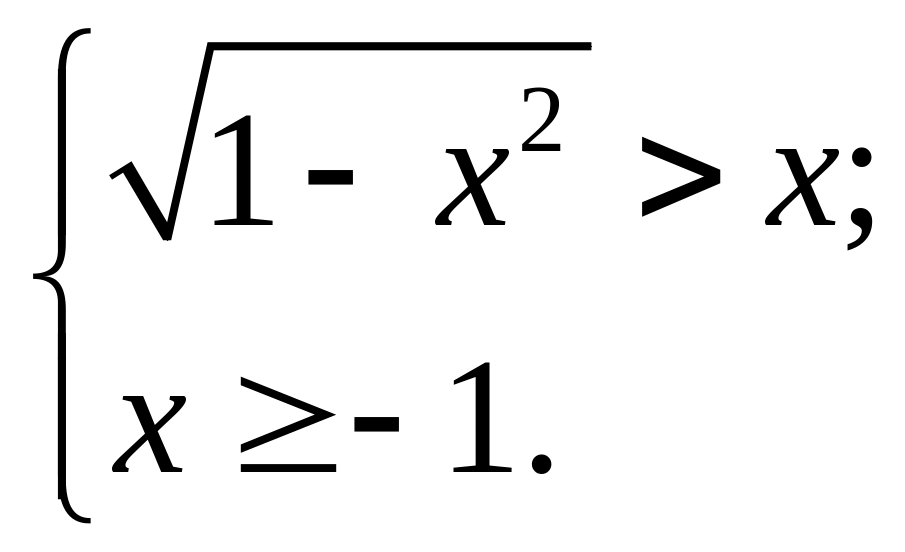
Её решением будет совокупность двух систем неравенств:

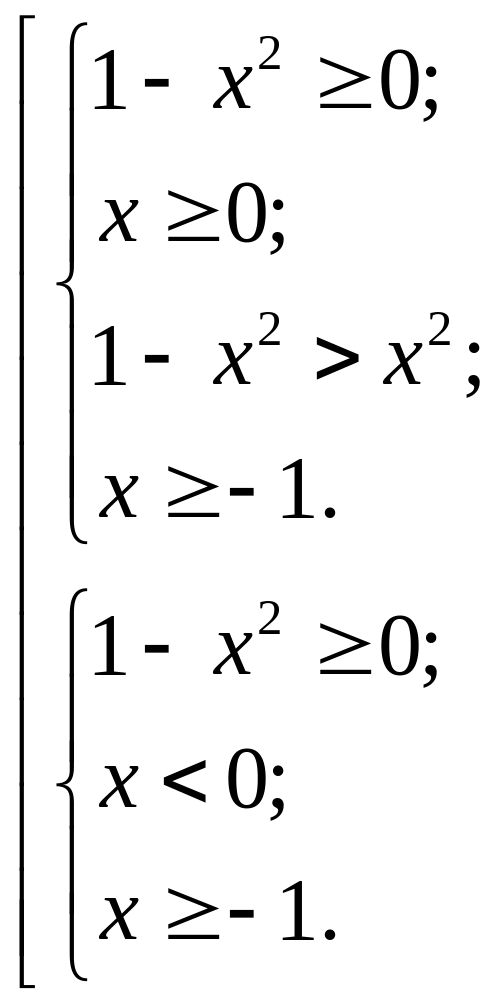
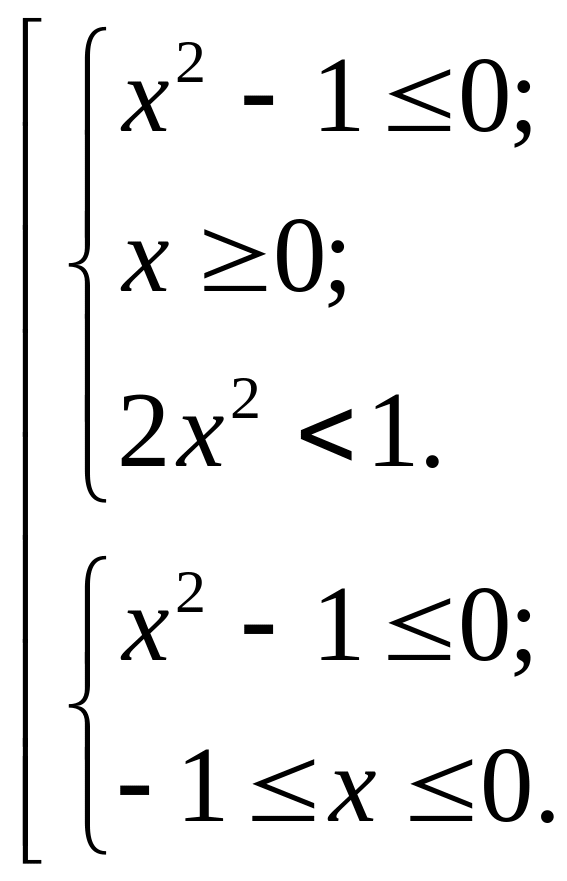
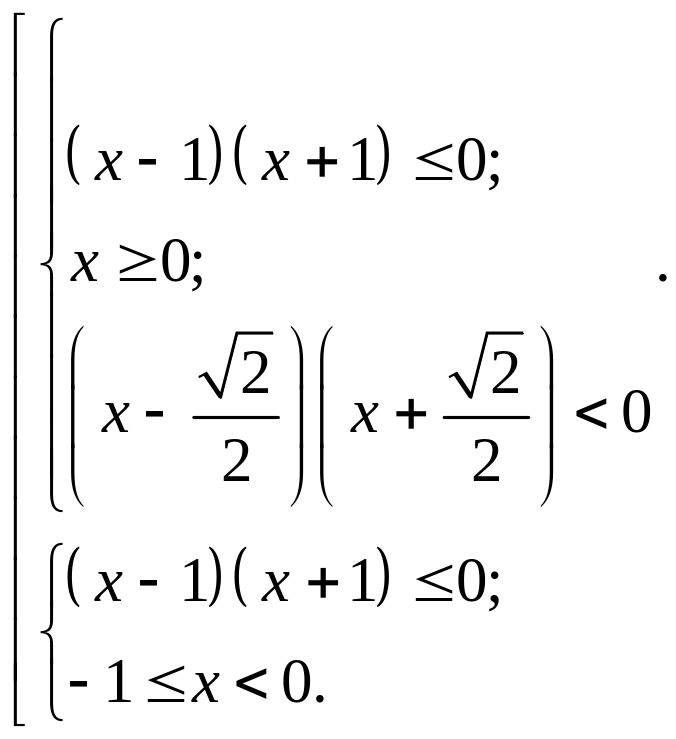
Р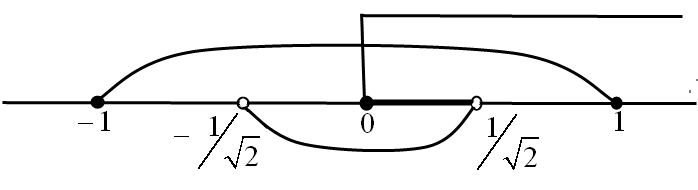 ешим каждую из полученных систем (см. рис. 25 и рис. 26).

Решение первой системы: имеем

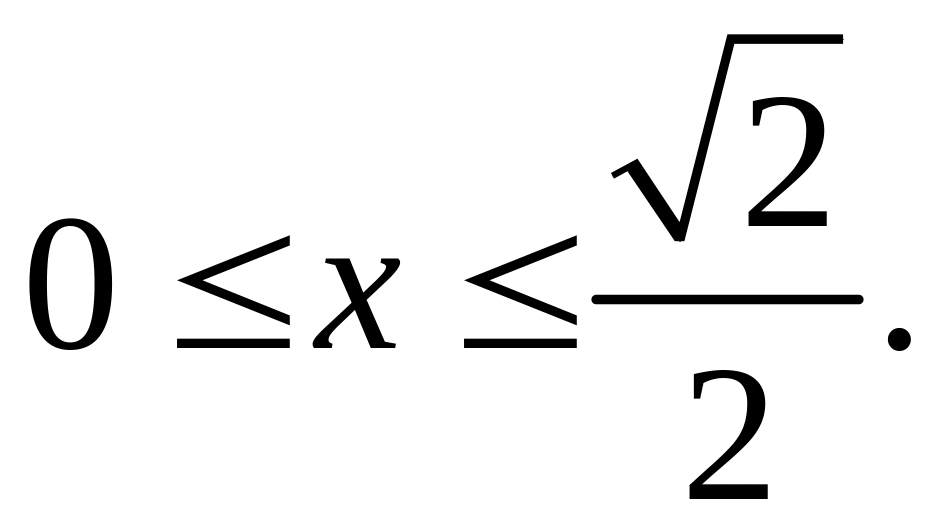
Рис.25

Р ешение второй системы: имеем .

Рис 26

Объединив, получим окончательно .

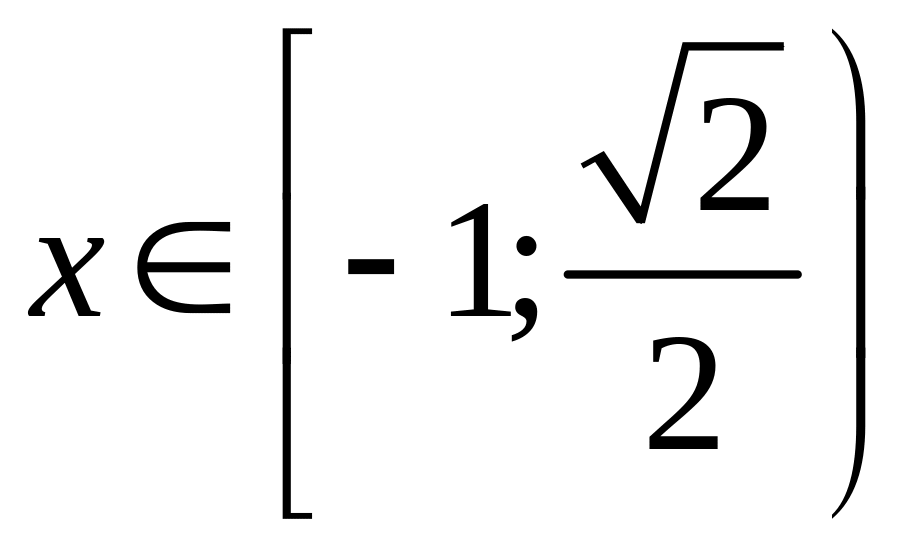Второй способ. .

Так как на общей области определения функция возрастает, а функция убывает, то если они и могут принять одинаковое значение, то только одно. При этом синус должен быть равен косинусу. Это известное значение 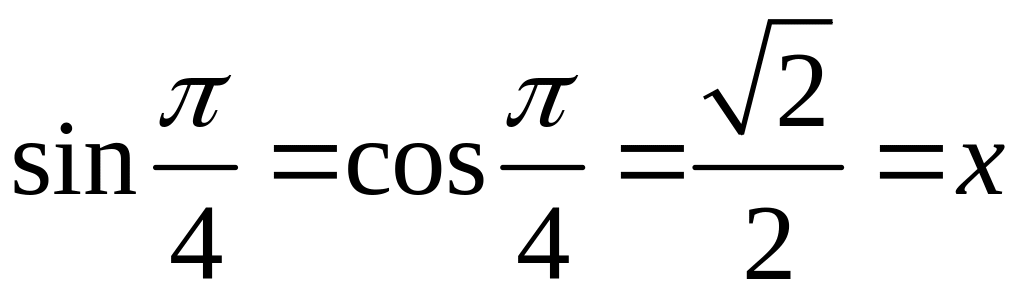. Следовательно, неравенство справедливо только до этого значения. С учетом области определения . (заметим, что 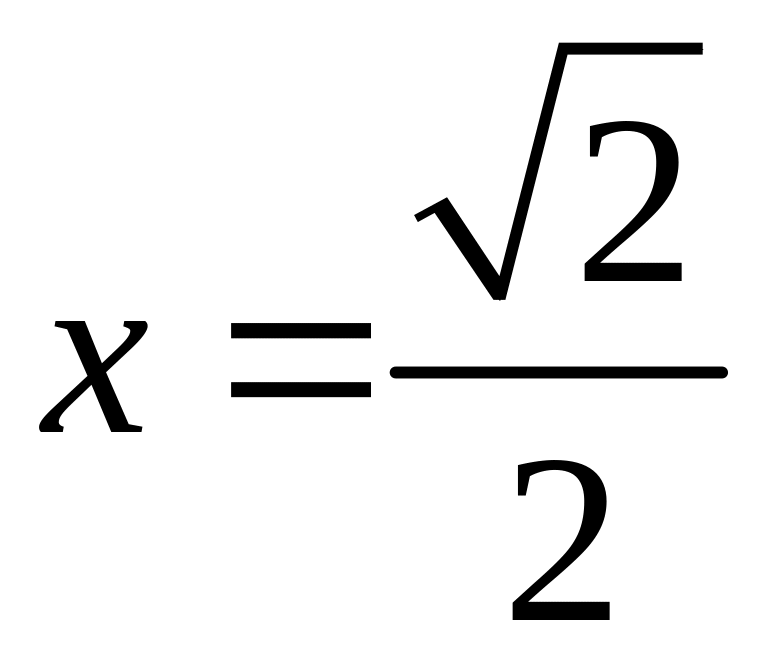, решение уравнения из первого способа).

Третий способ. .

М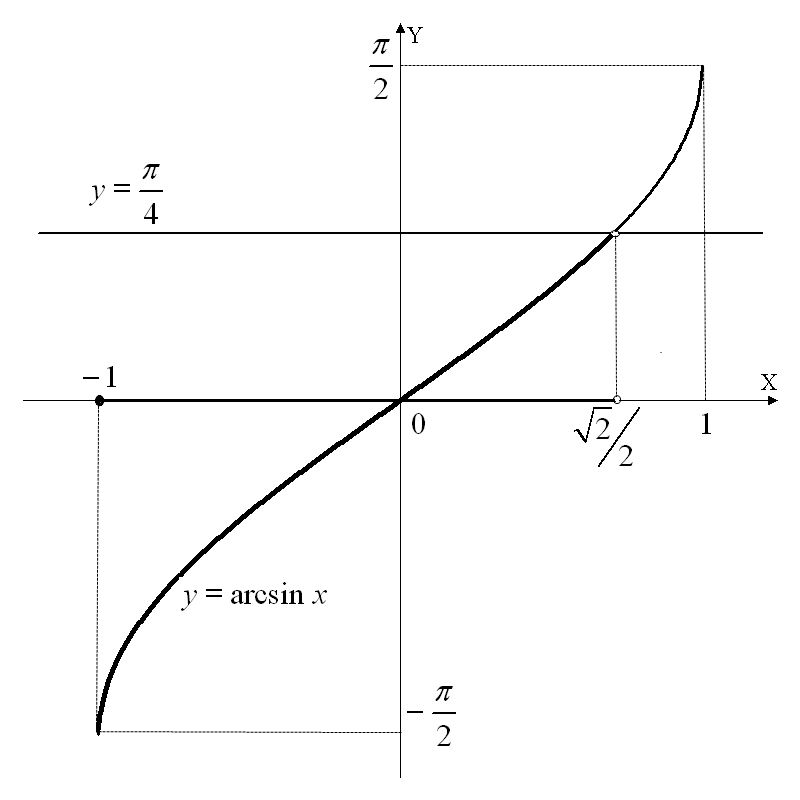 ожно решить это неравенство, используя известное равенство

.

Решение становится намного проще и красивее:

;

(см. рис. 27).

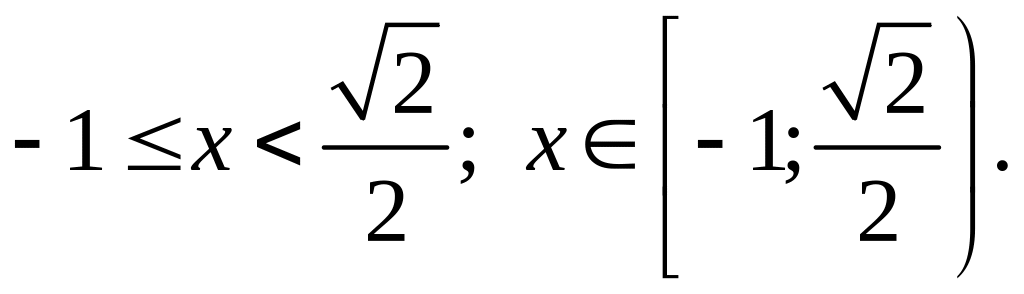Рис.27 Ответ. .

Задание 17.

Решение.

;

;

;

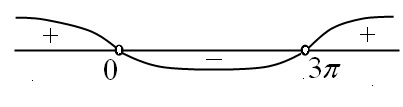
Пусть , где Тогда (см. рис. 28). Значит,

Рис. 28

С учетом области определения для , имеем .

С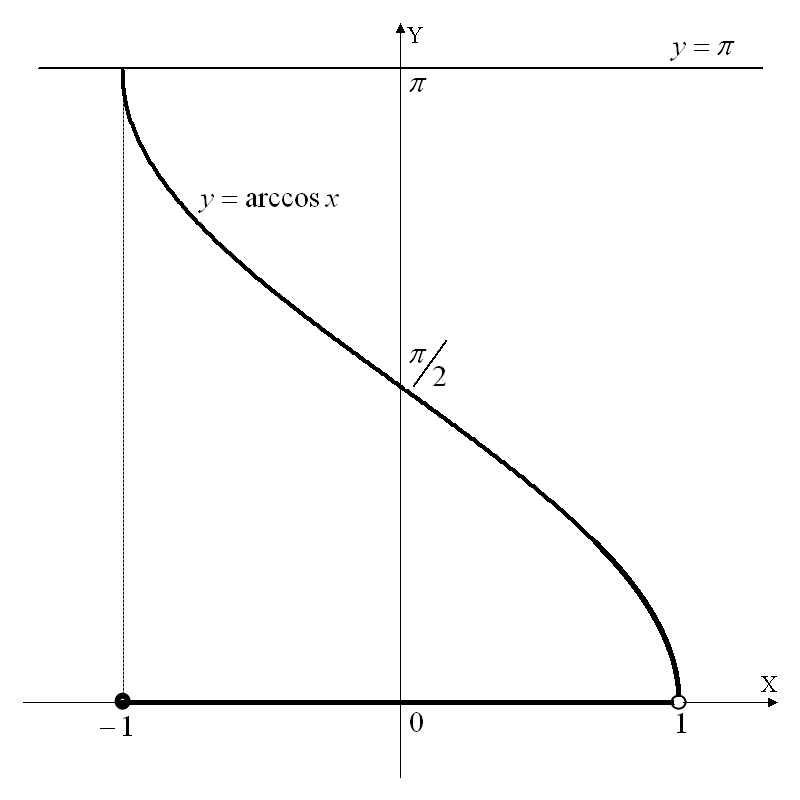 ледовательно, (см. рис. 29). Применяя косинус ко всем частям неравенства, и учитывая его монотонное убывание на отрезке , имеем , то есть

Ответ.

Задание 18.

.

Решение.

Первый способ. Найдем область допустимых значений переменной из решения системы неравенств

Рис.29

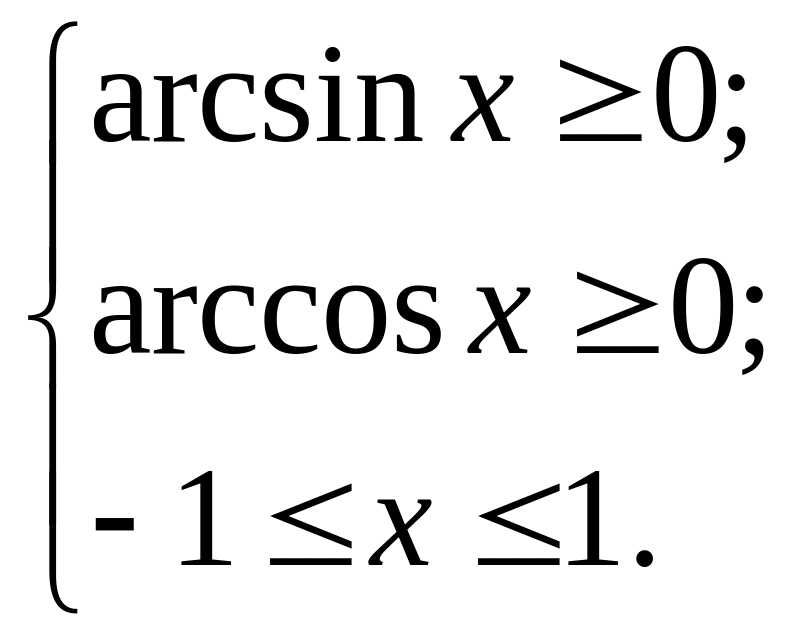
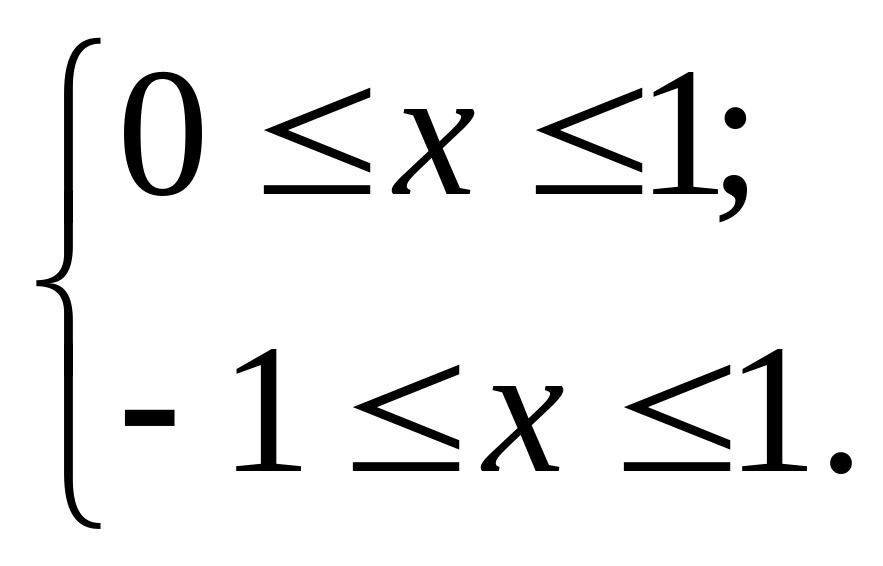. Откуда ОДЗ:

Обе части неравенства положительны, поэтому при возведении в квадрат сохраняется равносильность выражений.

; воспользуемся формулой

.

;

;

; вновь обе части неравенства положительны,

; перейдем к одной функции арксинус:

Пусть , тогда

; ;

;

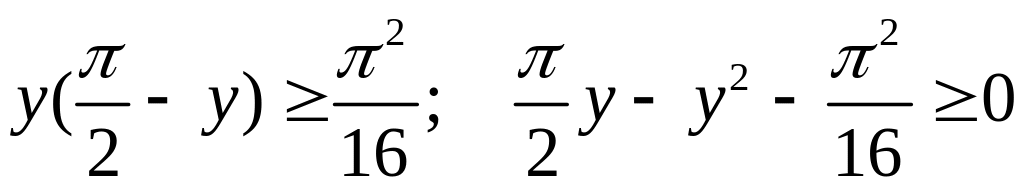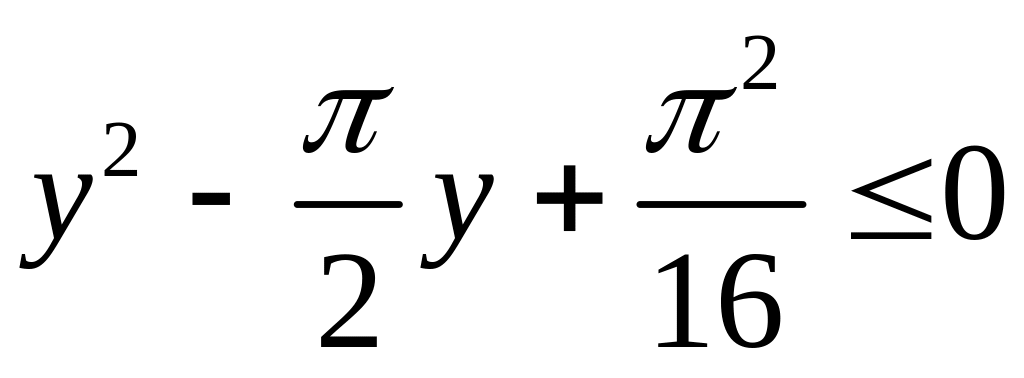Значит

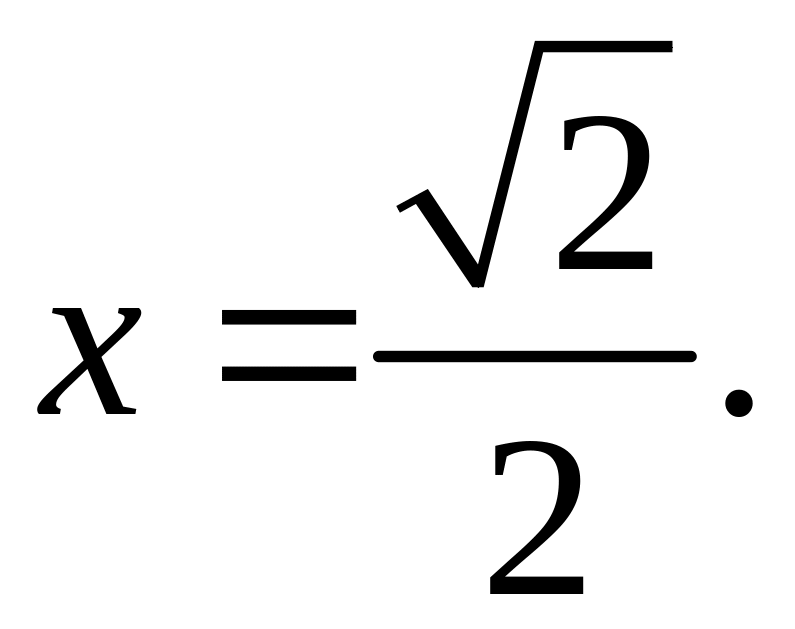
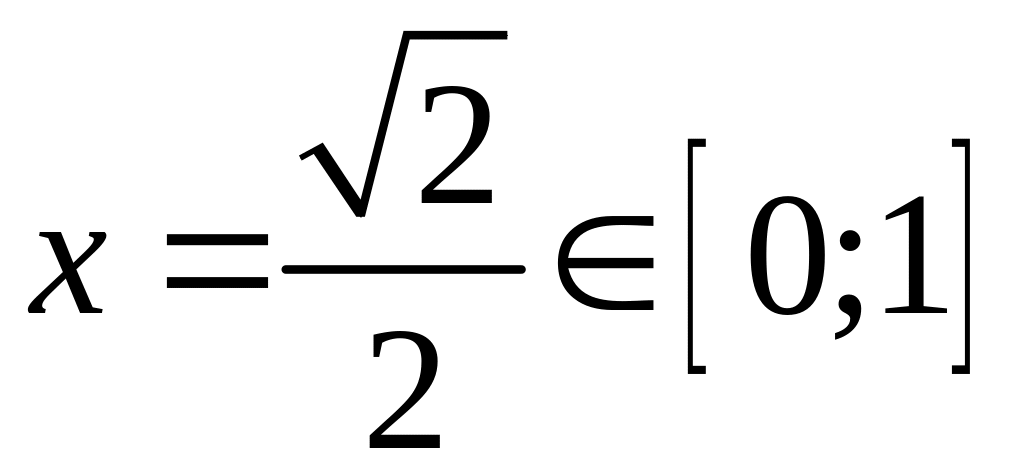Проверим на принадлежность области допустимых значений неравенства . Найденное значение . Следовательно

Второй способ. .

Так как функции и связаны уравнением

,

то заменив

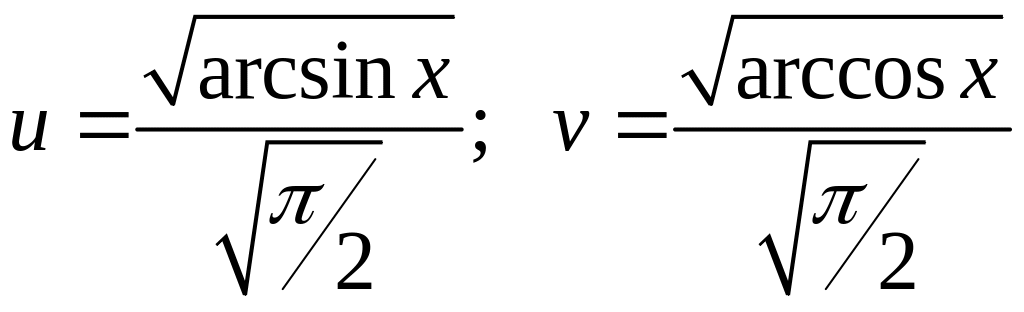
п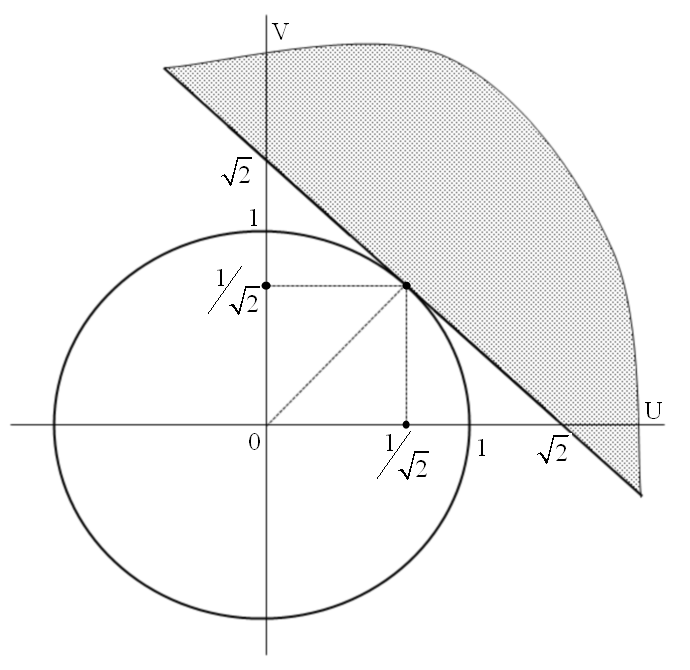 олучим смешанную систему 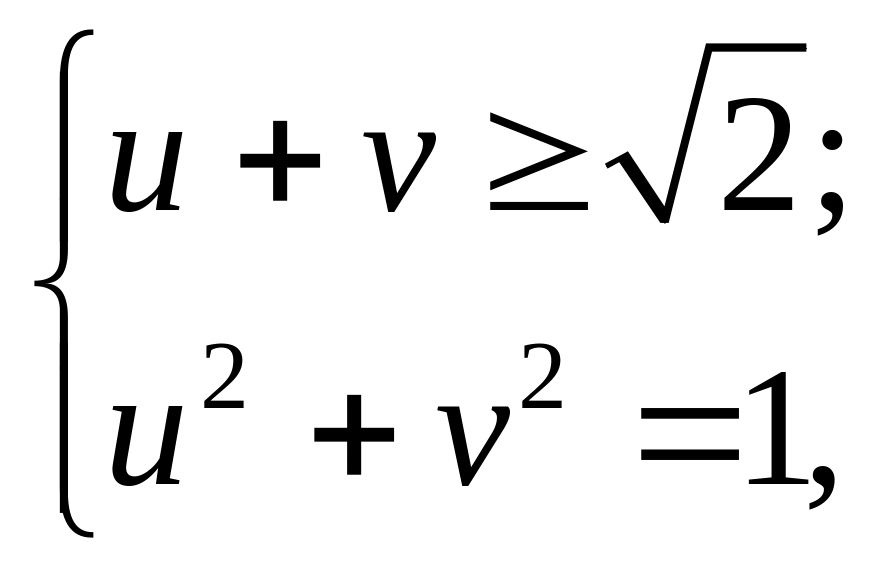графическое решение которой – единственная точка (см. рис. 30).

Каждое из уравнений ,

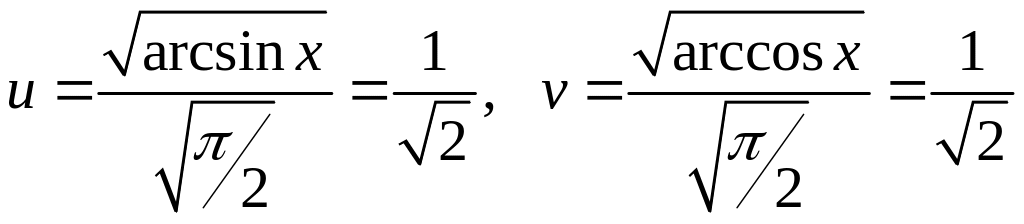Рис. 30

или 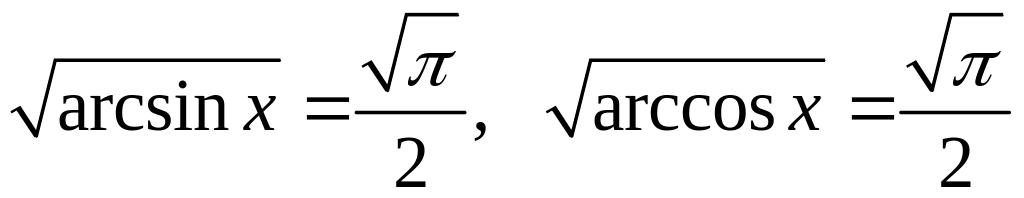дает значение

Ответ.

Задание 19) .

Решение.

Первый способ. .

Решим графически данное неравенство. Строим графики и (см. рис.31).

Точки пересечения графиков можно переписать в виде . Получаем совокупность двойных неравенств

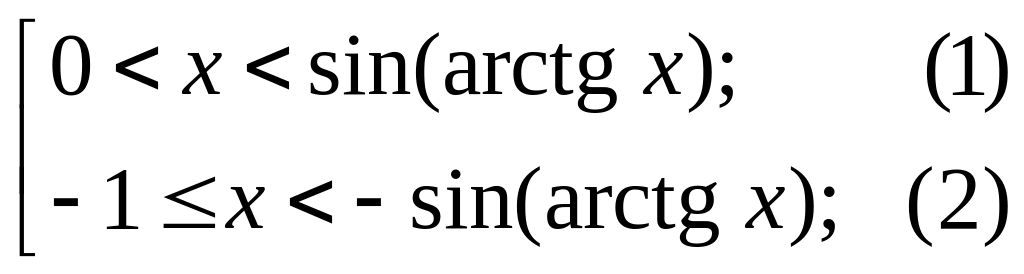
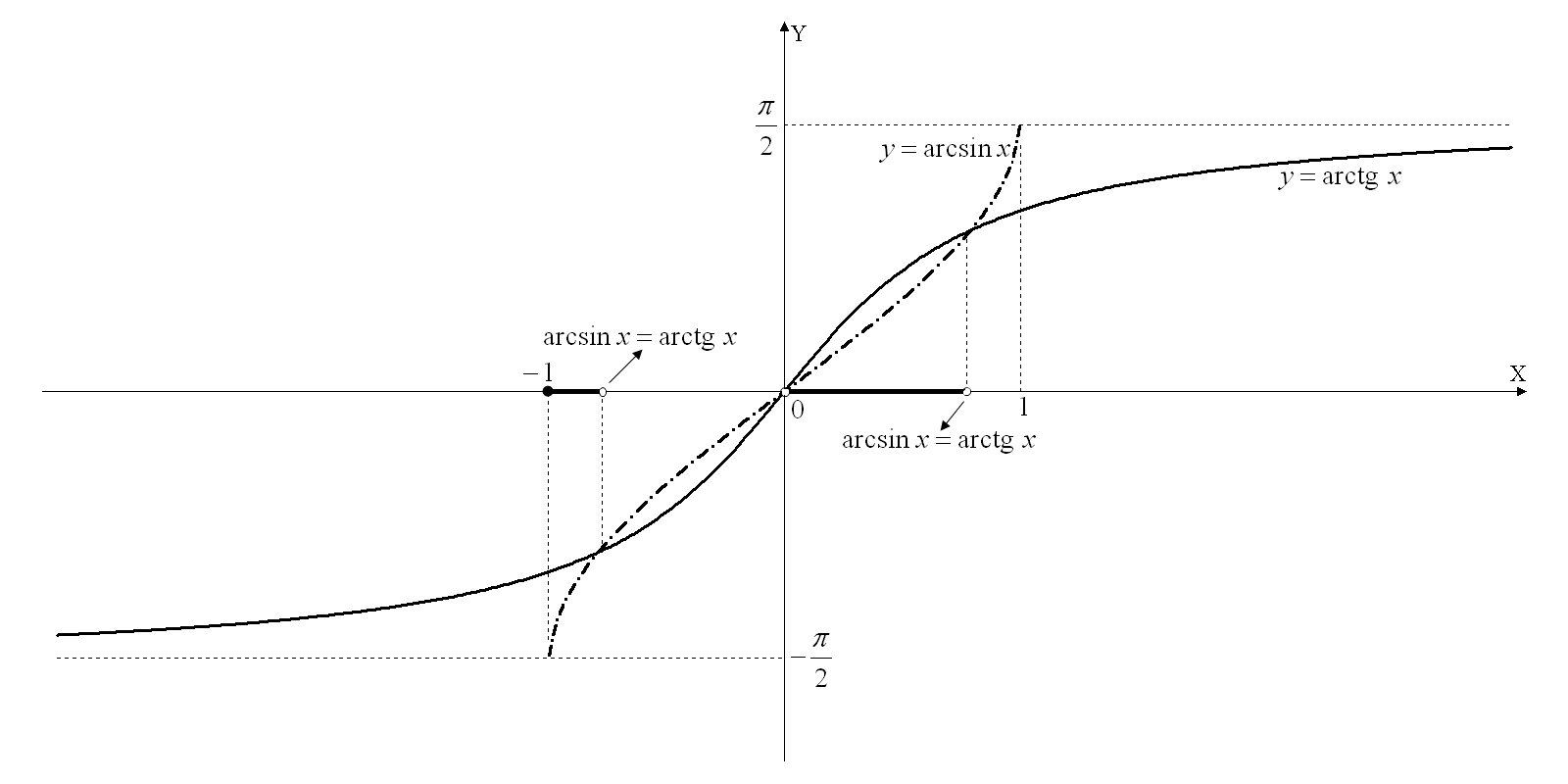Рис.31

Упростим . Пусть , тогда , где .

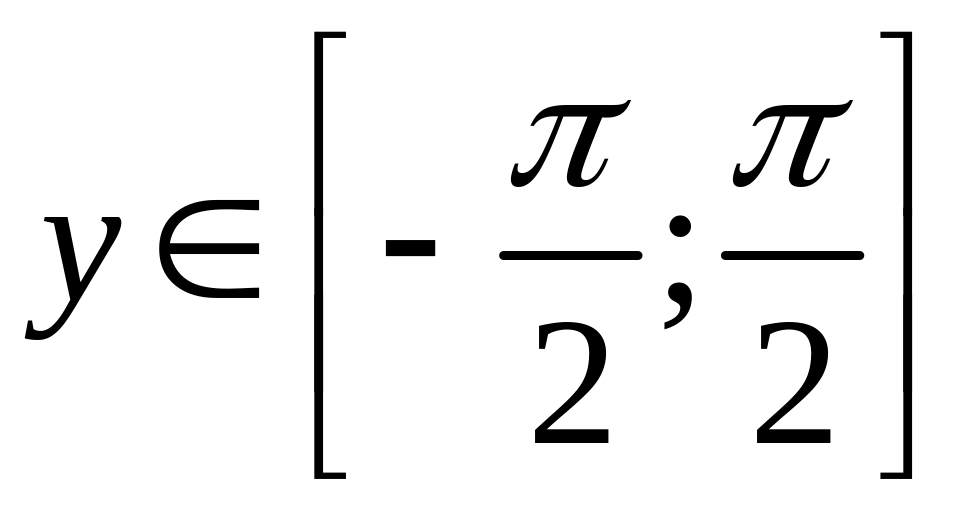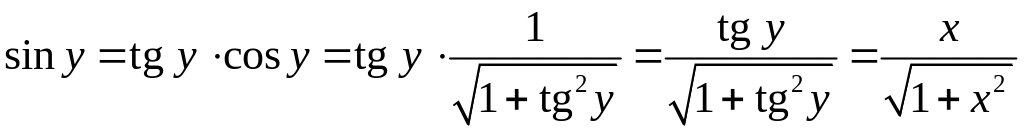. Решим двойное неравенство (1) с учетом того, что :

.

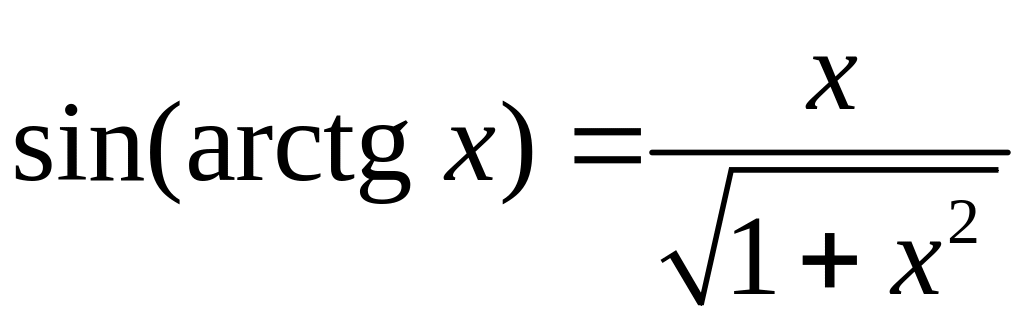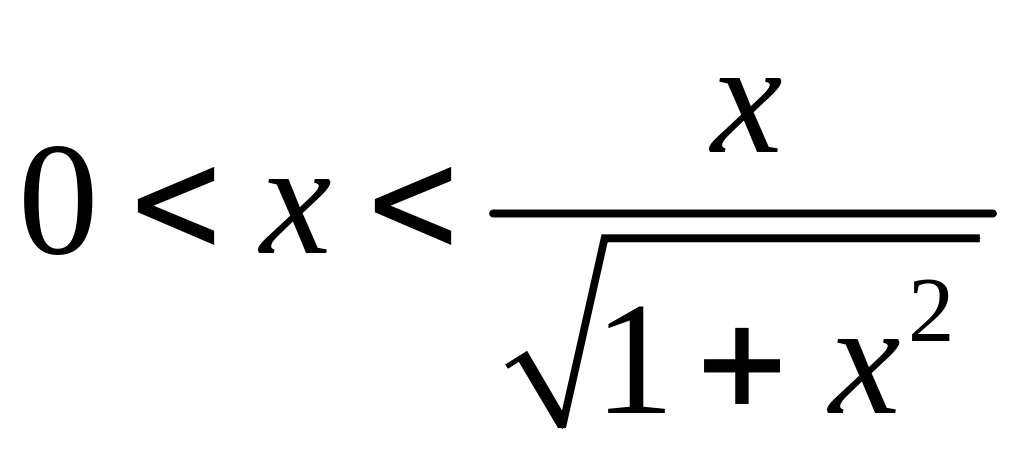Имеем систему

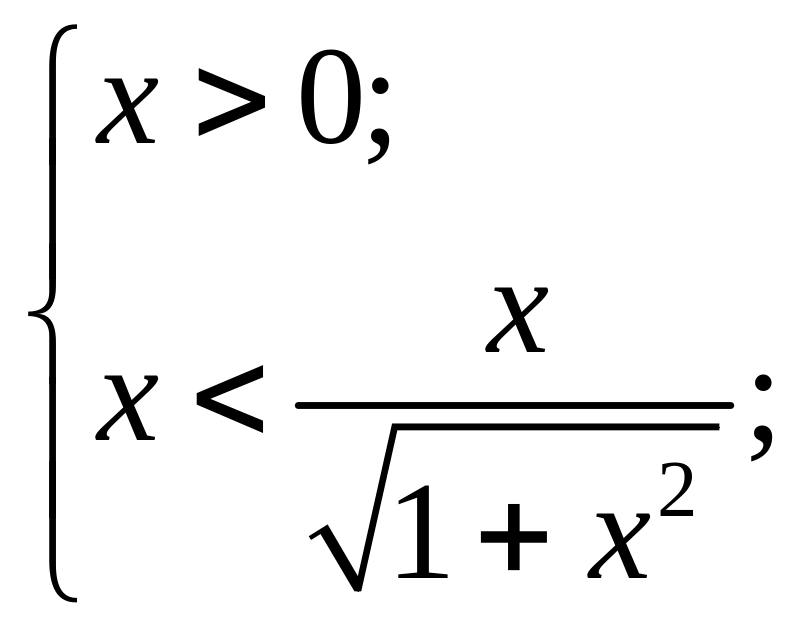
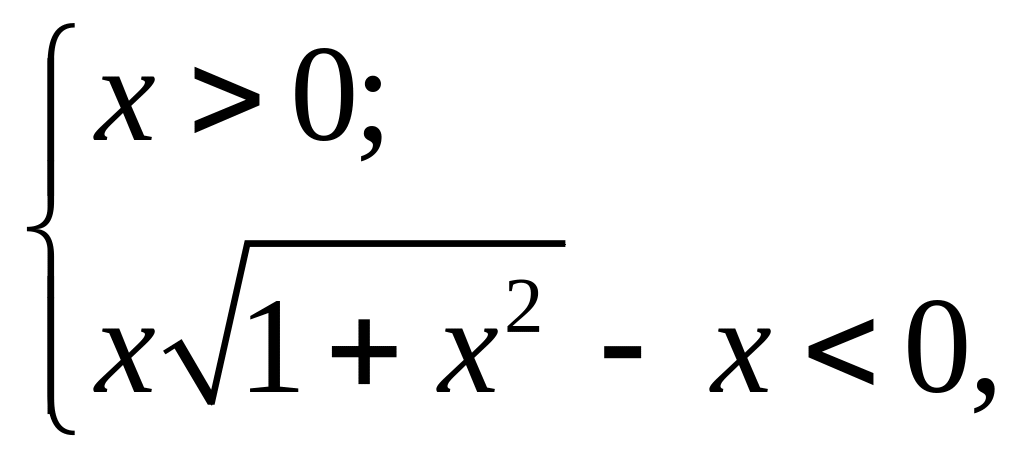
(так как для любого )

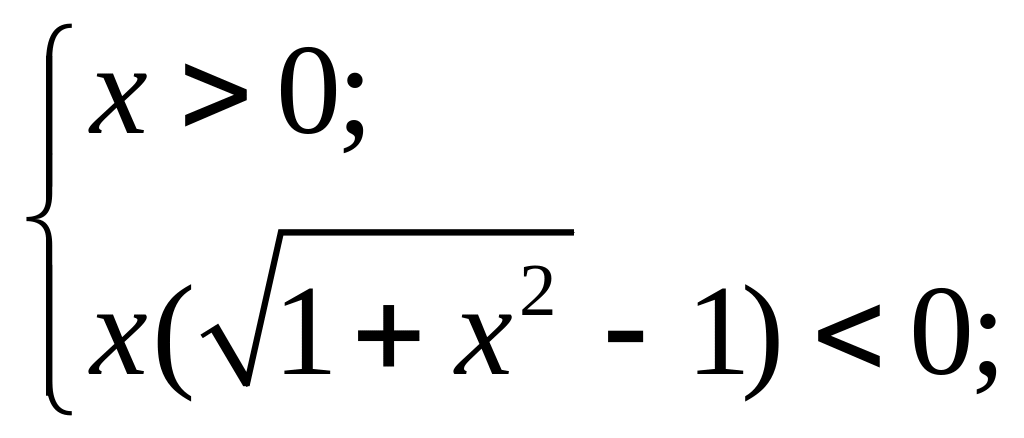
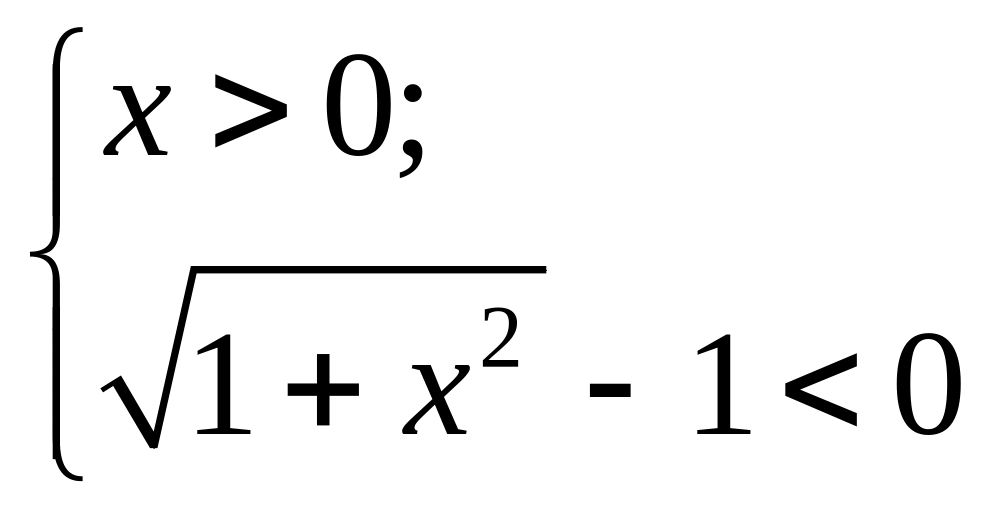
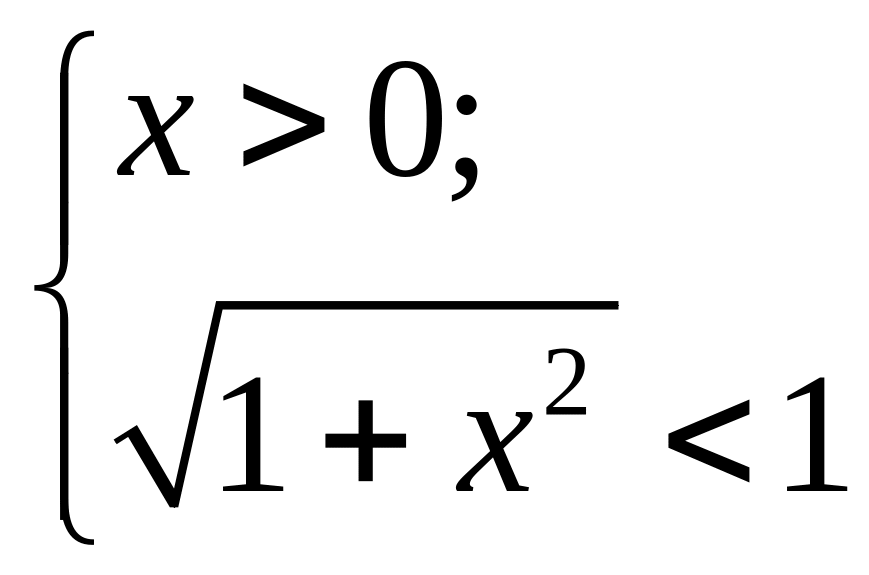
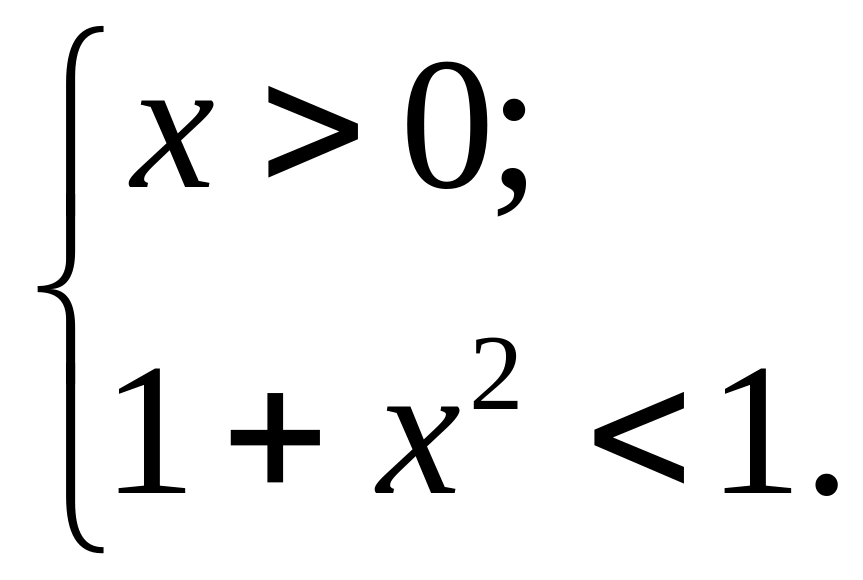
Данная система не имеет решений. Значит неравенство (1) не имеет решения.

Решим двойное неравенство (2) с учетом того, что = :

.

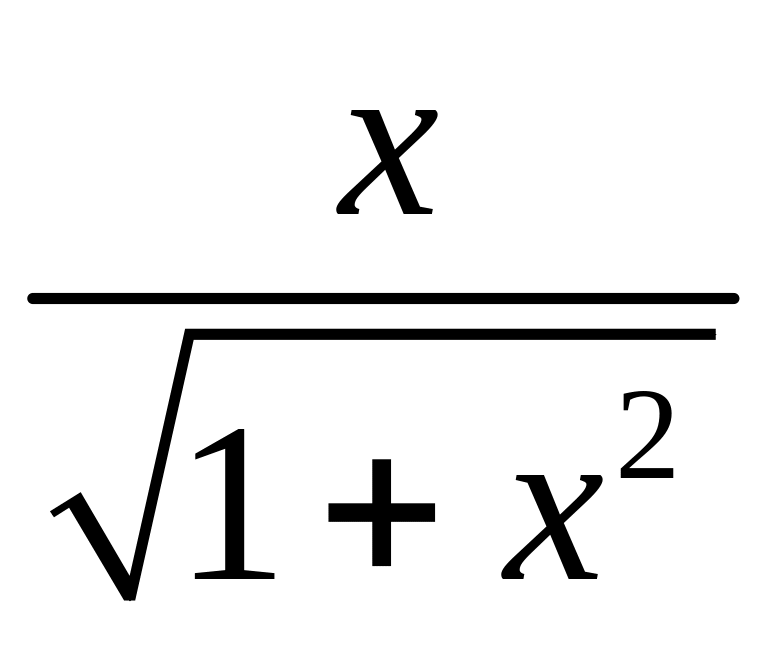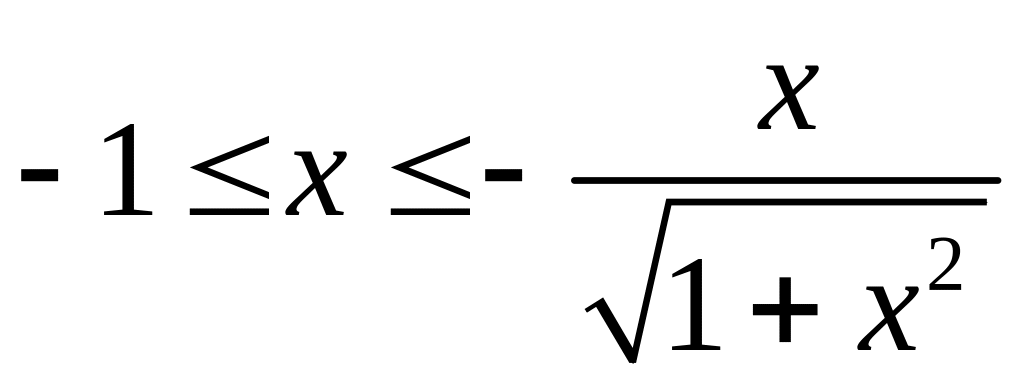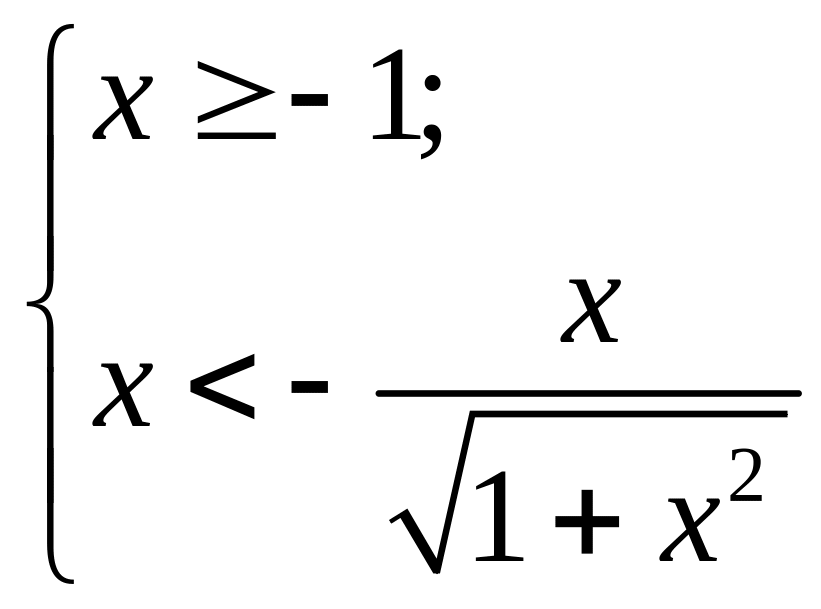
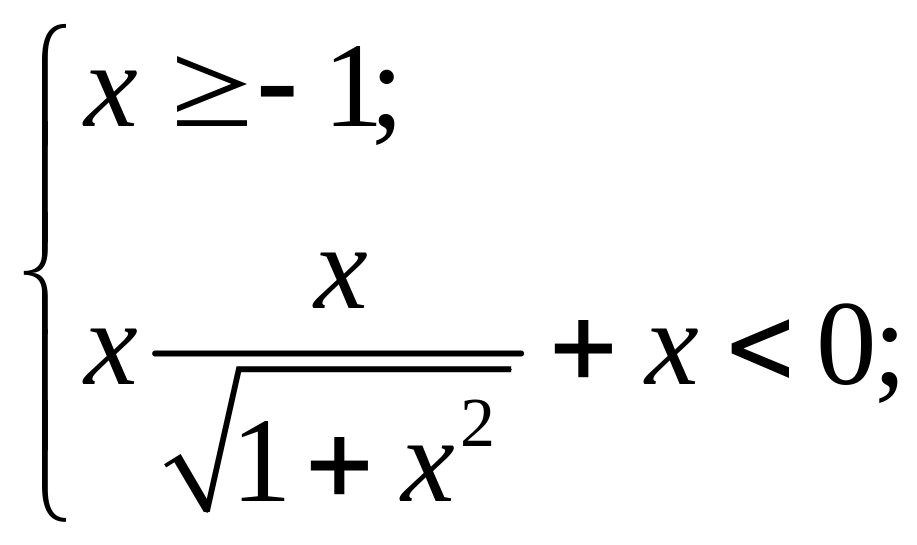
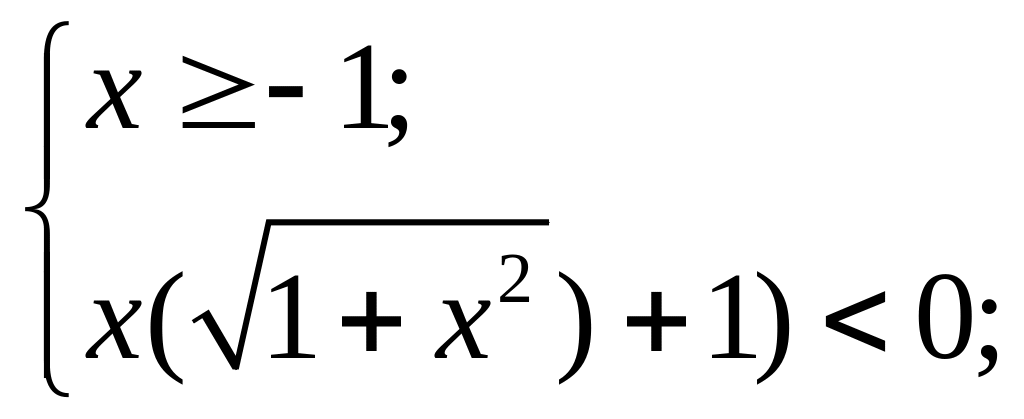
Имеем систему 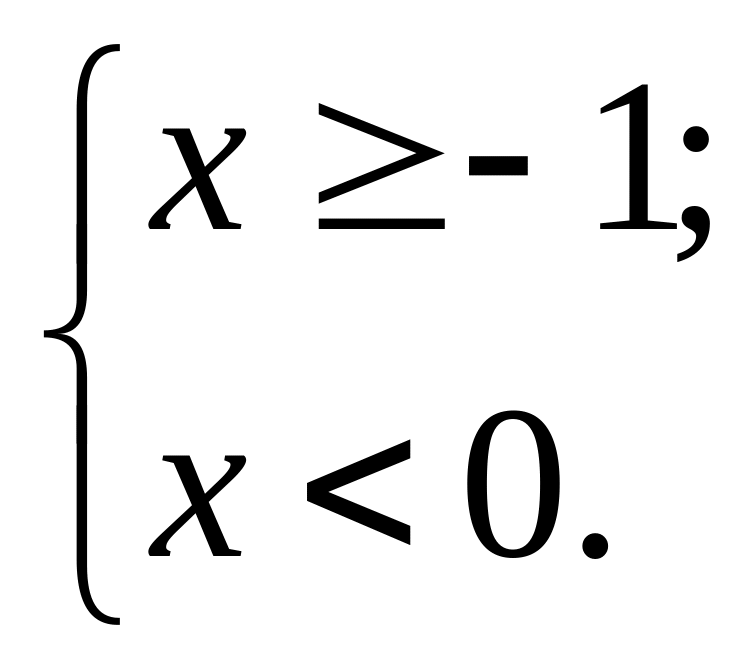(так как ).

Значит, .

Второй способ. .

Область определения неравенства – отрезок . Функции, входящие в неравенство, принимают значение из отрезка , на нём функция монотонно возрастает. Применим её, получим неравенство

,

а так как , то неравенство примет вид

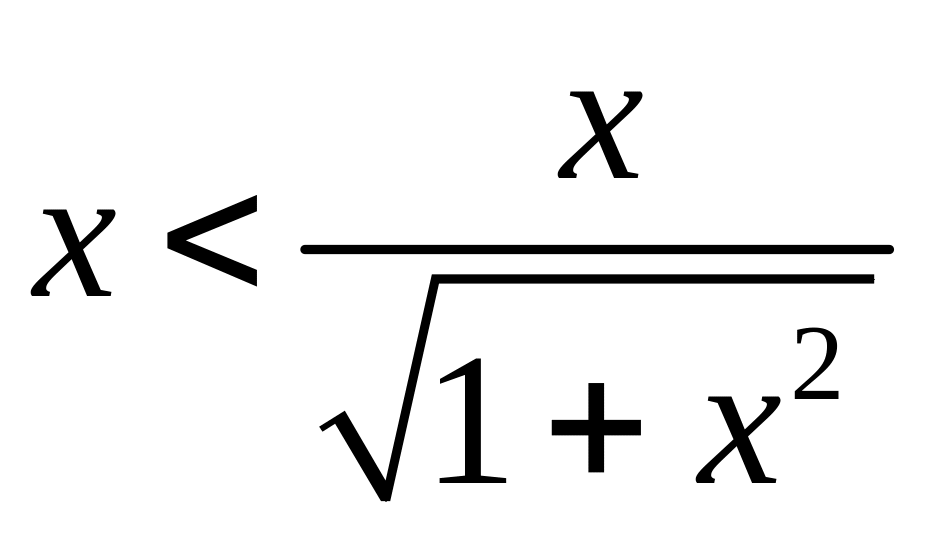, или .

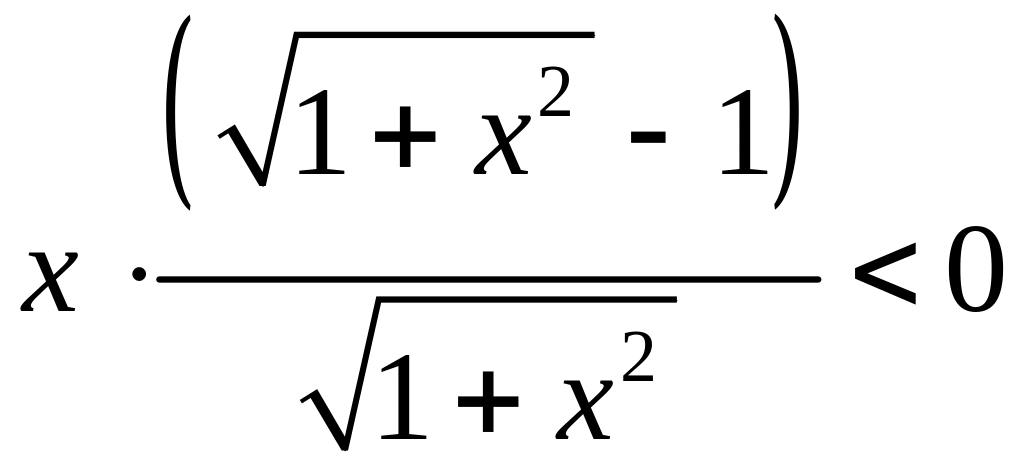Очевидно, что не является решением неравенства, а при и числитель и знаменатель дроби положительны. Следовательно, наше неравенство равносильно , а с учетом ОДЗ имеем .

Третий способ. .

Заметим, что на интервале выполнено , так как . Следовательно, на этом промежутке график функции расположен ниже графика функции . Но при построении графика обратной функции, отображение происходит относительно биссектрисы первого координатного угла, а поэтому график функции уже будет расположен выше графика функции .

А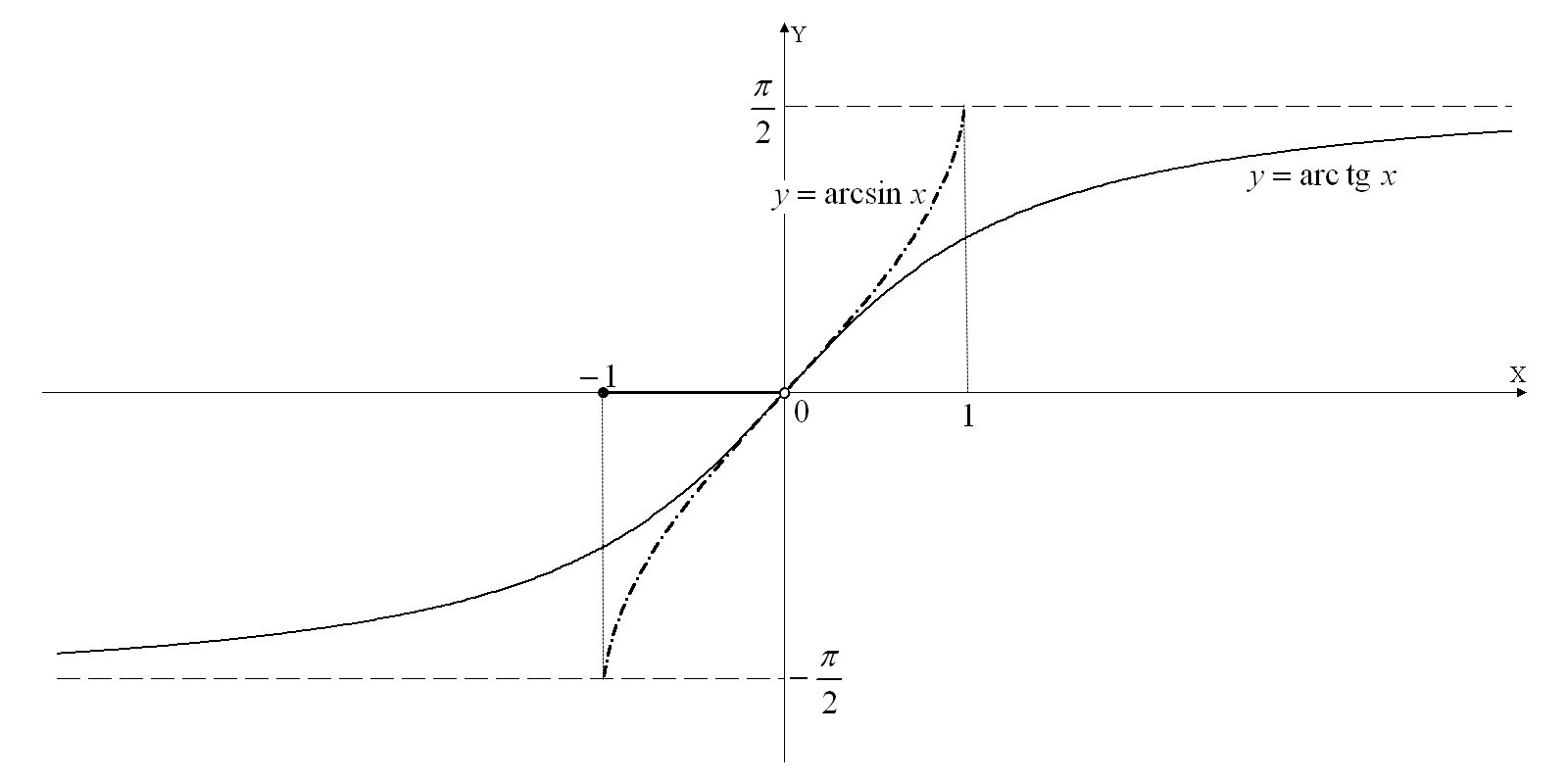 налогично на интервале будет выполнено , а график функции уже будет расположен ниже графика функции .

Рис. 32

Следовательно, рисунок 31 используемый для первого способа решения, неправильный, а правильный (см. рис 32) сразу позволяет дать ответ .

Ответ. .

Задание 20. .

Решение.

Первый способ. .

Построим графики функций и . Точку пересечения перепишем в виде .

Имеем (см. рис. 33).

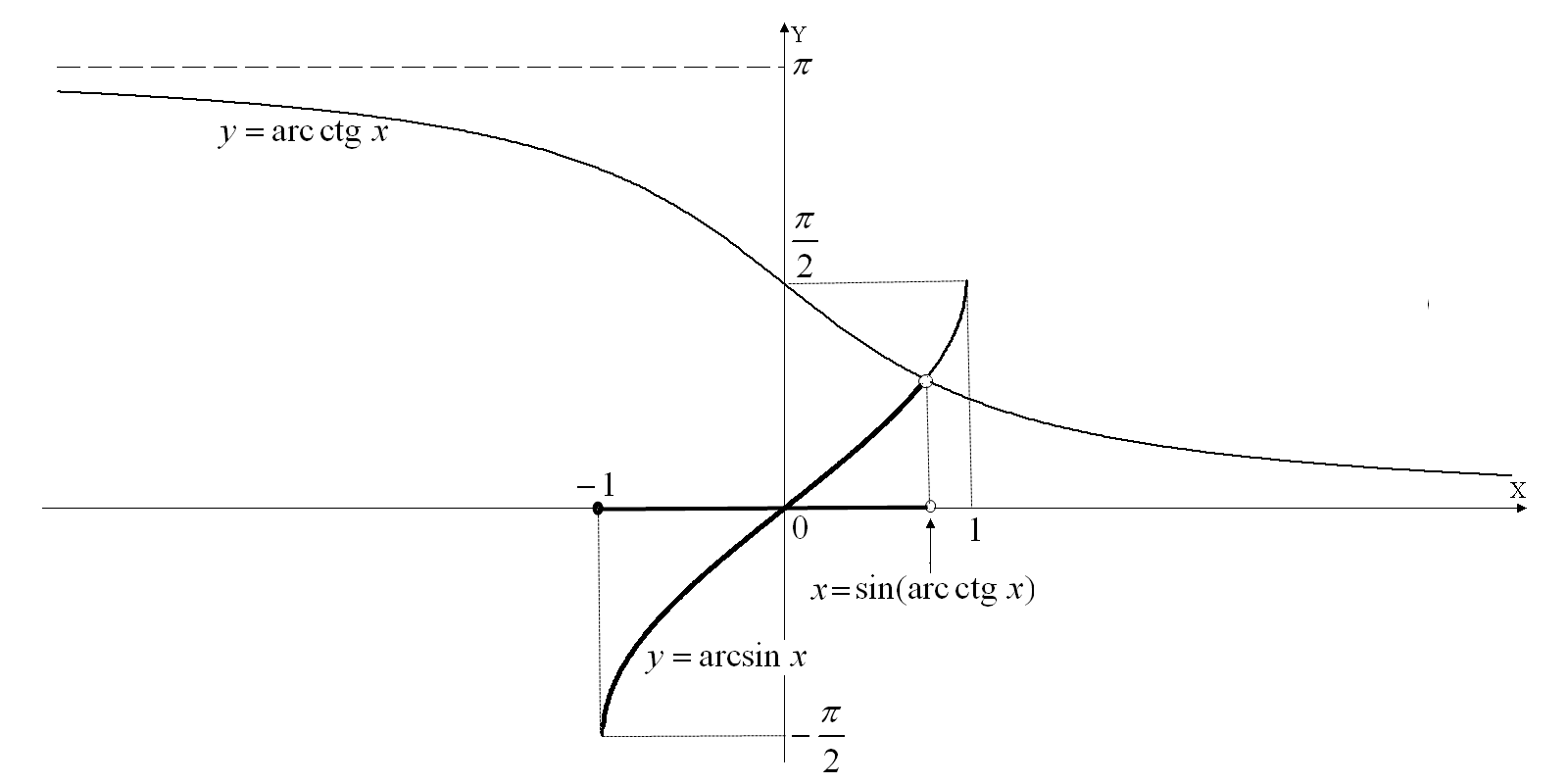Рис.33

Упростим выражение .

Пусть , тогда , где :

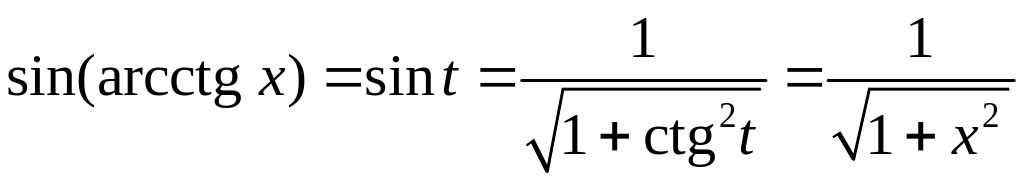. Наш промежуток

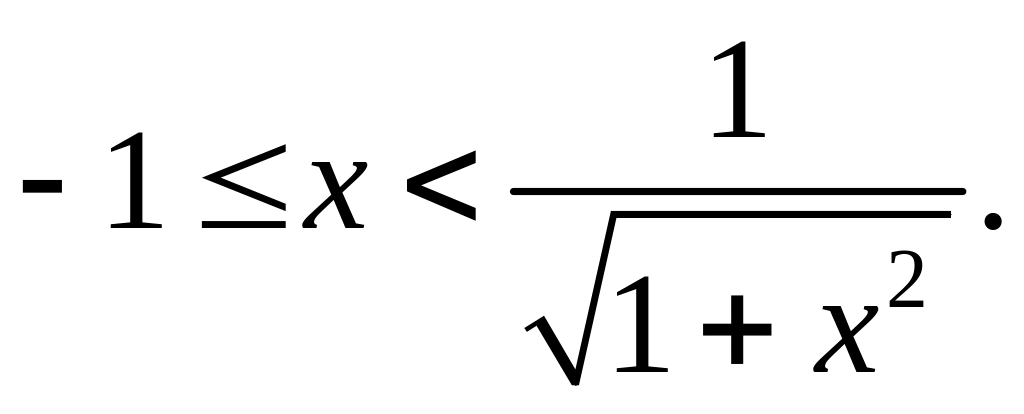
Переходим к системе

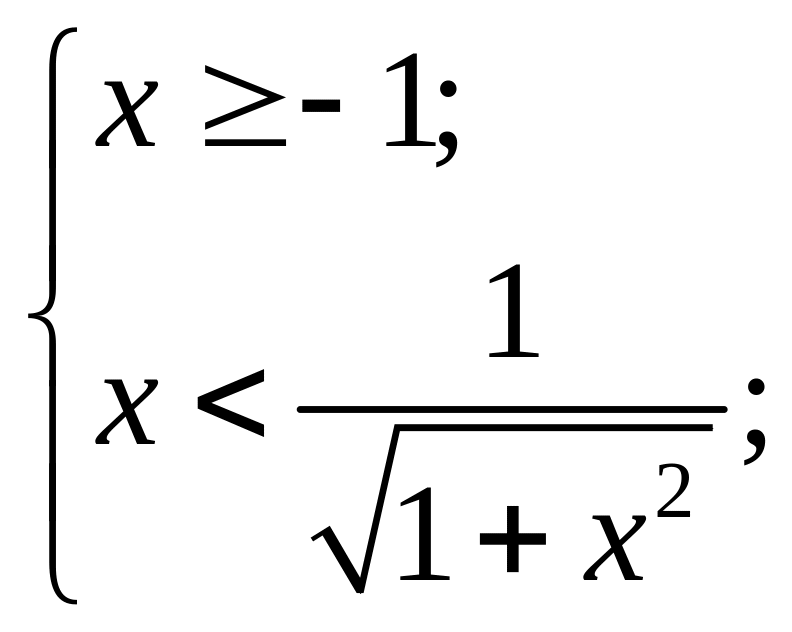
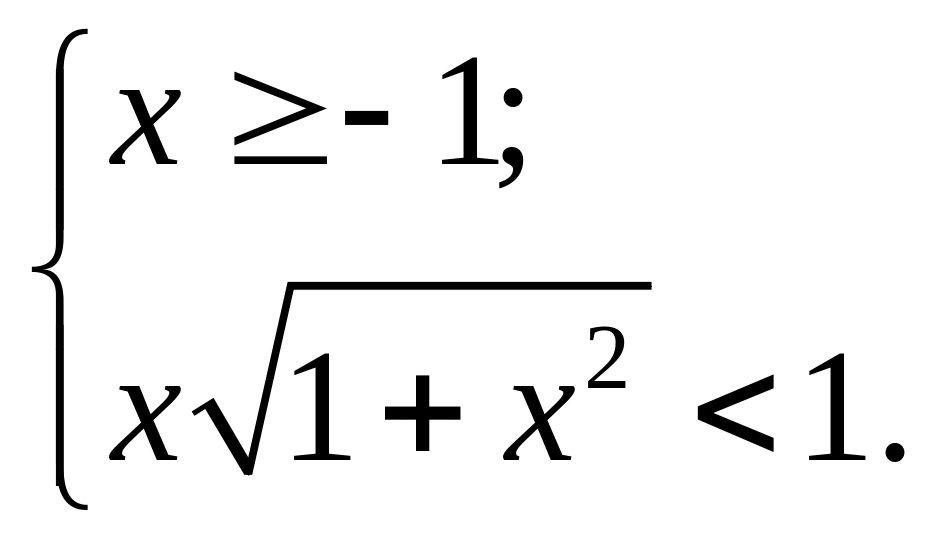
Откуда следует совокупность систем

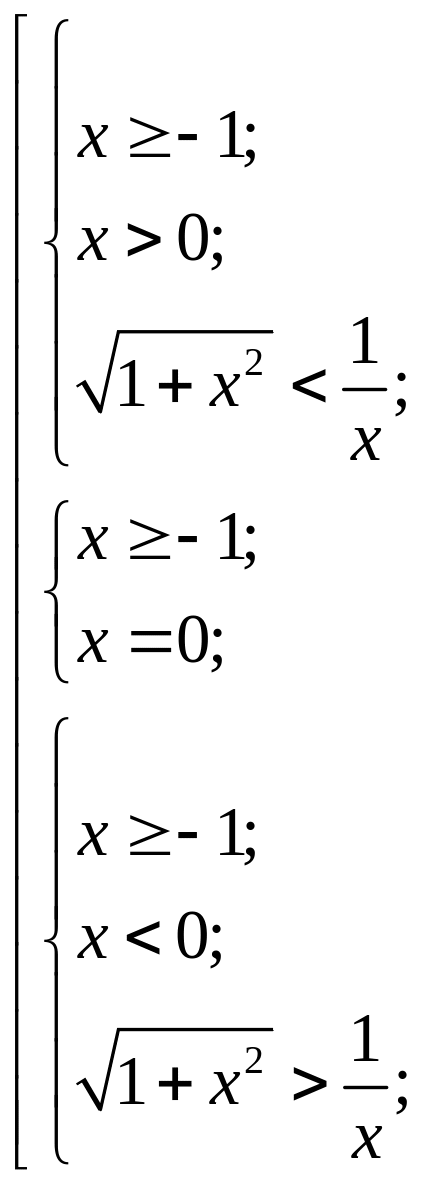
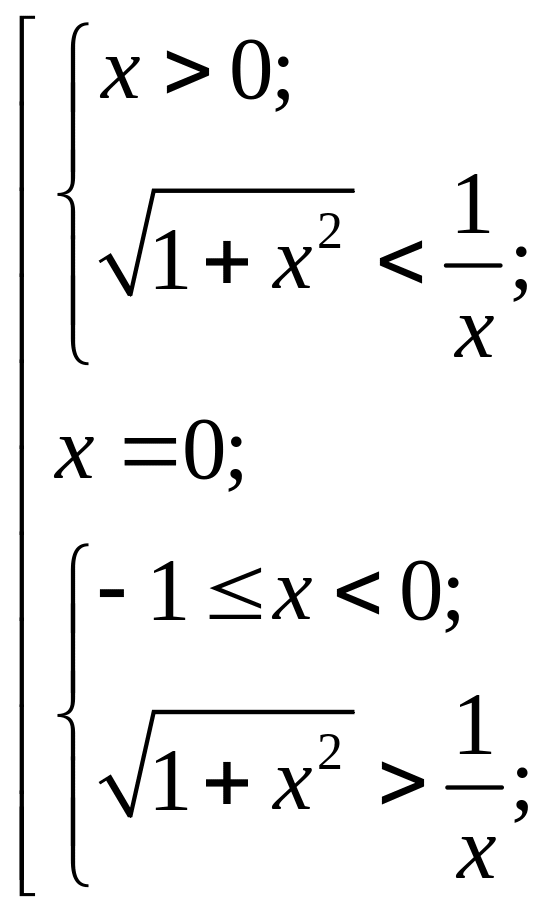
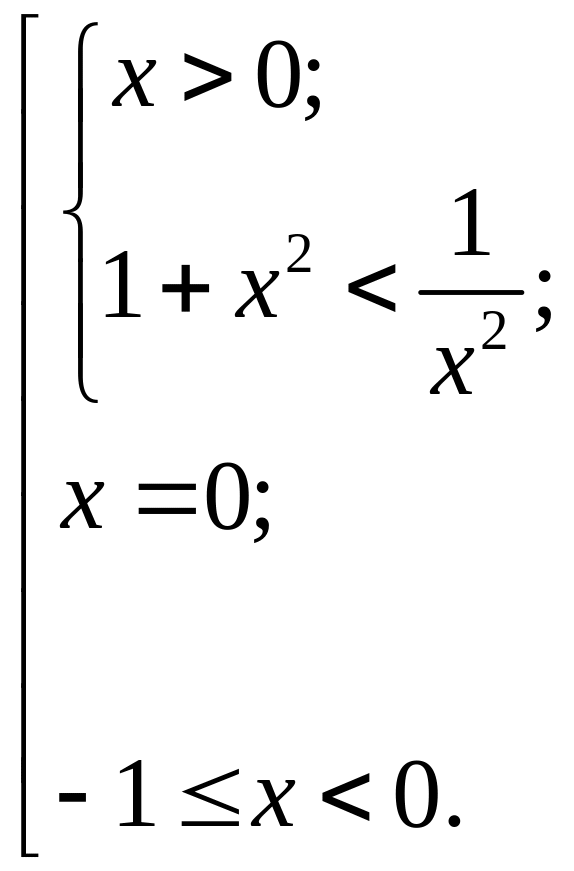
Так как в третьей системе на данном интервале, то справедливо для любого из .

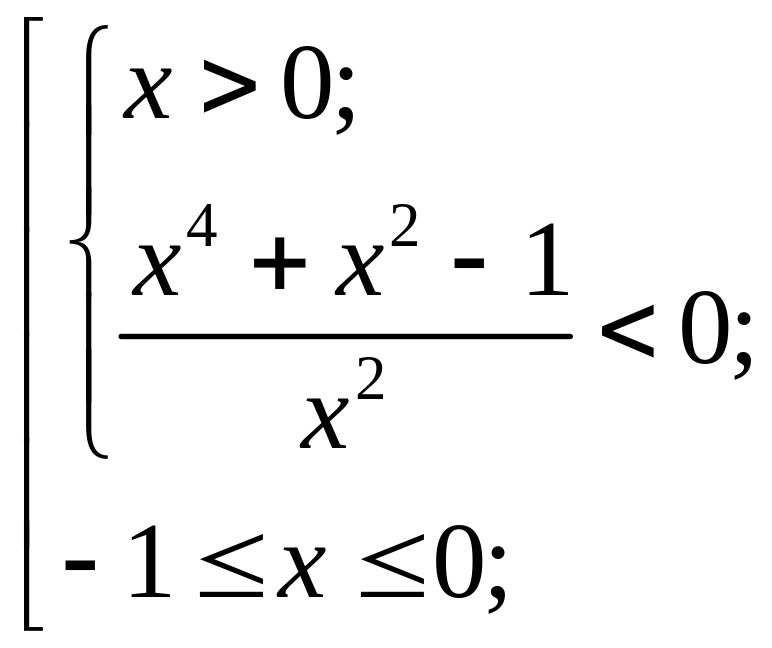
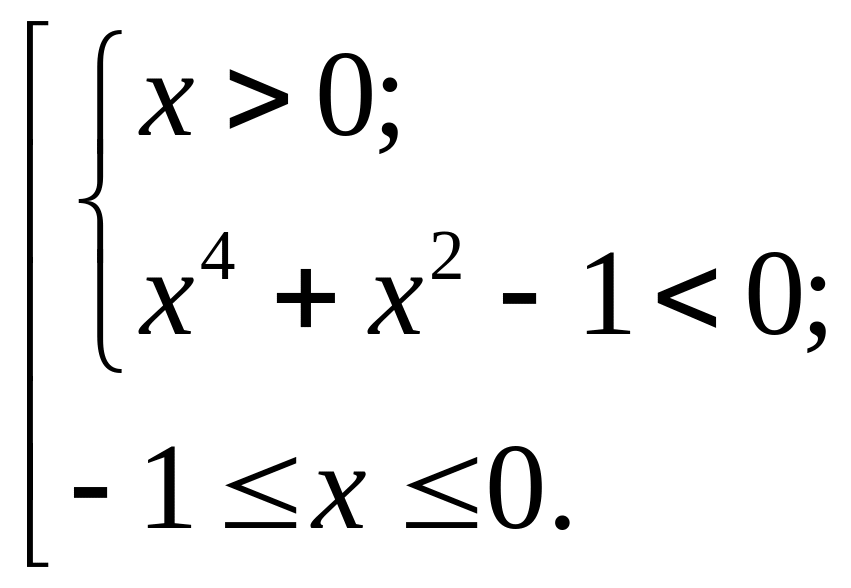
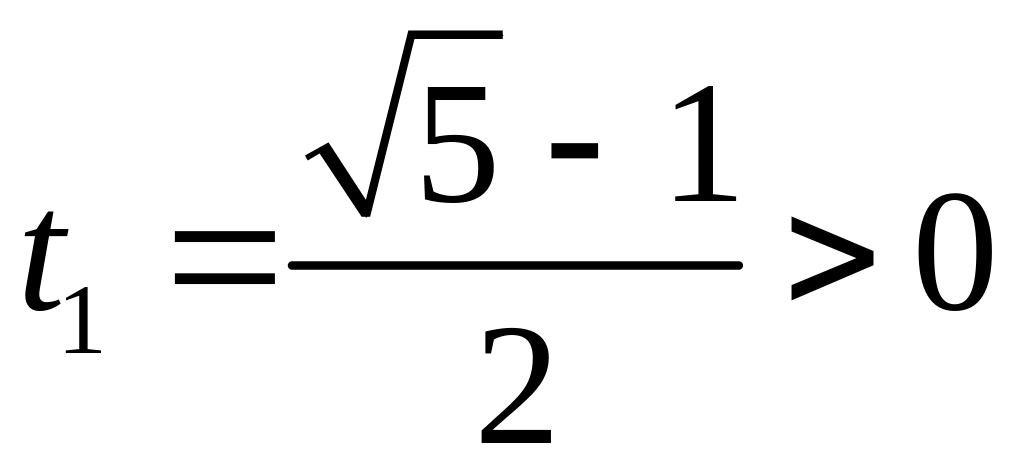
Для решения биквадратного неравенства , найдем корни уравнения , применив замену , тогда 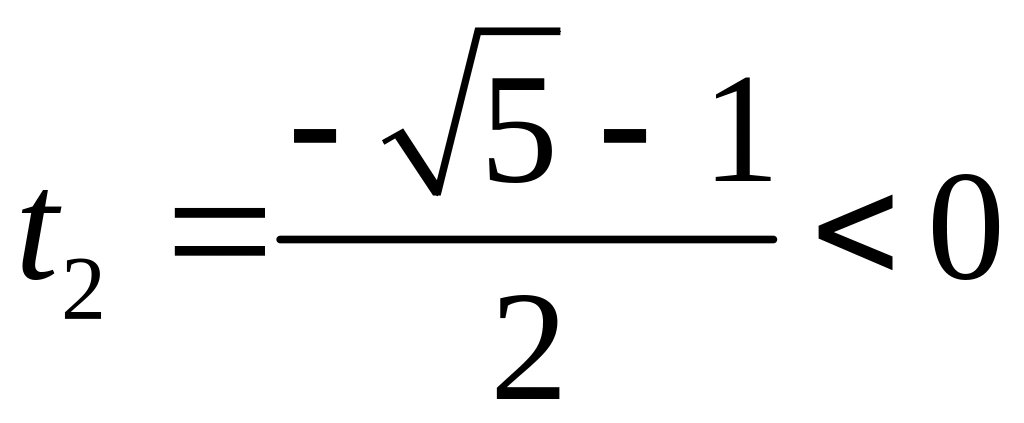. Следовательно ‑ посторонний.

Разложим на множители

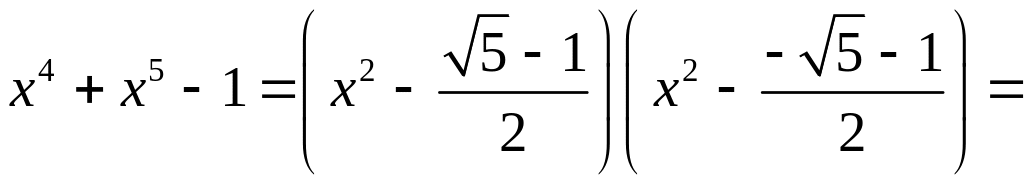
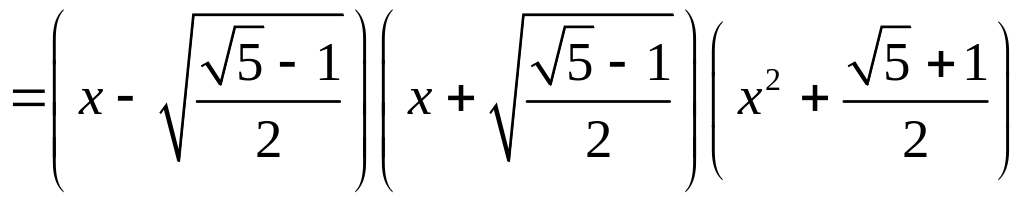
Решим неравенство методом интервалов

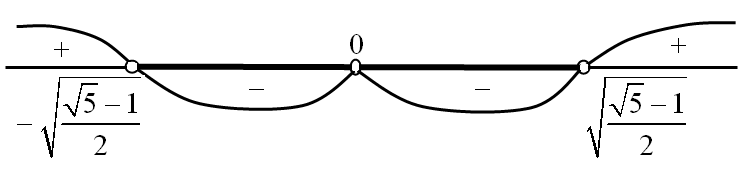
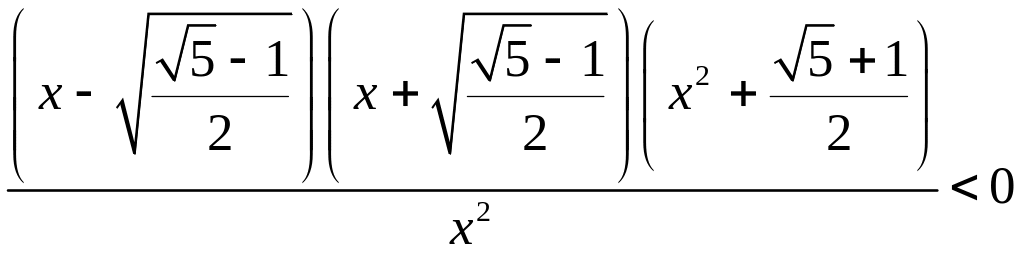. (см. рис. 34).

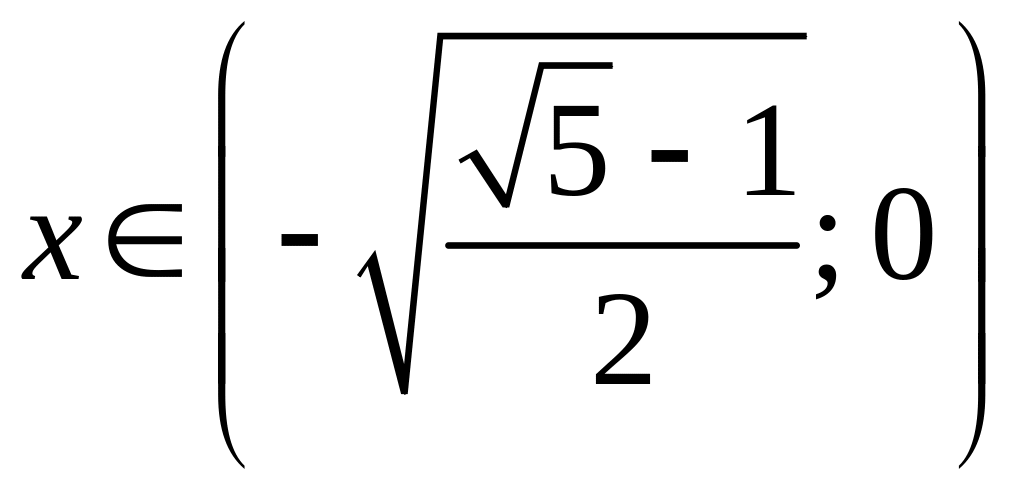
и .

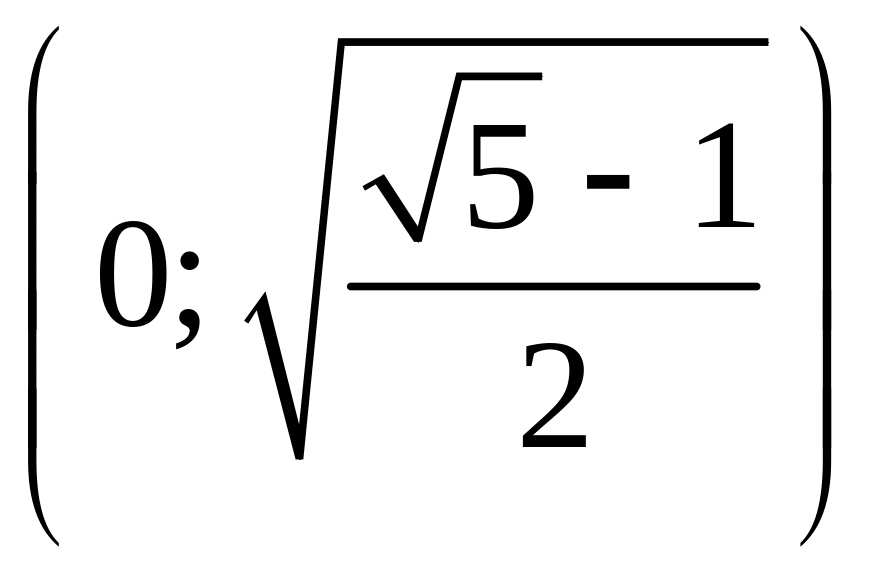Рис.34

С учетом того, что в этой системе , решением является интервал 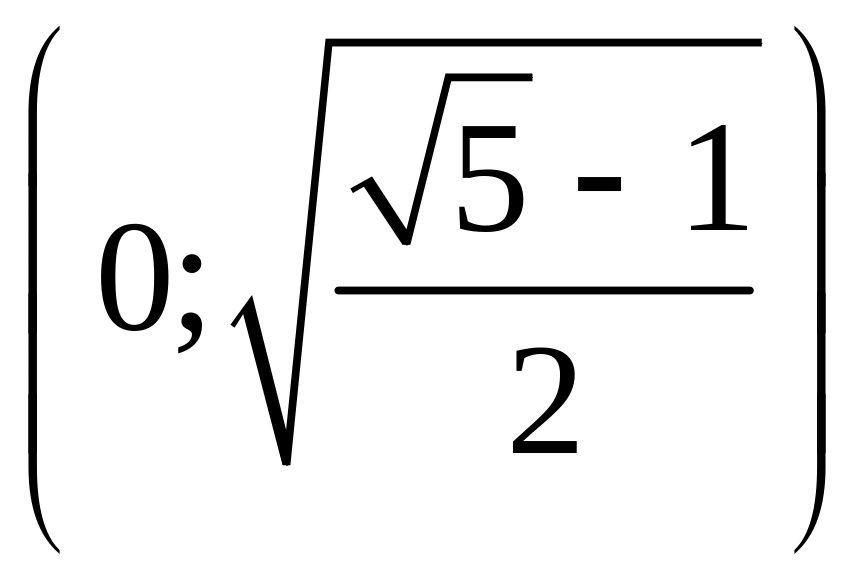. Итак, имеем совокупность

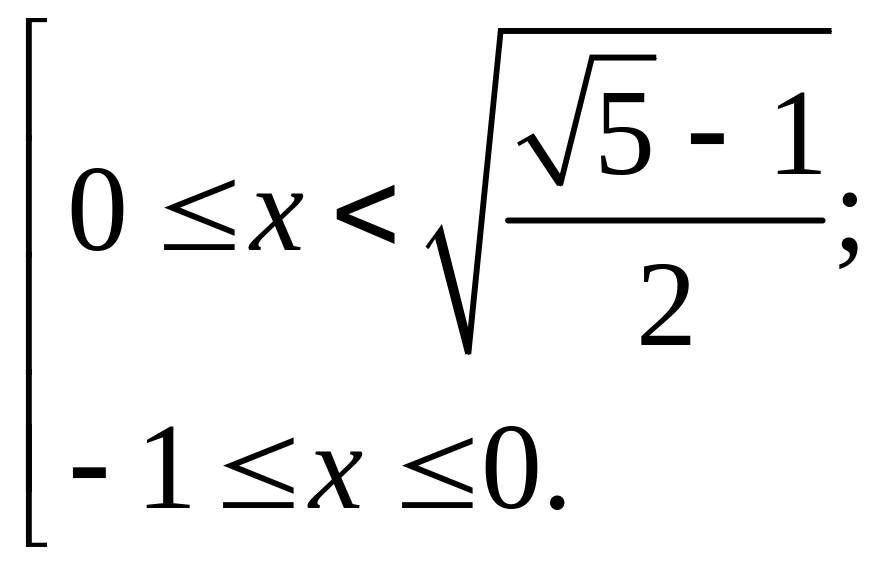
Откуда следует, что .

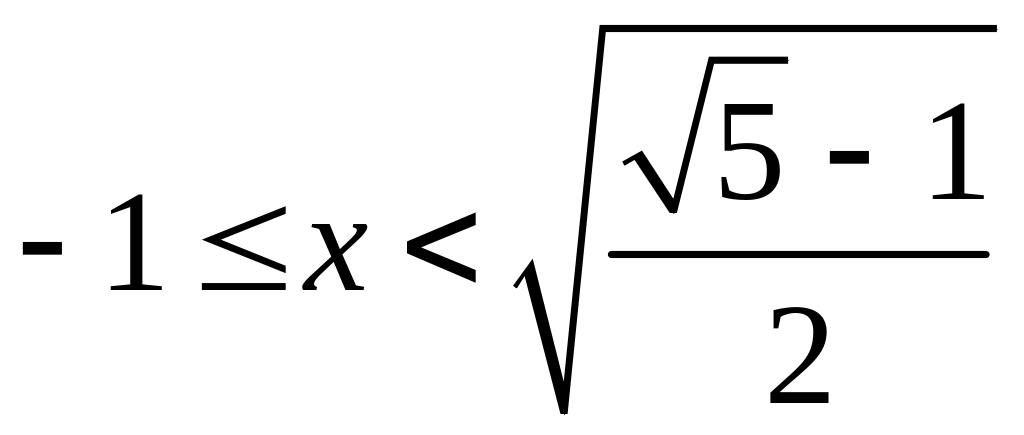Второй способ. .

Область определения неравенства – отрезок . Воспользуемся свойством монотонности. Слева функция возрастает, а справа функция убывает. Графики таких функций если и пересекаются, то только в одной точке , где , а левее от этой точки возрастающая функция меньше. Следовательно, неравенство справедливо на промежутке . Найдем , решив уравнение . Применим функцию :

;

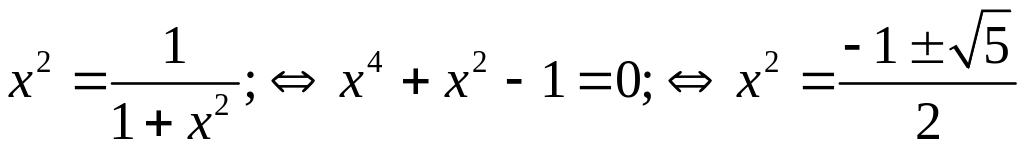. Больше нуля 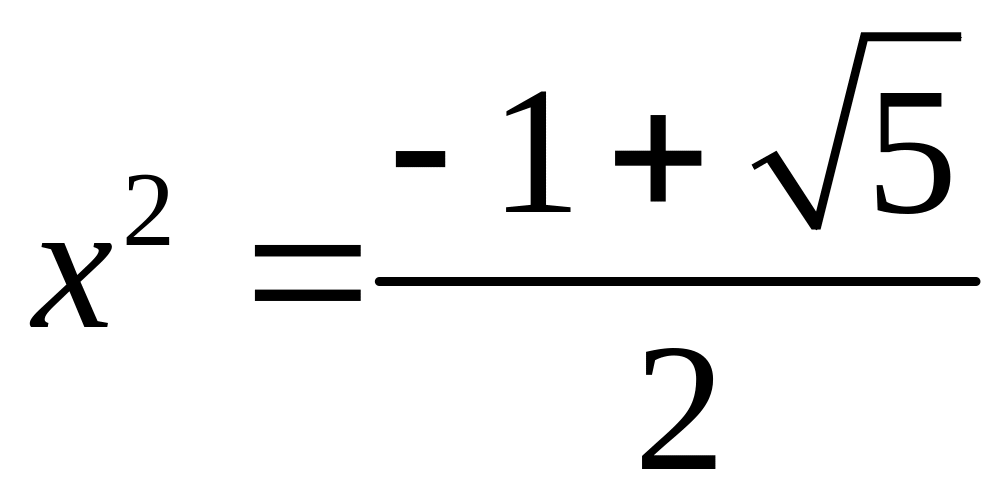; 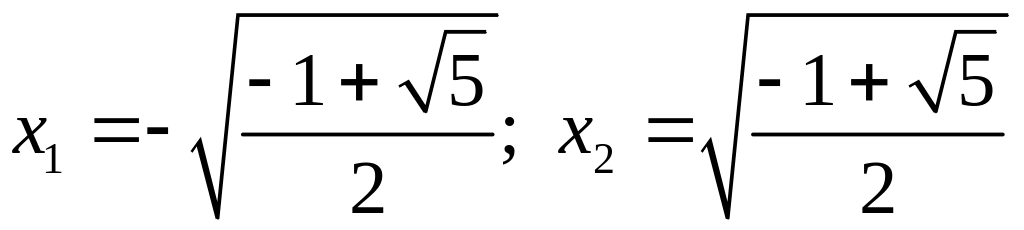. Заметим, что на ОДЗ , следовательно , поэтому , а значит .

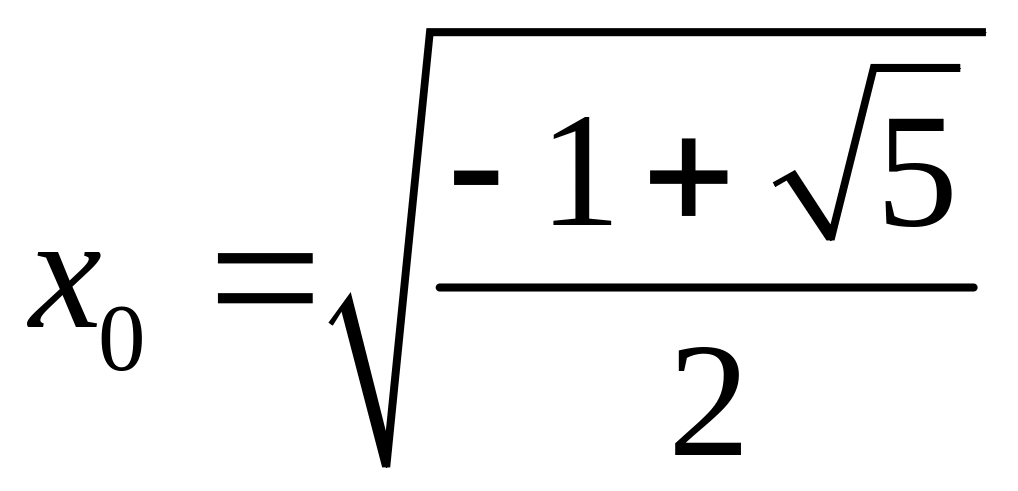Ответ. .

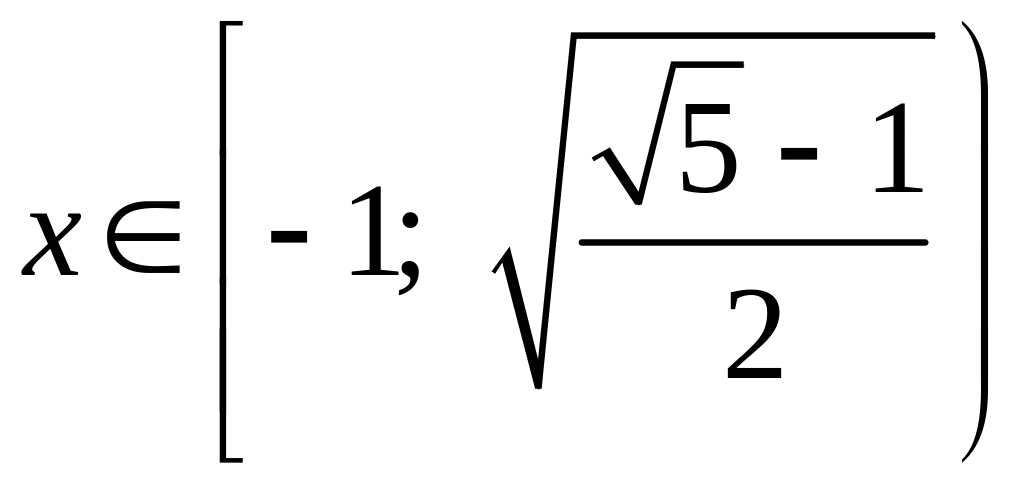Задание 21.

Решение.

Первый способ. Функция ограничена снизу нулем, поэтому функция должна удовлетворять неравенству ; .

При условии обе части неравенства принимают значения из полуинтервала (так ) , а на этом промежутке функция возрастает.