
- •1 Комплексные числа и их геометрическое представление. Предел последовательности, сумма числового ряда
- •5 Геометрический смысл модуля и аргумента производной. Конформные отображения
- •1 3 Определение интеграла и его свойств
- •16 Первообразная аналитической функции. Формула Ньютона – Лейбница
- •17 Интегральное представление логарифма
- •18 Основная формула таф (интегральная формула Коши)
- •23 Оценка коэффициентов ряда Тейлора. Теорема Лиувилля. Основная теорема алгебры многочленов. Понятие кратности корня любой аналитической функции
- •2 4 Теорема единственности аналитической функции
- •26 Ряды Лорана. Разложение аналитических функций в ряд Лорана
- •1 Функцию разложить в ряд Лорана а) в окружности точки , т.Е. По степеням ; б) в кольце в) в кольце
- •28 Вычеты. Основная теорема о вычетах
- •29 Вычисление вычетов
- •30 Примеры вычисления интегралов с помощью вычетов
- •1 Следует усвоить не готовые формулы, а метод их получения.
16 Первообразная аналитической функции. Формула Ньютона – Лейбница
Если
функция
аналитическая в односвязной области
и
фиксированная,
а
переменная точка этой области то интеграл
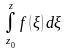 по теореме 1 параграфа 15 не зависит от
кривой интегрирования и, следовательно,
является функцией от
.
Обозначим
по теореме 1 параграфа 15 не зависит от
кривой интегрирования и, следовательно,
является функцией от
.
Обозначим
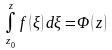
Теорема
1 При названных выше условиях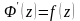 .
.
Доказательство
Для любого
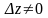 найдем соответствующее приращение
функции:
найдем соответствующее приращение
функции:

В
связи с независимостью интеграла от
кривой можно считать его взятым по
отрезку
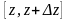 прямой
прямой
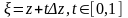 .
Формула
.
Формула
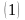 параграф 11 позволяет свести его к
определенному интегралу. Так как
параграф 11 позволяет свести его к
определенному интегралу. Так как
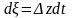 ,
,
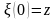 ,
,
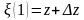 ,
то
,
то
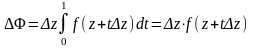 где
где
 .
В последнем равенстве мы применим
интегральную теорему о среднем. Деля
полученное равенство на
и переходя к пределу при
.
В последнем равенстве мы применим
интегральную теорему о среднем. Деля
полученное равенство на
и переходя к пределу при
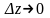 ,
получим, в силу непрерывности
в точке
,
,
получим, в силу непрерывности
в точке
,

Заметим, что аналитичность функции и неодносвязность в процессе доказательства понадобилась лишь дважды: 1 для установления независимости интеграла от пути интегрирования и 2 для непрерывности функции . Поэтому, не меняя основы приведенного доказательства, мы по сути дела получим более общую теорему, которая пригодится нам в будущем:
Теорема 2 Если функция непрерывна в произвольной области и если в этой области интеграл от функции не зависит от пути интегрирования, то функция
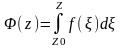 является
аналитической в
и
является
аналитической в
и
Определение
Пусть
– область. Если
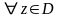
 ,
то
,
то
 называется первообразной функции
в
.
называется первообразной функции
в
.
Теорема 3 Все первообразные для данной непрерывной функции отличаются друг от друга на постоянную.
Доказательство
Пусть в области
функция
имеет две первообразные
 и
и
 .
Обозначим
.
Обозначим
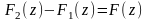 .
Очевидно, что
.
Очевидно, что
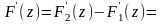
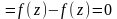 и
и
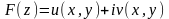 – функция аналитическая в
.
Кроме того
– функция аналитическая в
.
Кроме того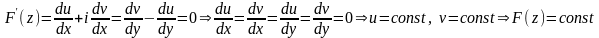 Теорема
4 (Формула Ньютона-Лейбница) Если
Теорема
4 (Формула Ньютона-Лейбница) Если
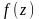 непрерывна в
и интеграл от нее не зависит от пути
интегрирования (например, если
аналитическая в односвязной области
),
и
– любая ее первообразная в области
,
то
непрерывна в
и интеграл от нее не зависит от пути
интегрирования (например, если
аналитическая в односвязной области
),
и
– любая ее первообразная в области
,
то

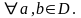
Доказательство
Рассмотрим
 .
Тогда:
.
Тогда:
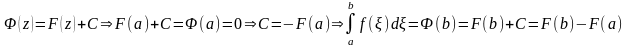
Пример

17 Интегральное представление логарифма
Рассмотрим
интеграл
 ,
где любая точка, отличная от нуля.
Аналитичность подынтегральной функции
нарушается только в точке
.
Подсчитаем этот интеграл по любому
пути, соединяющему точки
и
,
но не пересекающему отрицательную
полуось
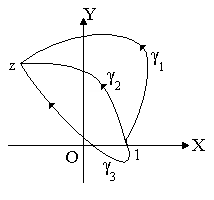
(Рисунок.25). Очевидно, что все пути можно
поместить в односвязную область, не
содержащую точку
и, следовательно, интегралы по ним будут
равны. В качестве наиболее удобного
пути для подсчета интеграла выберем
путь, изображенный на рисунок 26, где
,
где любая точка, отличная от нуля.
Аналитичность подынтегральной функции
нарушается только в точке
.
Подсчитаем этот интеграл по любому
пути, соединяющему точки
и
,
но не пересекающему отрицательную
полуось
(Рисунок.25). Очевидно, что все пути можно
поместить в односвязную область, не
содержащую точку
и, следовательно, интегралы по ним будут
равны. В качестве наиболее удобного
пути для подсчета интеграла выберем
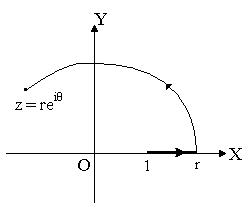
путь, изображенный на рисунок 26, где
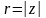 ,
а путь из отрезка
,
а путь из отрезка
 оси
и дуги окружности. Если
оси
и дуги окружности. Если
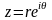 , то уравнение дуги окружности имеет
вид:
, то уравнение дуги окружности имеет
вид:
![]()
![]()
![]() ,
где
,
где

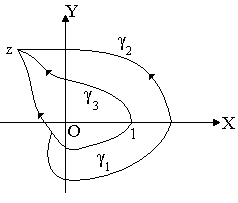
Допустим
теперь, что путь интегрирования пересекает
отрицательную действительную полуось
один раз (Рисунок 27), например
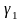 или
или
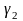 .
Проведем
,
не пересекающую полуось
.
Тогда (см. пример 3 параграф 14)
.
Проведем
,
не пересекающую полуось
.
Тогда (см. пример 3 параграф 14)
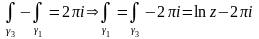

Если кривая пересекает отрицательную полуось раз, то очевидно, что

где означает количество пересечений отрицательной полуоси, понимаемое в алгебраическом смысле, т.е. с соответствующим знаком. Итак, рассматривая данный интеграл по всевозможным путям, мы получим все возможные значения многозначного логарифма .
