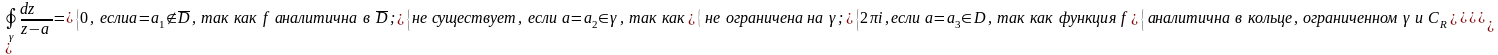1 3 Определение интеграла и его свойств

П усть 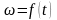произвольная функция, определённая на дуге 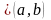кривой Жордана 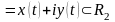. Разобьём на произвольных частей точками 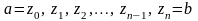. Обозначим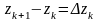 , где 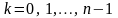. Затем для всякого выберем по произвольной точке 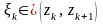и составим интегральную сумму .

Обозначив 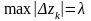, перейдём к пределу при 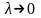, т.е. при условии неограниченного измельчения дуги .

Определение Если существует предел интегральной суммы σ, не зависящий от разбиения и от отмеченных точек , то он называется интегралом по дуге от функции и обозначается .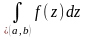

Обозначим 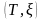разбиение с отмеченными точками , сформулируем уточнённое определение предела интегральной суммы:

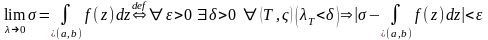
Какие же условия достаточно наложить на дугу и на функцию, чтобы обеспечить существование интеграла? Чаще всего используется следующая теорема:

Теорема Если функция непрерывна на кусочно-гладкой кривой , то существует.

Доказательство Введём обозначение , 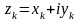, , 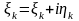. Тогда

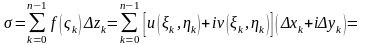
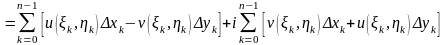
Полученные, суммы являются интегральными для известных нам составных криволинейных интегралов от функций действительных переменных. Эти функции и непрерывны ввиду непрерывности и, в силу известной теоремы существования криволинейных интегралов, предел правой части (а, значит, и предел 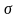) существует. Переходя к пределу, получим не только существование , но и его выражение через криволинейные вещественные интегралы:

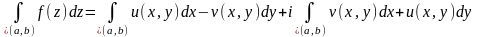(1)

Замечание Если это отрезок действительной оси _, а функция принимает действительные значения, то введенный интеграл совпадает с обычным интегралом Римана от функции действительной переменной.

14 Основные свойства и вычисление интегралов

В дальнейшем будем предполагать, что для рассматриваемых функций и дуги выполняются условия теоремы предыдущего параграфа. Это обеспечивает существование длины дуги и любой ее частичной дуги и существование интегралов. Тогда, опираясь на соответствующие свойства криволинейного интеграла, легко получить следующие свойства комплексных интегралов:

1⁰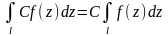

2⁰

₃⁰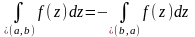

_4⁰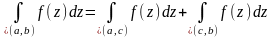

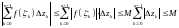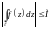5⁰(оценка интеграла) Так как кривая кусочно-гладкая, то она, имеет длину и, так как она является компактом, то . Отсюда (дл. ). Переходя к пределу, получим важную оценку интеграла: (дл. )

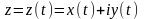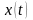Формула (1) параграфа 13 сводит вычисление комплексного интеграла к вычислению криволинейных интегралов. Но эти последние легко сводятся к определённым интегралам. Удобнее было бы эту связь выявить непосредственно. Предположим, что – гладкая кривая , т.е. и имеют непрерывные производные в 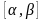, где 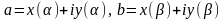. Тогда, сводя (1) параграфа 13 к определённому интегралу, получим:

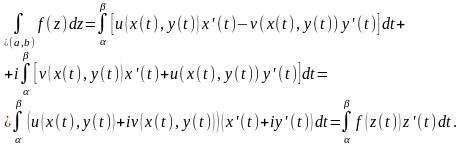(1)

Здесь справа стоит определённый интеграл от комплексной функции действительной переменной .

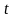Примеры

1 Вычислить ,где – контур треугольника (Рисунок 21).

В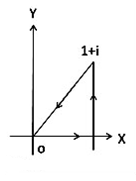 ычислим сначала интеграл по трём гладким частям кусочно-гладкого контура.

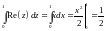
.Рассмотрим 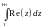. Здесь уравнение линии или 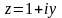, переменная интегрирования , .

.

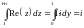У

Рис.21

равнение третьего участка , т.е. , :

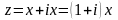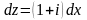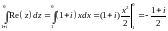. Итак, .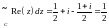

Неравенство нулю интеграла по замкнутому контуру говорит о том, что интегралы от до точки зависят от пути, соединяющего эти точки.

2 Вычислить 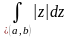где – дуга окружности .

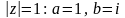Первый способ: Уравнение дуги в прямоугольных координатах: 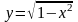, т.е. , . .

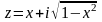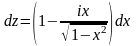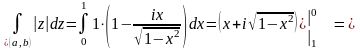
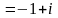Второй способ: Уравнение дуги в полярных координатах: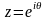 , где 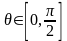, , 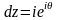подставляя в интеграл, получим:

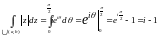
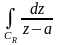1. где – окружность радиуса с центром в точке .

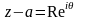
Уравнение : т.е. 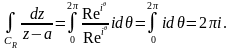При -кратном обходе окружности ответ будет 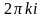. Интересно отметить, что результат получится не зависящим ни от ,ни от радиуса . Этот важный пример следует запомнить, так как дальше он будет использован в теореме.

15 Интегральная теорема Коши

Допустим, что аналитическая функция в замкнутой области , ограниченной кусочно-гладким контуром . Тогда действительная и мнимая части функции удовлетворяют в условиям КРЭД , причем, эти частные производные непрерывны в . Воспользовавшись равенством (1) параграф 13, мы видим, что эти условия полностью совпадают с условиями независимости криволинейных интегралов от пути интегрирования или, иначе говоря, оба интеграла по контуру равны нулю, т.е. Мы доказали следующую теорему Коши:

Теорема 1 Если функция аналитическая в замкнутой односвязной области, то интеграл от неё по границе области равен нулю.

В рассмотренных примерах 1 и 3 параграф 14 интегралы не равны нулю, что легко объяснить тем, что функции не аналитические в области, ограниченной контуром интегрирования. Равенство нулю интеграла по любому замкнутому контуру в некоторой области, очевидно, равносильно независимости интеграла от пути интегрирования и этой области.

Пусть теперь функция аналитическая в замкнутой многосвязной области , ограниченной внешним контуром и внутренними контурами 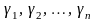. Мы проведем рассуждения только для случая двух внутренних контуров (Рисунок 23).

С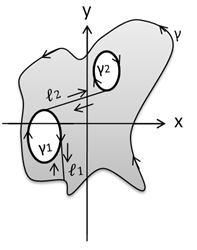 оединив поочередно контуры «бесконечно узкими каналами» (разрезами) мы превратим , в односвязную область, обход границы которой в положительном направлении показан стрелками. Тогда по теореме 1 интеграл по всей границе равен нулю. Но

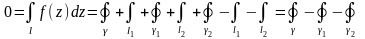
т.е. 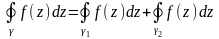. Обобщая это рассуждение на любое количество внутренних контуров, мы получим доказательство следующей теоремы:

Т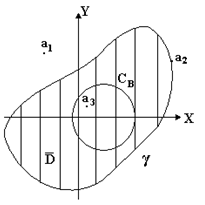 еорема 2 Если функция аналитическая в замкнутой многосвязной области, то интеграл от нее по внешнему контуру области равен сумме интегралов по всем внутренним контурам (предполагается, что интегралы берутся в одном, например, положительном направлении)

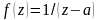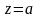П ример. Функция является аналитической на всей плоскости, кроме точки . Пусть – замкнутая кривая ограничивающая область .

Тогда: