Классический метод Рунге-Кутта

Метод Рунге-Кутта четвертого порядка получаем при

P=4, c₁=0, c₂= c₃=1/2, c₄=1, d₁=d₄=1/6, d₂=d₃=1/3

Расчетные формулы имеют вид:

; (i=1, 2, …, m) (9)

То есть берутся 4 направления и усредняются.

Для практической реализации погрешности решения можно применять правило Рунге, полагая P=4:

Программа решения дифференциального уравнения методом Рунге-Кутта:

program RungeKutta; {*** Mетод Рунге - Кутта ***}

var d,x,a,b,h,y,k1,k2,k3,k4:real;

m,i:integer;

function f(x,y: real): real;

begin f:=cos(x);

end;

BEGIN writeln('Введите значения концов отрезка [a,b]');

readln(a,b);

writeln('Введите начальное значение y0=y(x0)');readln(y);

writeln('Введите число значений функции на промежутке [a,b]');

read(m);

x:=a; h:=(b-a)/m;

for i:=0 to m do

begin writeln (x:10:3, y:15:4);

k1:=h*f(x,y);

k2:=h*f(x+h/2,y+k1/2);

k3:=h*f(x+h/2,y+k2/2);

k4:=h*f(x+h,y+k3);

d:=(k1+k2*2+k3*2+k4)/6; y:=y+d; x:=x+h

end; readln;

END.

Введите значения концов отрезка [a,b]

0 1.57

Введите начальное значение y0=y(x0)

0

Введите число значений функции на промежутке [a,b]

10

0.000 0.0000

0.157 0.1564

0.314 0.3089

0.471 0.4538

0.628 0.5875

0.785 0.7068

0.942 0.8087

1.099 0.8908

1.256 0.9509

1.413 0.9876

1.570 1.0000

Метод наименьших квадратов Постановка задачи

Пусть данные некоторого эксперимента представлены в виде таблицы:

xi	x1	x2	…	xn
yi	y1	y2	…	yn	(1)

П 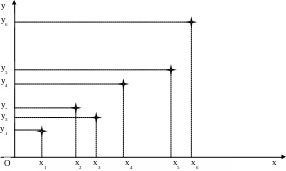оставим задачу об отыскании аналитической зависимости между x и y, т.е. некоторой формулы y=f(x). При этом потребуем, чтобы график искомой функции изменялся плавно и не слишком уклонялся от экспериментальных данных. Поиск такой зависимости называют «сглаживанием» экспериментальных данных. Формулу y=F(x) – эмпирической формулой или уравнением регрессии y на x.

Предположим, что приближающая функция y=F(x) имеет значения.

xi	x1	x2	…	xn
			…		(2)

Рассматривая совокупности (1) и (2) как координаты двух точек n-мерного пространства, найдем расстояние между ними по евклидовой метрике

Потребуем, чтобы эта величина была наименьшей. Это равносильно тому, что сумма квадратов должна быть наименьшей:

или

Тогда задача приближения функции f формулируется следующим образом: для функции f, заданной таблицей, найти функцию F определенного вида так, чтобы сумма квадратов была наименьшей.

Нахождение приближающей функции в виде линейной функции

Рассмотрим приближающую функцию в виде F(x,a,b) = ax+b.

Наша задача – отыскать значения параметров a и b.

Рассмотрим функцию или

Задача сводится к отысканию минимума функции Ф(a,b). Используем необходимое условие экстремума: ; .

Учитывая, что , , получим систему вида:

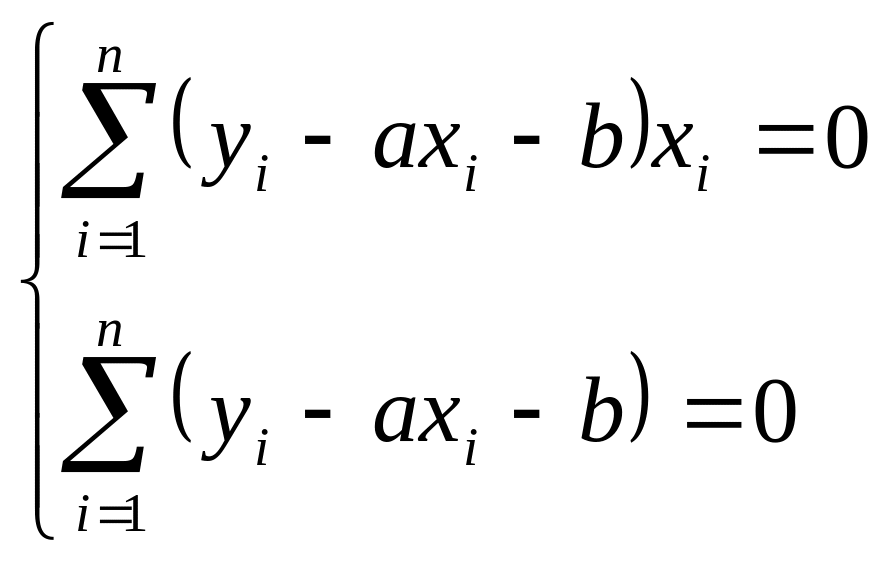
Далее, или

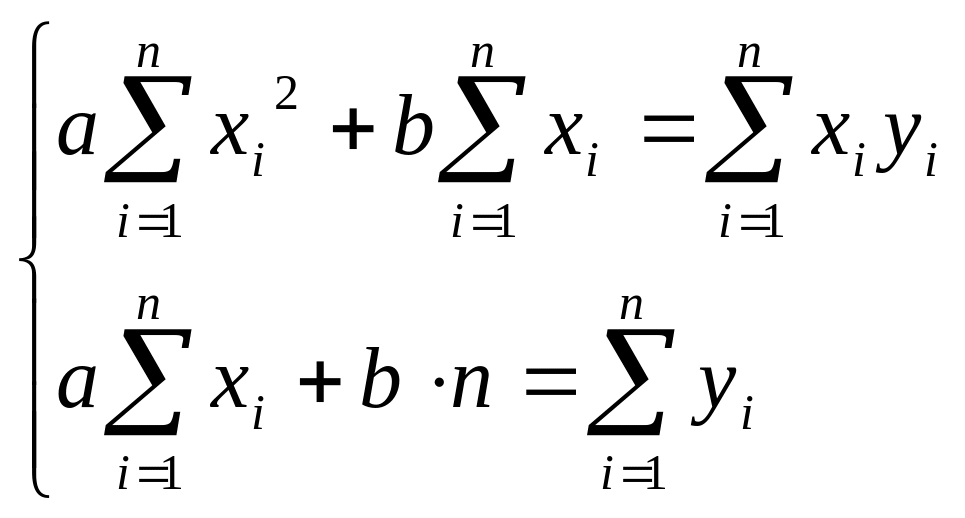
Выразим значения a и b из системы уравнений:

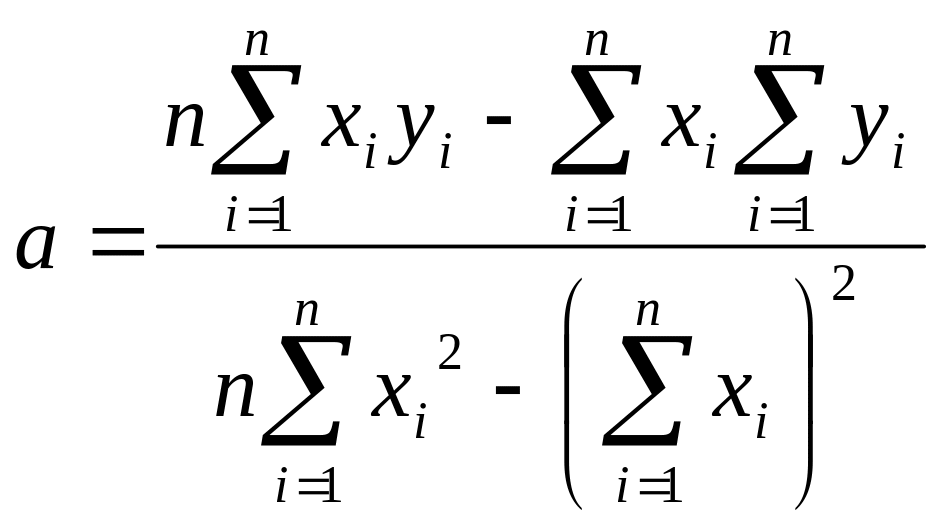
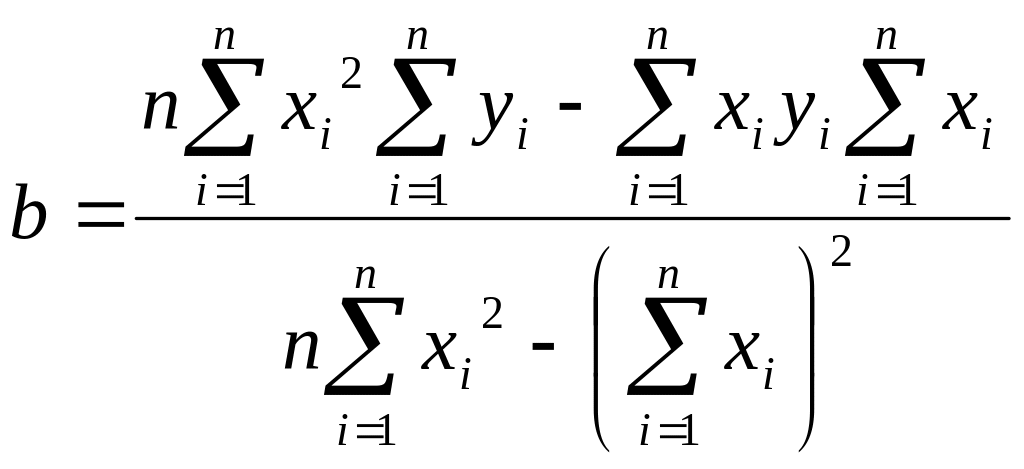
Существует показатель, характеризующий тесноту линейной связи между X и Y. Это (выборочный) коэффициент корреляции. Он вычисляется по формуле: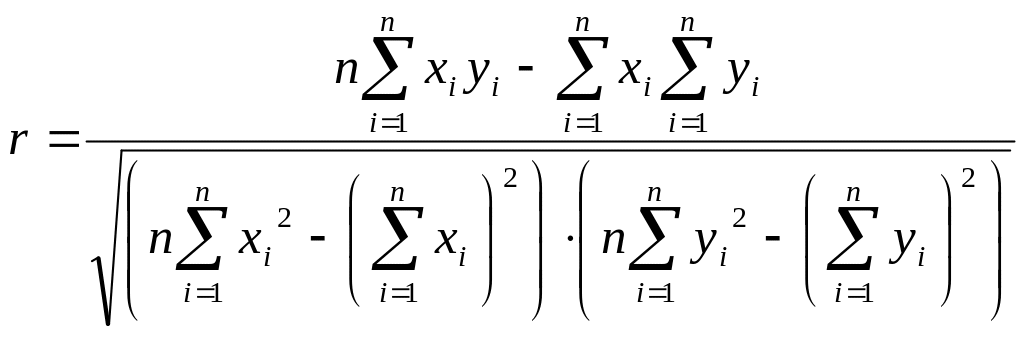

Значение коэффициента корреляции всегда удовлетворяет соотношению: -1r1. Чем меньше отличается абсолютная величина r от единицы, тем ближе к линии регрессии располагаются экспериментальные точки.

Если коэффициент корреляции равен нулю, то говорят, что переменные X и Y некоррелированы.