Метод Эйлера
В основе метода Эйлера лежит идея графического построения решения дифференциального уравнения, этот метод называется также методом ломаных Эйлера.
Угловой коэффициент
касательной к интегральной кривой в
точке M0(x0,y0)
равен
.
Найдем ординату y1 касательной, соответствующей абсциссе x1=x0+h.
Уравнение касательной
к кривой в точке M0
имеет вид
или
,
откуда y1=y0+hf(x0,y0).
Аналогично, угловой
коэффициент касательной к интегральной
кривой в точке M1(x1,y1)
равен
.
Точку M2(x2,y2)
получим соответственно
x2=x1+h y2=y1+hf(x1,y1).
Продолжая вычисления по данной схеме, получим формулы Эйлера для приближенного решения задачи Коши с начальными данными (x0,y0) на сетке отрезка [a, b] с шагом h:
xi=xi-1+h yi=yi-1+hf(xi-1,yi-1). (4)
Г
M4
M3
рафической
иллюстрацией приближенного решения
является ломаная, соединяющая
последовательно точки M0,
M1, …,Mm,
которую называют ломаной Эйлера.
M2
y
M1
M0
x
x0
x1
x2
x3
x4
O
Погрешность метода Эйлера можно оценить неравенством
,
(5)
которое можно
представить в виде d=Ch,
где
.
Таким образом, метод Эйлера имеет первый
порядок точности.
Практическую оценку погрешности решения, найденного на сетке с шагом h/2, в точке xi[a, b] производят с помощью приближенного равенства – правила Рунге:
(6)
где P – порядок точности численного метода.
Таким образом, оценка полученного результата по правилу Рунге вынуждает проводить вычисления дважды: с шагом h и h/2, причем совпадение десятичных знаков в полученных двумя способами результатах дает основание считать их верными.
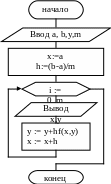
Программа решения дифференциального уравнения методом Эйлера
program Eiler;
var x,a,b,h,y:real;
m,i:integer;
function f(x,y: real): real;
begin f:=cos(x);
end;
begin writeln('Введите значения концов отрезка [a,b]');
readln(a,b);
writeln('Введите начальное значение y0=y(x0)');readln(y);
writeln('Введите число значений функции на промежутке [a,b]'); read(m);
x:=a; h:=(b-a)/m;
for i:=0 to m do
begin writeln (x:10:3, y:15:4);
y:=y+h*f(x,y); x:=x+h
end; readln;
end.
Блок-схема решения ДУ методом Эйлера |
Результаты выполнения программы |
|
Введите значения концов отрезка [a,b] 0 1.57 Введите начальное значение y0=y(x0) 0 Введите число значений функции на промежутке [a,b] 10 0.000 0.0000 0.157 0.1570 0.314 0.3121 0.471 0.4614 0.628 0.6013 0.785 0.7283 0.942 0.8394 1.099 0.9317 1.256 1.0031 1.413 1.0517 1.570 1.0764 |
Методы Рунге-Кутта
Численные методы решения задачи Коши , y(x0)=y0 на равномерной сетке {x0=a, x1, x2, …, xm=b} отрезка [a, b] с шагом являются методами Рунге-Кутта, если, начиная с данных y(x0)=y0 решение ведется по следующим рекуррентным формулам:
;
(i=1, 2, …, m) (7)
, 
Метод называют методом Рунге-Кутта порядка P, если от имеет P-й порядок точности по шагу h на сетке.
Метод Эйлера можно назвать методом Рунге-Кутта первого порядка.
Метод Рунге-Кутта второго порядка называют методом Эйлера-Коши, если P=2, c1=0, c2=1, d1=d2=1/2
; (i=1, 2, …, m) (8)
Для практической
реализации погрешности решения можно
применять правило Рунге, полагая P=2:
Программа решения дифференциального уравнения методом Эйлера-Коши:
program Eiler_Koshi;
var x,a,b,h,y,z:real;
m,i:integer;
function f(x,y: real): real;
begin f:=cos(x);
end;
begin writeln('Введите значения концов отрезка [a,b]');
readln(a,b);
writeln('Введите начальное значение y0=y(x0)');readln(y);
writeln('Введите число значений функции на промежутке [a,b]');
read(m);
x:=a; h:=(b-a)/m;
for i:=0 to m do
begin writeln (x:10:3, y:15:4);
z:=y+h*f(x,y);
y:=y+h*(f(x,y)+f(x+h,z))/2;
x:=x+h
end; readln;
end.
Введите значения концов отрезка [a,b]
0 1.57
Введите начальное значение y0=y(x0)
0
Введите число значений функции на промежутке [a,b]
10
0.000 0.0000
0.157 0.1560
0.314 0.3082
0.471 0.4528
0.628 0.5863
0.785 0.7054
0.942 0.8071
1.099 0.8889
1.256 0.9489
1.413 0.9855
1.570 0.9979