Математические модели и численные методы

Процесс решения задачи с использованием ЭВМ включает, как правило, следующие этапы:

1. Математическая постановка задачи и построение математической модели. На данном этапе требуется

• определить, что дано, что надо получить;

• выделить наиболее существенные свойства изучаемого объекта;

• установить между ними количественные соотношения;

Требования к математической модели:

• Математическая модель должна быть адекватной, т.е. правильно отражать действительность;

• Математическая модель не должна быть слишком сложной.

2. Алгоритмизация, т.е.

• Поиск метода решения задачи в рамках математической модели

• Разработка алгоритма (в виде словесного описания, математических формул, блок-схем).

3. Перевод алгоритма на язык программирования.

4. Исполнение программы на ЭВМ. В результате – получение результатов решения.

5. Анализ полученных результатов. Полученные результаты сравниваются с ожидаемыми, с данными, полученными экспериментальным путем.

Методы решения задачи делятся на

Точные: аналитические графические

Приближенные аналитические графические численные

Структура погрешности при решении задачи на эвм

Погрешность возникает на ряде этапов решения задачи. Введем обозначения:

R – точное решение задачи (результат);

– приближенное решение задачи;

ε – полная погрешность.

Полная погрешность включает в себя:

• Погрешность исходных данных и математической модели. Возникает по причине неточности исходных данных и несоответствия построенной математической модели реальной ситуации. Таким образом, будет получен результат R₁≠R.

ε₁ – неустранимая погрешность.

• Погрешность метода. Возникает, если выбран приближенный (например, численный) метод. Таким образом, будет получен результат R₂≠R₁.

ε₂ – устранимая погрешность.

• Погрешность вычислений: .

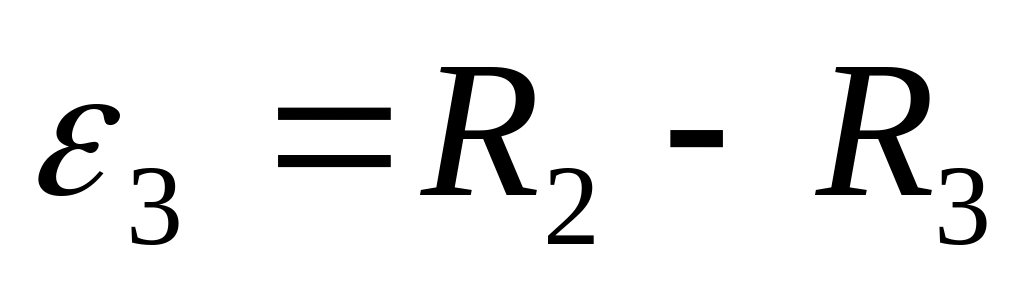Таким образом, полная погрешность:

Решение уравнений с одной переменной Постановка задачи

Рассмотрим уравнение вида F(x)=0, где F(x) – определенная и непрерывная на отрезке [a,b] функция.

Корнем уравнения F(x)=0 называется такое значение x^*, которое обращает уравнение в верное равенство.

x^* - корень уравнения F(x)=0  x^* - нуль функции y=F(x).

Решить уравнение – значит установить, имеет ли оно корни, сколько корней, и найти их значения с заданной степенью точности.

Нахождение корней уравнения состоит из двух этапов:

1. Отделение корней – выделение промежутков, содержащих ровно 1 корень.

2. Уточнение корней – нахождение корней с заданной степенью точности.

Отделение корней

Отделение корней может осуществляться графически или программным путем.

I. Графический способ отделения корней

а) Теорема.

Е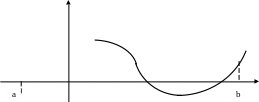 сли на отрезке [a,b] функция y=F(x) определена и непрерывна, и на его концах принимает значения разных знаков (т.е. F(a)F(b)<0), то уравнение F(x)=0 имеет на этом отрезке, по крайней мере, один корень.

Е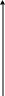 сли функция y=F(x) на отрезке [a,b] строго монотонна, то корень единственный.

b

a

Требуется указать отрезок, содержащий нуль функции.

Н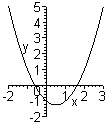 апример, пусть требуется отделить корни уравнения x²-x-1=0. Построим график функции y=x²-x-1 и укажем отрезки, содержащие точки пересечения графика функции с осью абсцисс.

Искомые промежутки: [-1; 0] [1; 2].

б) Иногда проще рассмотреть вместо уравнения y=F(x) равносильное ему уравнение f₁(x)=f₂(x). В этом случае требуется указать отрезок, содержащий абсциссу точки пересечения графиков функций y=f₁(x) и y=f₂(x).

Н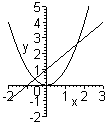 апример, пусть требуется отделить корни уравнения x²-x-1=0. Рассмотрим равносильное ему уравнение x²=x+1. Тогда вместо отрезков, содержащих точки пересечения графика функции y=x²-x-1 с осью абсцисс, можно указать отрезки, содержащие точки пересечения графиков функций f₁(x)=x² и f₂(x)=x+1.

Искомые промежутки: [-2; 0] [1; 3].