Решение системы линейных алгебраических Постановка задачи

Рассмотрим систему m линейных уравнений с n неизвестными:

Ее можно записать в матричном виде A x = B, где

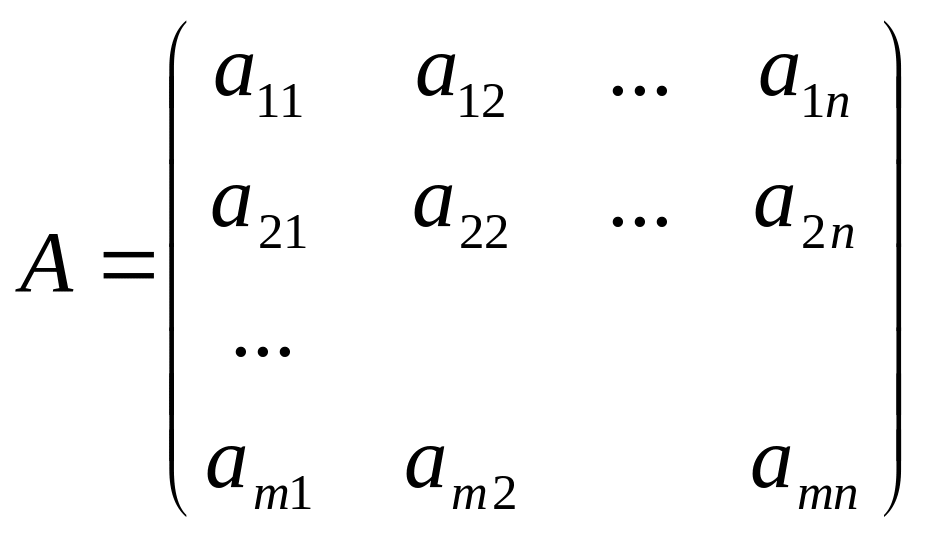
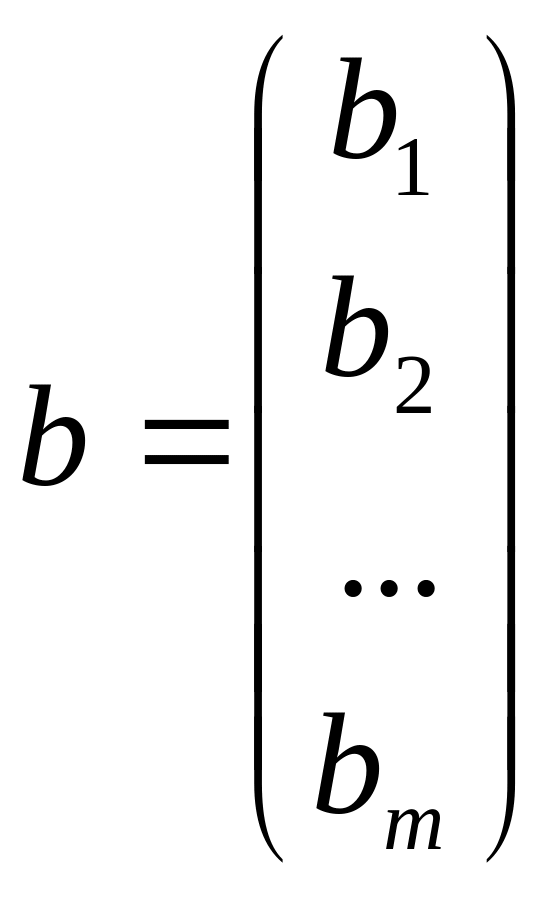
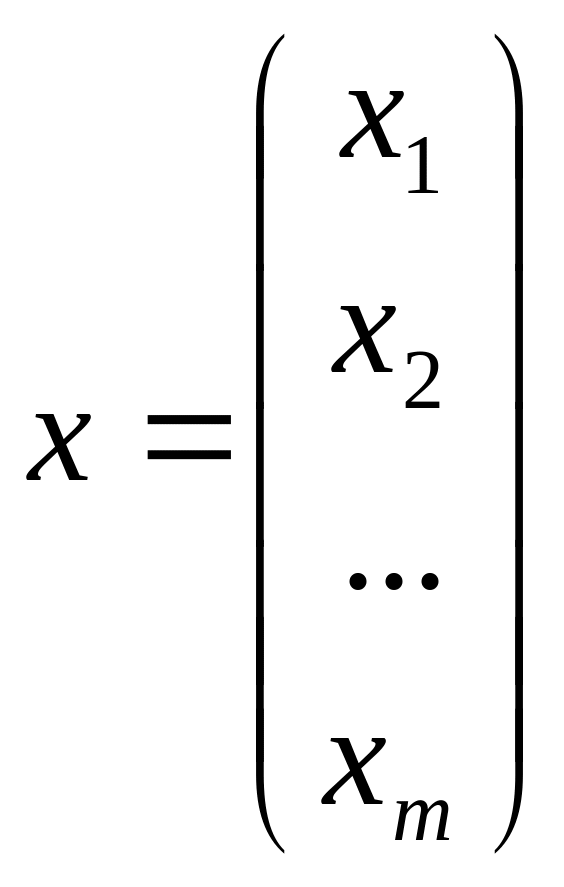
Решить СЛУ – значит найти набор таких чисел , которые превращают уравнения в верные равенства.

СЛУ совместна, если она имеет хотя бы одно решение.

СЛУ несовместна (противоречива), если она не имеет решения.

Совместная СЛУ определенна, если она имеет единственное решение и неопределенна, если более одного решения.

СЛУ имеет единственное решение, если ранг матрицы A равен рангу расширенной матрицы (A|b): rang(A) = rang(A|b).

СЛУ имеет единственное решение, если rang(A) = n и бесконечно много решений, если rang(A) < n.

Если матрица A – квадратная и det(A)0, то она называется невырожденной.

СЛУ с n неизвестными, имеющими невырожденную матрицу A, совместна и имеет единственное решение.

Единичной матрицей E называется квадратная матрица, у которой на главной диагонали стоят единицы, а на остальных местах – нули.

Обратной матрицей по отношению к матрице A называется такая матрица A^-1, что A A^-1=A^-1 A = E.

Матрица A^T, полученная перестановкой в матрице A строк со столбцами, называется транспонированной.

Квадратная матрица симметрична, если A=A^T.

Все численные методы решения СЛУ можно разделить на прямые, итерационные и вероятностные.

Прямые методы дают решение системы за конечное число арифметических операций.

Например, метод Крамера (метод определителей),

метод Гаусса (метод последовательного исключения неизвестных).

«Плюсы»	«Минусы»
Просты Универсальны Не требуют приведения к определенному виду	Достаточно громоздкие вычисления

Итерационные методы дают решение системы как предел последовательности приближений, вычисляемых по единообразной схеме.

Например, метод простой итерации,

метод Зейделя.

«Плюсы»	«Минусы»
Требуют мало места в памяти Самоисправляющиеся методы	Требуют приведения к определенному виду

Вероятностные методы носят общее название – методы Монте-Карло.

Пусть получено решение СЛУ: . Рассматривается вектор невязки . Если велико, то где-то допущена ошибка, если мало, то ошибка отсутствует.

Метод Гаусса

Метод Гаусса относится к точным методам, однако вычислительная ошибка присутствует всегда (ошибка округления и, возможно, ошибка исходных данных).

Рассмотрим систему m линейных уравнений с n неизвестными:

Алгоритм состоит из двух этапов.

I. Прямой ход – приведение матрицы к треугольному виду (сверху вниз):

II. Обратный ход – определение неизвестных (снизу вверх).

Ручные вычисления по схеме единственного деления оформляют в виде таблицы с контролем вычислений, для чего в таблицу включены

• столбец контрольных сумм ,

• столбец сточных сумм S.

Контроль в прямом ходе:

• После внесения коэффициентов при неизвестных и свободных членов исходной системы находят контрольные суммы (суммы коэффициентов и свободных членов по строкам) и вносят их в столбец .

• Далее, выполняя преобразования, над контрольными суммами производятся те же преобразования, что и над свободными членами.

• После выполнения каждого преобразования находят строчную сумму результатов и помещают ее в столбец S.

• При отсутствии вычислительных ошибок числа в столбцах  и S должны практически совпадать.

Контроль в обратном ходе:

При безошибочном выполнении вычислений в столбце  должны быть на единицу больше соответствующих значений неизвестных из столбца свободных членов

Рассмотрим примеры решения СЛУ методом Гаусса

Разделы	x1	x2	x3	св чл	сумма	S
	3,25	14,52	-1,32	367,58	384,03
	32,02	-4,36	5,73	516,91	550,3
А	7,21	11,92	-41,46	-886,32	-908,65
	1	4,4677	-0,4062	113,1015	118,1631	118,163
	0	-147,4158	18,7365	-3104,6000	-3233,2825	-3233,2793
	0	-20,2921	-38,5313	-1701,7818	-1760,606	-1760,6052
А1		1	-0,1271	21,0602	21,9331	21,9331
		0	-41,1104	-1274,4261	-1315,5373	-1315,5365
А2			1	31,0001	32,0001	32,0001
			1	31,0001	32,0001
В		1	0	25,0003	26,0003
	1	0	0	13,9999	15

Невязки	e1=	367,58	-	367,583899	=	-0,003899
	e2=	516,91	-	516,906063	=	0,003937
	e3=	-886,32	-	-886,321291	=	0,001291