2. Определение объема выборки в случае непрерывных переменных

Пусть это среднее значение наблюдений при простой случайной выборке, необходимо чтобы отклонение (разница) между выборочной и генеральной средней с небольшим риском α было больше выбранного предельного значения ошибки

где d – предельное значение ошибки оценки .

Предположим, что распределено нормально. В этом случае его стандартная ошибка будет определяться по формуле:

Формула, которая будет связывать объем выборки с желательной степенью точности, будет иметь следующий вид:

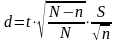
Первоначально определяем объем выборки в качестве первого приближения:

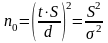
Если по результатам первого приближения отношение 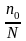достаточно мало, то n будет определяться по формуле , в противном случае объем выборки будет определяться вторым приближением по следующей формуле:

При оценке суммарного значения для совокупности с предельной ошибкой d объем выборки в качестве первого приближения можно определить по следующей формуле:

Далее проводят те же рассуждения о возможности определения объема выборки n, если отношение приблизительно мало или велико. В случае, если это отношение значительно, то объем выборки n так же определяется по указанной выше формуле.

3. Определение объема выборки при оценивании долей и процентов

При условном значении предельной ошибки d оценки доли р единиц класса С необходимо соблюдение следующего условия:

d – предельное значение ошибки значения р;

Предполагая, что производится простой случайный отбор и выборочная доля р имеет нормальное распределение :

Формула, которая связывает объем выборки n с желательной степенью точности:

t – значение абсциссы для кривой нормального распределения, отсекающее «на хвостах» площадь α

(на хвостах по 15,85%)

t=1

(на хвостах по 2,3%)

t=2

(на хвостах по 0,15%)

t=3

Объем выборки n отсюда рассчитывается по следующей формуле:

Для практического применения данной формулы вместо Р можно подставить предварительную оценку р. Если объем совокупности N достаточно велик, то сначала можно приблизительно рассчитать объем выборки на основе следующей формулы:

Где – желательная дисперсия выборочной доли.

Если отношение довольно мало, то будет удовлетворительным приближением для n.

В противном случае объем выборки на основе первого приближения можно определить по следующей формуле:

Формула для определения используется и в том случае, если величины d, p и q выражены не в долях единиц, а в процентах. Поскольку произведение pq растет, когда р → Ѕ (50%). Более надежная оценка выборки n будет иметь в том случае, если в интервале, где как предполагалось находится Р, принять в качестве р ближайшее в Ѕ число.

5. Простой случайный отбор.

Формирование простой случайной выборки. Алгоритм извлечения простой случайной выборки. Оценка параметров простой выборочной совокупности: суммарного значения, среднего значения, дисперсии, стандартной ошибки по выборке, определение доверительных границ.